基于碳排放的車輛路徑優化和速度優化

孫金枝

摘要：近年來，環境和能源問題成為人們關注的一個焦點。交通運輸業是一個高能耗的行業，該行業實現節能減排是有必要的。文章以降低車輛碳排放為目標進行車輛路徑構建和速度優化，從而實現交通運輸業的節能減排。在考慮配送節點約束、車輛速度約束、容量約束、時間窗約束的情況下，構建了一個非線性數學模型，并設計了一個兩階段算法：第一階段假設網絡速度相同進行路徑優化，第二階段在已知路徑的情況下進行速度優化。最后通過算例驗證了算法的可行性和有效性。

關鍵詞：帶時間窗的車輛路徑問題;速度優化;碳排放

中圖分類號：U116.2文獻標識碼：A

O引言

隨著環境污染、能源枯竭問題越來越突出，人們也更加關注環境和能源問題。交通運輸業是一個高能耗的行業，《公路水路交通節能中長期規劃綱要》、《“十三五”現代綜合交通運輸體系發展規劃》等都指出要降低能源消耗，減少污染氣體的排放。除了構建合理的交通運輸系統、研發新能源汽車等措施外，交通運輸企業可以通過構建合理的車輛行駛路徑、車輛行駛速度等措施來降低能源消耗。基于此確定了本文的研究主題——基于碳排放的車輛路徑優化和速度優化。

關于路徑優化（VRP）的文章很多，研究也相對成熟。本文主要關注了帶時間窗的車輛路徑問題（VRFTW），該類問題屬于典型的NP-hard問題，求解方式包括精確算法和啟發式算法。精確算法有分支定界、列生成等，Desrochers等用分支定界算法解決列生成中的子問題，該算法可以求得VRPTW的最優解。Choi等采用列生成算法求解整數規劃問題，并針對VRPTW提出了兩種動態規劃算法。啟發式算法有禁忌搜索、蟻群算法等，Pisinger等提出了大規模領域搜索算法框架來解決VRPTW的問題。張金金（2012）設計了兩階段的啟發式算法，何小鋒，馬良（2013）通過將量子計算和蟻群算法相結合提出了量子蟻群算法。

速度優化問題最先出現在航海路徑減排問題上。Fagerholt等證明了速度優化問題為非線性凸規化問題。Norstad等提出了一個遞歸算法來求解固定路徑上的速度優化問題，被Hvattum等證明該算法是精確算法。

目前，考慮碳排放的路徑優化問題還比較少。BektaS等提出了污染路徑問題并建立了一個非線性數學模型，然后通過離散化速度，將非線性模型轉化為線性模型進行求解。Fukasawa等構建混合整數規劃算法解決PRP問題。Demir等建立了一個ALNP算法解決污染路徑問題。李進等以旅行時間、碳排放和油耗的總費用最小化為目標函數，設計了兩階段啟發式算法。

本文在配送成本中考慮車輛油耗成本和車輛使用成本，以路徑優化和速度優化為決策變量建立了數學模型，并設計了一個兩階段算法來解決該問題，第一階段假設網絡速度相同采用二分法求解可能路徑，第二階段在已知的路徑集合中進行速度優化，從而輸出最優解。

1問題描述與模型構建

1.1問題描述

根據1.2.1，該目標函數為凸函數，約束式（13）為非線性約束，該問題為非線性凸規劃問題，速度決策可以借助MAT-LAB的fmincon命令求解。

2.2算法設計

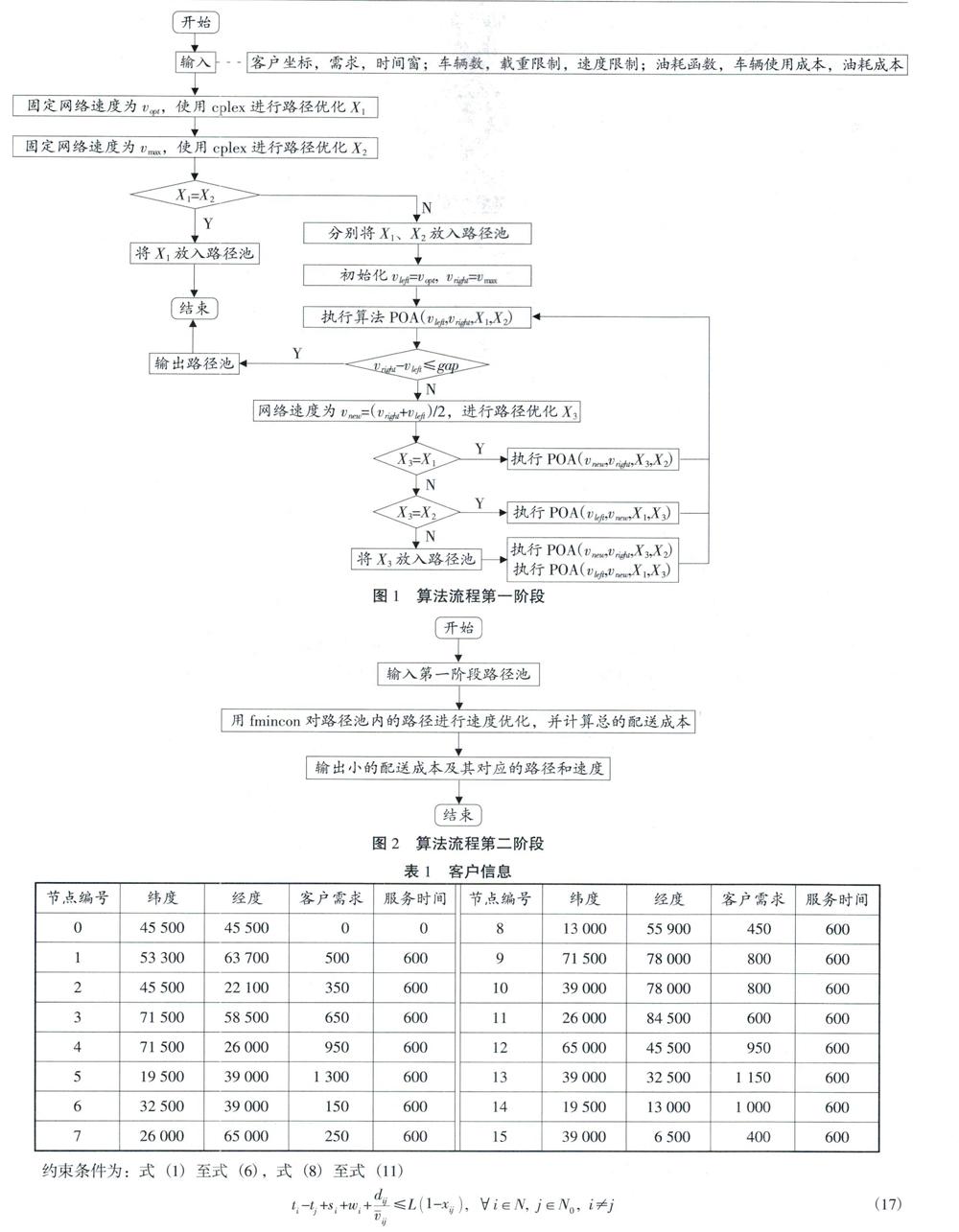
本算法設計整體思路分為兩個階段，第一階段是假定網絡速度相同的情況下，對網絡進行路徑優化;第二階段是在獲得路徑之后，對路徑上的速度進行速度優化。由于給定的網絡速度會影響求解結果。本文在第一階段用二分法求出所有可能路徑，之后在第二階段對所有路徑進行速度優化，從而輸出最優解。具體算法流程如圖1、圖2所示。

3算例分析

3.1參數設置

現有一個配送中心和15個客戶，所有節點的經緯度、客戶需求（單位kg）、需要的服務時間（單位s）如表1所示。此外，配送中心有載重量為3.5t的車輛10輛，采用的油耗成本如1.2.2中所示，車輛最高限速為120km/h，最低限速為20km/h，最優速度υ_opt為63.39km/h。單位里程的油耗成本C₁=7.5，車輛使用成本C₂=100。對于不同的測試實例，生成不同寬度的時間窗。

3.2算法有效性驗證

原模型是非線性混合整數規劃，不容易求得最優解。為此，需要尋找原問題最優解的下界。假設（x，y）是原問題P1的最優解，問題P2仍然按照該路徑和速度行駛，也可以滿足所有約束，因此（x，y）也是問題P2的可行解。則P2的最優值小于等于P1的最優值，因此問題P2的最優值可以作為問題P1最優值的下界。

3.3固定速度和本文算法計算結果比較

為了進一步說明對車輛進行速度優化的必要性，將網絡速度固定為使單位里程油耗最小的速度υ_opt=63.39km/h，計算了在此情況下的配送成本、車輛使用數量，如表3所示。計算結果表明，對車輛進行速度優化，平均可以節省11.98%的費用，因此對車輛進行速度優化是有必要的。

4結束語

本文以車輛油耗成本和使用成本為目標函數，建立了以路徑和速度同為決策變量的數學模型，并針對模型設計了算法，通過算例驗證了模型和算法的可行性和有效性。但是本文選用cplex進行路徑優化，僅適用于客戶規模較小的情況，在后續研究中將針對大規模客戶進行研究。