巧解“一元一次方程”

徐未君 青海師范大學數學與統計學院 青海西寧 810000

法國數學家笛卡爾說：一切問題都可以轉化為數學問題，一切數學問題都可以轉化為代數問題，而一切代數問題又都可以轉化為方程問題！雖然笛卡爾的設想未能實現，但是也充分說明了方程的重要性。方程是刻畫現實世界的有效數學模型，一元一次方程是方程中最簡單、最基礎的部分，在數學學習中，要注意解題技巧的積累。本文介紹了幾種一元一次方程的解題技巧。

一、裂相相消法

將方程中的每一項分解成兩項，然后重新組合，消去一些相同項，達到簡便求和的目的。

例1.解方程：

解析：上述方程的每一項都可以拆分成兩個式子相減的結果，我們把每個式子拆分后，然后相加，就得到這樣一個式子：

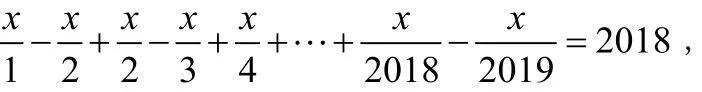
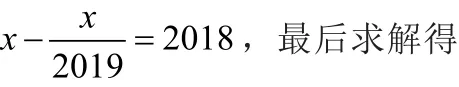
二、巧用“1”的關系

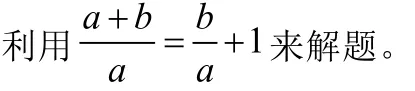
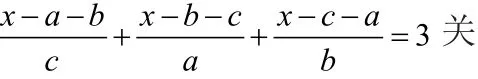
三、局部通分法：

通過觀察等式兩邊，把有公倍數的分母的式子放在一起，進行通分，或者是帶小數的方程，進行每項化簡，以便于簡便運算。

例4. 解方程：

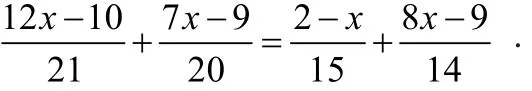
四、整體通分法：

整體對方程的左右兩邊進行通分，如果等式兩邊是兩個單項式，繼續移項，使之左邊兩邊分別為兩個整體。

五、提取公因式法：

找出每一項的公因式，提取公因式后，進行合并，計算求解。

上述五種方法是在解一元一次方程時用到的重要的方法，數學題目的解題思路都是相通的，同學們要學會融會貫通，在以后的學習中，不斷總結新的方法，提高學習效率。同時，掌握好一元一次方程，也為后續學習一元二次方程、一元一次不等式、二元一次方程等內容做鋪墊。