一種基于廣域測量信息的在線同調分群方法

張艷霞 尹佳鑫 蒙高鵬 李杰 李多多

Abstract：In order to identify coherent generator groups quickly and accurately， two clustering indexes based on wide area measurement information are proposed. Firstly， the result of the pregrouping could be attained by calculating the effective values of the power angle difference among all the generators. Then， a similarity measure method called ρHsim was constructed by combining the Pearson correlation coefficient and the Hsim function. It considered the distance difference and the trend difference of the generator power angle trajectories at the same time， which can be applied to attain the result of furthergrouping. An improved clustering algorithm combining quality threshold （QT） clustering and kmeans clustering was proposed to meet the requirements of online recognition of coherent generators. The effectiveness of the proposed method is verified by the EPRI36 node system simulation example. Analytical results show that the generators with large power angle difference can be quickly assigned to different groups in the pregrouping stage by using the effective values of the power angle difference. In the furthergrouping stage， the result of coherency identification at different scales and levels of detail can be attained by using the new similarity measure index ρHsim.

Keywords：wide area measurement system; coherency identification; effective values of the power angle difference; correlation coefficient; Hsim function; quality threshold clustering; kmeans clustering

0 引 言

為了提高對大規模電力系統動態過程的分析效率，需采取有效方法對電網進行簡化計算。目前對復雜電力網絡的動態行為進行分析一般采用動態等值進行簡化計算[1-3]。而應用最廣泛的動態等值方法是發電機的同調等值法，該方法通過識別電力系統受到擾動后轉子搖擺曲線相似的發電機，將其聚合成一臺等值機，從而有效地簡化系統，減少電力系統動態分析的計算量。此外，系統發生失步振蕩時，解列控制技術是保障電力系統安全可靠運行的重要手段，而其前提就是準確快速地識別同調機群[4-5]。

同調識別的方法有很多，大體上可以分為基于模型參數的方法和基于發電機功角曲線的數據挖掘法。基于模型參數的方法主要包括電氣距離法、狀態空間法、慢同調法等。文獻[6]引入電氣距離衡量發電機間的緊密程度，并將其作為同調發電機的分群指標。文獻[7]直接對系統的狀態矩陣進行分析，進而給出了識別同調機群的方法。文獻[8]通過構建系統的線性化模型，進而提出基于慢同調理論的發電機同調分群方法。以上方法都受系統模型精度的影響，通常難以應用于大型的電力系統，也無法考慮系統運行狀態以及故障類型對同調分群的影響。

隨著廣域測量系統（wide area measurement system，WAMS）的出現和通信技術的發展，發電機動態受擾軌跡的獲得變得容易，為基于發電機功角曲線的同調識別提供了數據支持，使得基于發電機功角曲線的數據挖掘方法得到了蓬勃發展。文獻[9]利用非負矩陣分解算法對發電機角速度數據進行降維，進而通過聚類實現發電機同調分群。文獻[10]利用小波分解提取發電機功角搖擺曲線的低頻信息，進而根據小波相位差進行發電機同調分群。文獻[11]利用通信領域的軌跡特征提取方法分析發電機的擾動軌跡，提出了用各發電機功角曲線之間的結構差異度作為同調分群標準的新方法。這些方法的應用對同調識別的準確性有較大提升，但仍存在計算復雜、識別時間較長等缺點。

本文提出了兩種基于廣域測量信息的同調分群指標。發電機功角差有效值指標可以迅速地對功角擺開差異較大的發電機組進行分群。結合皮爾森相關系數和Hsim函數構造的相似度度量指標ρHsim，同時考慮了曲線間距離和走勢差異，可以對發電機進行更有效地劃分。本文在再分群階段還采用了屬性閾值（quality threshold，QT）聚類和kmeans聚類相結合的改進聚類算法實現分群計算。

1 基于廣域測量信息的同調分群指標

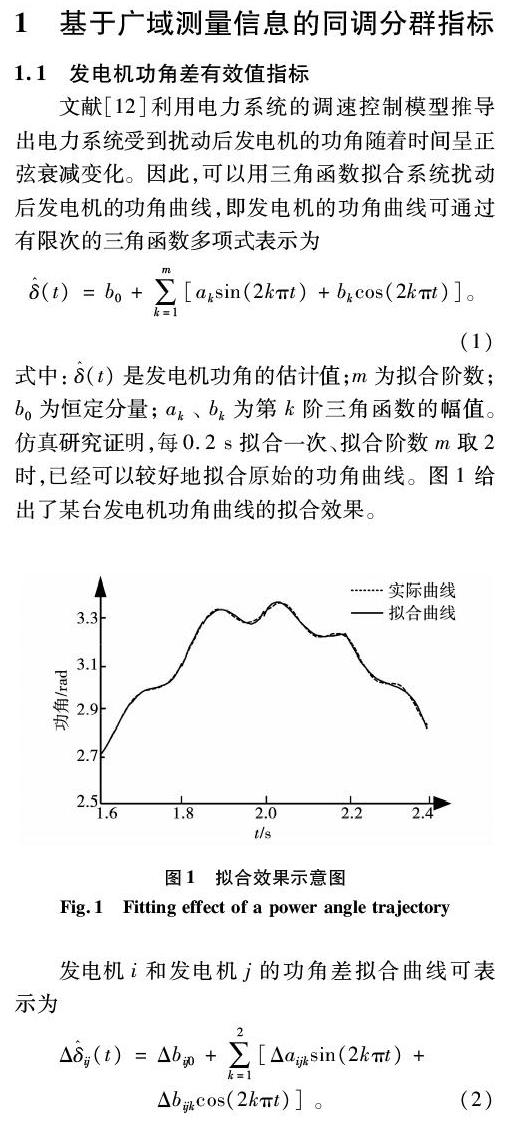
1.1 發電機功角差有效值指標

2 QT聚類與k-means聚類的結合算法 ?為了再分群階段的求解需要，本文采用了QT聚類與k-means聚類相結合的算法。

QT聚類是為基因聚類而提出的一種原理簡單的聚類方法[15]。其基本思路為：首先以樣本集合中的每一個樣本為初始聚類中心，將所有與之相似度指標大于閾值T的樣本合并至該類，形成若干個相互重疊的簇。然后選擇其中包含樣本數最多的簇作為第一類，并從樣本集合中移除該類所有樣本。剩下的樣本繼續執行上述過程，直到所有的樣本完成歸類。

QT聚類通過限定相似度閾值T，將差異度較大的樣本作為不同類的聚類中心分離出來。但是，對于那些與多個聚類中心的相似度都大于閾值的樣本處理不夠精確。因此，QT聚類單獨使用精確度不高，但其可以作為更加精細聚類算法的初始計算步驟。

k-means算法是目前應用最廣泛的聚類算法，其基本思路為：首先隨機地確定k個初始聚類中心，并將其他樣本直接劃分到與其相似度最高的聚類中心。然后重新計算每個類的中心，并不斷重復這一過程直到滿足收斂要求。

k-means聚類原理簡單并且高效，通過不斷地對聚類中心進行優化，使得每一次改進之后獲得的分組方案都比上一次好。但是單純使用k-means算法存在很大的局限性，主要是在數據聚類前很難確定聚類的個數k，且k-means算法對初始的聚類中心十分敏感[16-18]。這兩個缺陷，限制了k-means算法的應用。

本文將QT聚類與k-means聚類相結合，在k-means聚類前先用QT聚類算法來解決聚類個數k和聚類中心問題，即人為設定相似度閾值T，利用QT聚類直接得到k個類及其各個類的聚類中心。以此作為k-means的初始聚類中心，再通過k-means算法實現最終的聚類分群。應用該算法進行同調分群的具體實現過程以及用到的公式在下節中給出。

QT和k-means結合聚類算法具有以下特點。其一，只需人為確定相似度閾值T這一個參數，該參數物理意義清晰，容易設置。其二，一旦T確定，分群結果就是唯一的，不需要考慮數據的排列順序。其三，傳統k-means算法每次迭代過程都需要重新計算聚類中心，處理高維數據時計算量極大，而本文提出了平均相似度的概念，極大地簡化了聚類中心的計算。其四，結合算法既具有QT聚類的實用性，又具有k-means聚類的準確性。

與其他運用聚類算法的分群方法相比，本文的結合聚類算法具有一定優勢。文獻[9]利用了k-means算法，但如果初始聚類中心選擇不當會造成迭代次數增多甚至達不到最優聚類效果;文獻[11]采用了層次聚類算法，不存在初始聚類中心選取的問題，但聚類速度不如k-means算法。本文的結合聚類算法利用QT聚類選出的初始聚類中心可以保證k-means算法用較少的迭代次數達到最優聚類效果。因此，文獻[11]的層次聚類算法、文獻[9]的k-means聚類算法以及本文的改進聚類算法，在計算效率上是依次遞增的。

3 同調分群步驟及流程

設待研究的電力系統中有M臺發電機，每臺發電機都裝有PMU，則預分群的步驟如下：

1）以0.2 s為擬合周期對各發電機的功角采樣數據進行三角函數擬合。

5 結 論

1） 本文同調分群方法基于WAMS實測的發電機功角軌跡，因此它不受系統模型精度的影響，并且適用于各種運行狀態和故障類型。

2）本文提出的同調分群指標綜合考慮了發電機功角軌跡間的距離和走勢差異，物理意義清晰。

3）本文將QT聚類與k-means聚類相結合形成了一種新的實用高效的聚類方法。該算法只需人為設定一個參數，物理意義清晰，容易設置，可以根據分群的精度要求對發電機組進行同調分群。

4）本文提出的分群算法，計算量不大，易于實現，每隔0.2 s能給出一次分群結果，適合在線同調分群。

參 考 文 獻：

[1] 倪敬敏，沈沉，譚偉，等.一種基于非平衡點處線性化的同調識別方法[J].電力系統自動化，2010，34（20）：7.

NI Jingmin，SHEN Chen，TAN Wei，et al.A coherence identifying method based on linearization at non-equilibrium point[J].Automation of Electric Power Systems，2010，34（20）：7.

[2] 譚偉，張雪敏，沈沉.新的同調識別方法及其在切機算法中的應用[J].西南交通大學學報，2009，44（4）：507.

TAN Wei，ZHANG Xuemin，SHEN Chen.New coherency identification approach and its application to generator tripping algorithm[J].Journal of Southwest Jiaotong University，2009，44（4）：507.

[3] AGHAMOHAMMADI M R，TABANDEH S M.A new approach for online coherency identification in power systems based on correlation characteristics of generators rotor oscillations[J].International Journal of Electrical Power and Energy Systems，2016，83：470.

[4] 文俊，劉天琪，李興源，等.在線識別同調機群的優化支持向量機算法[J].中國電機工程學報，2008，28（25）：80.

WEN Jun，LIU Tianqi，LI Xingyuan，et al.Online identification of coherent generator using optimized LS-SVM[J].Proceedings of the CSEE，2008，28（25）：80.

[5] 董超，廖清芬，唐飛，等.基于Teager能量算子的低頻振蕩節點同調分群[J].電網技術，2012，36（5）：263.

DONG Chao，LIAO Qingfen，TANG Fei，et al. Teager energy operator based coherent node grouping for power system low-frequency oscillation[J]. Power System Technology，2012，36（5）：263.

[6] 廖庭堅，劉光曄，雷強，等.計及電動機負荷的電力系統動態等值分析[J].電網技術，2016，40（5）：1442.

LIAO Tingjian，LIU Guangye，LEI Qiang，et al.Analysis of dynamic equivalence with consideration of motor loads in power systems[J].Power System Technology，2016，40（5）：1442.

[7] 趙書強，常鮮戎，潘云江.電力系統同調機群識別的一種模糊聚類方法[J].電網技術，2001，25（4）：10.

ZHAO Shuqiang，CHANG Xianrong，PAN Yunjiang.A fuzzy clustering method for coherent generator groups recognition in power system[J]. Power System Technology，2001，25（4）：10.

[8] 宋洪磊，吳俊勇，冀魯豫.基于慢同調理論和希爾伯特-黃變換的發電機在線同調識別[J].電力自動化設備，2013，33（8）：70.

SONG Honglei，WU Junyong，JI Luyu.Online identification of coherent generators based on slow coherency theory and Hilbert-Huang transform[J]. Electric Power Automation Equipment，2013，33（8）：70.

[9] 吳興揚，衛志農，孫國強，等.基于非負矩陣分解的同調機群識別方法[J].電力系統自動化，2013，37（14）：59.

WU Xingyang，WEI Zhinong，SUN Guoqiang，et al.A method for identifying coherent generators based on non-negative matrix factorization[J].Automation of Electic Power System，2013，37（14）：59.

[10] AVDAKOVIC S，BECIROVIC E，NUHANOVIC A，et al.Generator coherency using the wavelet phase difference approach[J] .IEEE Transactions on Power Systems，2014，29（1） ：271 .

[11] 張亞洲，張艷霞，蒙高鵬，等.基于廣域信息的同調機群聚類識別方法[J].電網技術，2015，39（10）：2889.

ZHANG Yazhou，ZHANG Yanxia，MENG Gaopeng，et al.A wide area information based clustering recognition method of coherent generators[J].Power System Technology，2015，39（10）：2889.

[12] 宋方方，畢天姝，楊奇遜.基于WAMS的電力系統受擾軌跡預測[J].電力系統自動化，2006，30（23）：27.

SONG Fangfang，BI Tianshu，YANG Qixun.Perturbed trajectory prediction method based on wide area measurement systems[J].Automation of Electric Power Systems，2006，30（23）：27.

[13] 楊風召，朱揚勇.一種有效的量化交易數據相似性搜索方法[J].計算機研究與發展，2004，41（2）：361.

YANG Fengzhao，ZHU Yangyong.An efficient method for similarity search on quantitative transaction data[J].Journal of Computer Research and Development，2004，41（2）：361.

[14] 宋智超，康健，孫廣路，等.特征選擇方法中三種度量的比較研究[J] .哈爾濱理工大學學報，2018，23（1） ：111.

SONG Zhichao，KANG Jian，SUN Guanglu，et al.The comparison of three measures in feature selection[J] .Journal of Harbin University of Science and Technology，2018，23（1） ：111.

[15] 黃旭，呂強，錢培德.一種用于蛋白質結構聚類的聚類中心選擇算法[J].自動化學報，2011，37（6）：682.

HUANG Xu，L Qiang，QIAN Peide.An exemplar selection algorithm for protein structures clustering[J].Acta Automatica Sinica，2011，37（6）：682.

[16] 王勇，唐靖，饒勤菲，等.高效率的K-means最佳聚類數確定算法[J].計算機應用，2014，34（5）：1331.

WANG Yong，TANG Jing，RAO Qinfei，et al.High efficient K-means algorithm for determining optimal number of clusters[J].Journal of Computer Applications，2014，34（5）：1331.

[17] 朱紅霞，沈炯，李益國.基于滿意模糊聚類的熱工過程多模型建模方法[J] .電機與控制學報，2016，20（10）：94.

ZHU Hongxia，SHEN Jiong，LI Yiguo.Satisfactory fuzzy clustering-based multi-model modeling method for thermal process[J].Electric Machines and Control，2016，20（10）：94.

[18] 牛培峰，劉超，李國強，等.基于雙層聚類與GSA-LSSVM的汽輪機熱耗率多模型預測[J] .電機與控制學報，2016，20（3）：90.

NIU Peifeng，LIU Chao，LI Guoqiang，et al .Multi-model for turbine heat rate forecasting based on double layer clustering algorithm and GSA-LSSVM [J] .Electric Machines and Control，2016，20（3）：90 .

[19] 李海燕.基于WAMS的電力系統暫態穩定預測方法研究[D].北京：華北電力大學，2006.

[20] 馮康恒，張艷霞，劉志雄，等.基于廣域信息的同調機群在線識別方法[J].電網技術，2014，38（8）：2082.

FENG Kangheng，ZHANG Yanxia，LIU Zhixiong，et al.A wide area information based online recognition of coherent generators in power system[J].Power System Technology，2014，38（8）：2082.

（編輯：邱赫男）