基于神經網絡的正弦波函數擬合實現研究

陳豪 吳健

摘? 要：針對在人工智能教學當中，學生掌握線性回歸之后對其他的初等函數的擬合實現產生的疑問，進行簡單的教學研究。主要采用TensorFlow開源軟件庫，利用Python語言來編寫神經網絡程序。對于已有的呈現正弦波樣態分布的點的集合進行訓練，并通過調整訓練參數最終得到擬合成功的正弦波模型，可以為其他的初等函數的擬合及以后基于訓練模型的預測研究提供一些見解。

關鍵詞：TensorFlow;Python;神經網絡;正弦波;擬合

中圖分類號：TP183;O174? ? ? 文獻標識碼：A 文章編號：2096-4706（2019）21-0004-03

Abstract：We mainly focus on the questions of the fitting of other primary functions after students master linear regression in AI teaching，and then carries out some simple teaching research. It mainly uses TensorFlow open source software library and uses Python language to write neural network program. By training the existing set of points which present the distribution of sinusoidal wave patterns and adjusting the training parameters，the sinusoidal wave model can be successfully fitted，which can provide some insights for the fitting of other elementary functions and the prediction research based on the training model in the future.

Keywords：TensorFlow;Python;neural network;sine wave;fitting

0? 引? 言

在人工智能基礎課程的教學中，對于線性回歸的理解是掌握其他各種復雜的算法規律的第一步，緊接之后要學習的就是根據線性方程進行數據歸類的預測。在各類基礎的人工智能教學材料中，都將線性回歸放在最前面予以講授。在實際的教學過程中，因為學生對于線性方程在中學階段已有掌握，對于線性回歸的知識理解起來也并無大的障礙。但是掌握了線性回歸之后，會自然而然地引向非線性的情況，應該如何進行回歸計算并得出判斷結論。提煉后，得到學生提出的具體問題是：在已知的初等函數中，除了線性方程外，是否其他的函數，如冪函數、對數函數、三角函數等的方程式皆可以成為回歸的判斷結論？本文就這個疑問，從初等函數中選取正弦波函數進行針對性的初步研究。

1? 搭建環境與建立數據集

在人工智能的教學中主要采用主流的TensorFlow開源軟件庫，Google作為其開發者已經推廣多年，各種開發環境與插件較為完善。如果采用國內百度的飛槳（PaddlePaddle）開源庫同樣可以完成此項任務，但主流教學中已經采用了TensorFlow，它的高使用率與高市占率可以讓學生在對口企業中快速上手，有利就業，故采用TensorFlow開發。利用PyCharm IDE，配合安裝Python 3.6版本，并導入TensorFlow的官方包，進行環境運行測試，成功后，指導學生開始開始建立訓練所需的點數據集。這里還需要在PyCharm中安裝pandas和NumPy工具插件，利用它們建立訓練用數據集。

建立數據集分為三步，首先在[-π，π]之間生成400個平均分布的等距離點。關鍵語句為：

train_X = numpy.linspace（-math.pi， -math.pi， 400）

train_X = train_X.reshape（-1， 1）

train_X = train_X.astype（'float32'）

然后，為了讓數據集看起來較為真實，需要添加微小擾動的干擾值，生成干擾值的關鍵語句為：

train_noise = numpy.random.normal（0， 0.03， train_X.shape）

train_noise = train_noise.astype（'float32'）

最后，完成訓練點數據集的生成，關鍵語句為：

train_y = numpy.sin（train_X） + train_noise

這里使用利用Matplotlib庫的pyplot對象顯示訓練集數據的分布狀況，如圖1所示。

2? 建立神經網絡與參數初始化

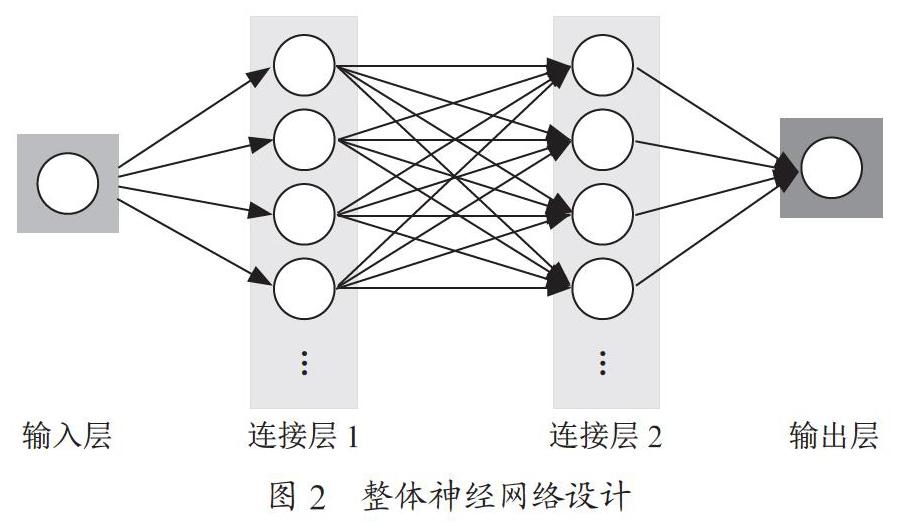
模擬正弦曲線涉及到非線性，這里利用神經網絡來完成。TensorFlow中提供了方便地建立神經網絡的搭建工具。對于正弦波擬合，搭建2層的神經網絡就可以了。這里定義1個前置輸入層、2個連接層、1個輸出層的簡單神經網絡。2個連接層之間的連接的輸出結果需要通過ReLU函數進行激活，然后數據進入第2個連接層，再次使用適當的權重與偏移，直接輸出到輸出層。整體神經網絡的結構如圖2所示。

3? 模型訓練

3.1? 訓練過程

模型的生成需要經過多次重復訓練，最初設置循環2000次，但循環開始后，訓練次數超過1000后圖形基本無變化。經過反復測試得出，設置訓練次數為800次既不耗費過多時間，也可以獲得較好的訓練效果。程序設置每經過40次訓練循環，渲染當前圖形并報告當前的損失函數。渲染當前圖像采用plt的散點圖，y值的顯示范圍設定-1.3到1.3，確保能夠顯示圖形的全部部分，在進入到下一次40倍數的循環次數后，清空當前畫面中已有的渲染點，將新的訓練計算結果與x結對的點實時顯示出來。

for step in range（800）：

session.run（optimizer.minimize（loss））

if step % 40 == 0：

predict = session.run（predict_y）

if step：

ax.lines.remove（lines[0]）

lines = ax.plot（X， predict， 'b-'， lw=5）

plt.title（'step： %d loss： %.4f' %（step， session.run（loss）））

3.2? 結果擬合

經過多次循環運算之后形成了擬合樣態效果。整體圖形的變化趨勢是，開始圖形變換比較快，每經過40次循環后擬合彎曲形態和角度會有很大變化，但到了100次之后，變化幅度變小，圖形只在細微的部分發生變化。觀察損失函數的變化也具有這樣的趨勢。所以不進行平均取樣展示，而是先前的取樣間隔為40次，后期雙倍次數取樣。這里具體取樣的是第0次、第40次、第80次、第120次以及第200次、第280次、第360次、第440次的擬合結果。損失函數也從最初的23.3060急速下降到了后期在0.0100以下，并緩慢變化到0.0040。抽取各次的圖形后漸進的效果如圖3所示。

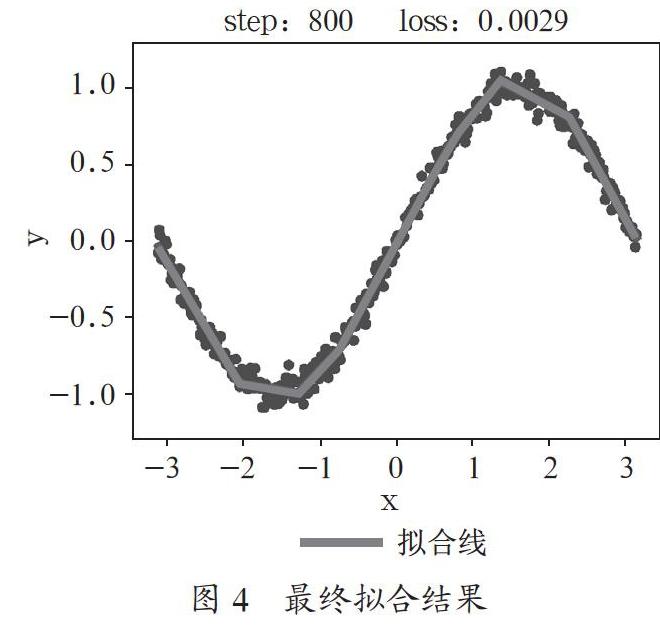
完成800次循環之后，最終擬合的圖像如圖4所示。損失函數降到0.0029。如果繼續增加訓練次數，損失函數無法繼續下降，甚至會重新回到0.0030以上，所以本次訓練的能夠達到的損失函數最低為0.0029。

可以看到，其實在400次循環后，擬合效果已經較好。到800次結束時，紅色擬合線已經基本與正弦曲線重疊，正弦函數模擬模型訓練成功，可用于之后的預測。

4? 結? 論

通過以上的操作，利用神經網絡，通過已有的訓練數據集，實現了正弦波曲線的擬合。解答了學生的提出的疑問。還可以通過修改程序實現其他三角函數的擬態，以及其他初等函數，例如指數函數、對數函數，包括混合初等函數的擬合，學生可以利用之前學習到的高等數學知識進行舉一反三的訓練，增強對高等數學在人工智能中應用的理解。接下來，可以利用TensorFlow的模型保存與重載機制，進行新進數據的狀態預測。總之，利用好TensorFlow或者PaddlePaddle開源工具，配合Python語言，將其融入到人工智能的教學中，以直觀可視的方式讓學生了解艱深的人工智能的知識。

參考文獻：

[1] 劉帥奇，趙杰，劉明，等.新工科背景下基于教師科研成果轉化的實踐教學研究 [J].課程教育研究，2019（14）：39-40.

[2] 楊沛，譚琦，丁月華.一種面向非線性回歸的遷移學習模型 [J].計算機科學，2009，36（8）：212-214+242.

[3] 周飛燕，金林鵬，董軍.卷積神經網絡研究綜述 [J].計算機學報，2017，40（6）：1229-1251.

[4] 徐曉.計算機視覺中物體識別綜述 [J].電腦與信息技術，2013，21（5）：4-6+41.

[5] 盧宏濤，張秦川.深度卷積神經網絡在計算機視覺中的應用研究綜述 [J].數據采集與處理，2016，31（1）：1-17.

作者簡介：陳豪（1982-），男，漢族，江蘇鹽城人，講師，碩士，主要研究方向：人工智能、大數據技術;吳健（1985-），男，漢族，江蘇蘇州人，實驗師，碩士，主要研究方向：軟件技術。