機械能守恒定律的表達形式及其應用
魏天明 鄭口中學 河北省衡水 253800
我們知道,機械能守恒定律是指在只有重力或彈力對物體做功的條件下(或者不受其他外力的作用下),物體的動能和勢能(包括重力勢能和彈性勢能)發生相互轉化,但機械能的總量保持不變。對于機械能守恒的理解,我們要注意如下三種情況:①只受重力作用,如在不考慮空氣阻力的情況下的各種拋體運動,物體的機械能守恒;②受其他力,但其他力不做功,只有重力或系統內的彈力做功;③系統內的彈力做功伴隨著彈性勢能的變化,并且系統內彈力做功等于系統彈性勢能的減少量。
一、準確理解機械能守恒定律
對于機械能是否守恒的判斷方法有三種:①直接判斷:機械能包括動能、重力勢能和彈性勢能,判斷機械能是否守恒可以看物體或系統機械能的總和是否變化;②從做功的角度判斷:若物體或系統只有重力或系統內彈力做功,雖受其他力,但其他力不做功,機械能守恒,諸如繩子突然繃緊,物體間非彈性碰撞等,機械能均不守恒;③從能量轉化的角度來判斷:若物體系統中只有動能和勢能的相互轉化而無機械能與其他形式的能的轉化,則物體系統機械能守恒。
而機械能守恒定律的表達形式有許多,經常涉及的有下列三種形式:
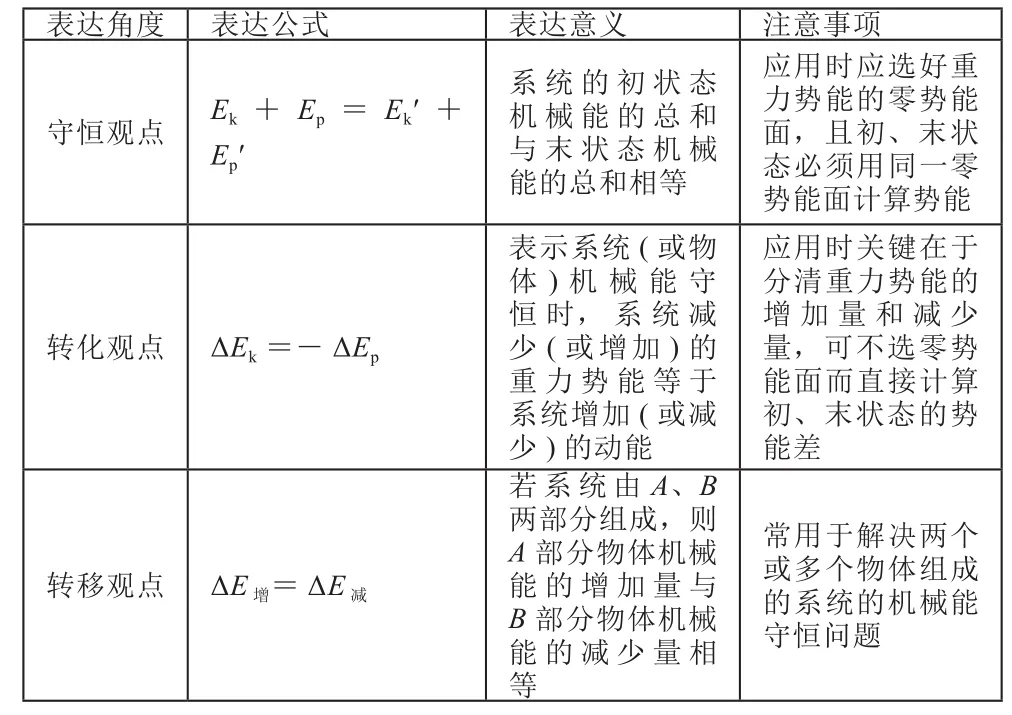
表達角度 表達公式 表達意義 注意事項守恒觀點 Ek+ Ep= Ek′+Ep′系統的初狀態機械能的總和與末狀態機械能的總和相等應用時應選好重力勢能的零勢能面,且初、末狀態必須用同一零勢能面計算勢能轉化觀點 ΔEk=-ΔEp表示系統(或物體)機械能守恒時,系統減少(或增加)的重力勢能等于系統增加(或減少)的動能應用時關鍵在于分清重力勢能的增加量和減少量,可不選零勢能面而直接計算初、末狀態的勢能差轉移觀點 ΔE增=ΔE減常用于解決兩個或多個物體組成的系統的機械能守恒問題若系統由A、B兩部分組成,則A部分物體機械能的增加量與B部分物體機械能的減少量相等
單物體多過程機械能守恒問題:劃分物體運動階段,研究每個階段中的運動性質,判斷機械能是否守恒。
對于多物體組成的系統的機械能守恒,一般選用ΔEp=-ΔEk或者ΔE增=ΔE減形式,優勢在于不用選擇零勢能面。解題時,需要找到兩物體的速度關系確定系統動能的變化,同時找到兩物體上升或下降的高度關系確定系統重力勢能的變化,再按照系統動能的變化等于重力勢能的變化列方程求解。此類問題中,尋找兩物體的速度關系、高度變化情況以及機械能的轉化情況是求解問題的關鍵。
二、利用機械能守恒定律解決物理問題
1、單個物體的機械能守恒
【例1】在一斜面頂端,將甲乙兩個小球分別以v和v/2的速度沿同一方向水平拋出,兩球都落在該斜面上。甲球落至斜面時的速率是乙球落至斜面時速率的 ( )
A. 2倍 B. 4倍 C. 6倍 D. 8倍
【解析】此題將平拋運動、斜面模型、機械能守恒定律有機融合,綜合性強。對于小球在斜面上的平拋運動,一般利用平拋運動規律和幾何關系列方程解答。
設甲球落至斜面時的速率為v1,由平拋運動規律,,設斜面傾角為θ,由幾何關系,得小球拋出到落在斜面上機械能守恒,則,聯立以上各式得同理乙球落至斜面時的速率因此本題正確答案為A。
2、系統的機械能守恒
【例2】如圖所示,釘子A、B相距5l,處于同一高度.細線的一端系有質量為M的小物塊,另一端繞過A固定于B.質量為m的小球固定在細線上C點,B、C間的線長為3l。用手豎直向下拉住小球,使小球和物塊都靜止,此時BC與水平方向的夾角為53°。松手后,小球運動到與A、B相同高度時的速度恰好為零,然后向下運動。忽略一切摩擦,重力加速度為g。求小球向下運動到最低點時,物塊M所受的拉力大小T。
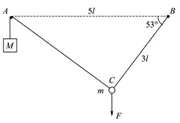
【解析】根據機械能守恒定律,小球向下運動到最低點即為小球的起始點。顯然,此時AC垂直于BC。設此時AC方向的加速度大小為a,重物受到的拉力為T,小球受AC的拉力T′=T
對小物塊M,根據牛頓運動定律,有 Mg–T=Ma
對小球m,根據牛頓運動定律,有 T′–mgcos53°=ma解得
3、多個物體的連接體問題
【例3】質量均為m的小物體A和B分別系在一根不計質量的細繩兩端,繩子跨過固定在傾角θ=30°的斜面頂端的定滑輪上,且斜面固定在水平地面上。開始時把物體B拉到斜面底端,繩與斜面平行,這時物體A離地面的高度為1.8m,如圖所示,若不計一切摩擦,從靜止開始放手讓它們運動,g取10m/s2,求物體A著地時的速度。
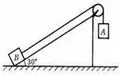
【解析】物體A著地之前,AB組成的系統機械能守恒,設A落地時的速度為v,系統動能的增加量等于系統重力勢能的減少量,則得
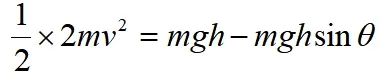
代入數據得:v=3m/s
機械能守恒定律作為物理學的核心知識,是每年高考必須涉及的內容,即可能是選擇題,也可能是計算題,甚至也可能以實驗題的形式出現,對此,我們必須引起足夠的重視。

