小樣本結構參數不確定性量化及傳遞分析的信息擴散方法

駱勇鵬，魯四平，劉景良

（1.福建農林大學 交通與土木工程學院，福州350108；2.中南大學 土木工程學院，長沙410075）

實際工程結構在制造、加工、裝配、建模等環節中不可避免地存在各種不確定性因素，如制造誤差及載荷不確定性等，使得結構性能也表現出一定的變異特性。若在結構分析時忽略這些不確定性因素的影響，采用確定性模型和確定性方法進行分析，可能出現理論分析和實際結構響應不吻合等問題，對結構的安全分析和設計產生不可忽略的影響[1-3]。

當樣本充足時，概率模型是對不確定性進行度量的一種有效辦法[4]。此時，不確定性通過具有某種分布形式的隨機變量或隨機過程來量化，并以此開展結構的不確定性傳遞分析[5]。目前該方面的研究已取得一定的成果。Doebling 等[6]提出了基于蒙特卡羅和有限元分析的不確定性正向傳遞計算方法。徐騰飛等[7]利用蒙特卡羅與鋼筋混凝土非線性有限元法，研究鋼筋混凝土梁在服役期間變形隨機性的變化規律。該分析過程每次加載的非線性分析次數為10 000 次，計算成本較大。為了彌補蒙特卡羅有限元分析方法的不足，宗周紅等[8]提出一種基于響應面模型的蒙特卡羅模擬，并將其應用到下白石大橋的不確定性分析和量化中，在保證模型精度的前提下提高計算效率。

值得注意的是，實際工程中因條件限制往往不能獲取足夠的樣本數據來估計隨機變量的概率密度函數。現有研究成果只能通過假定不確定性參數的概率密度函數，進而開展不確定性傳遞分析。也有學者提出通過擬合優度檢驗（如K-S檢驗）等方法來估計不確定性參數的概率分布[9]。在樣本個數較多的情況下，該方法是可行的。但是當樣本數量較少時，所確定的概率分布本身具有一定的不確定性[10]，甚至可能出現假定的概率密度函數與實際不符的情況，此時將產生較大的誤差，進而影響結構實際服役性能評價。

因此可以說不確定性分析和設計結果的準確性與真實性很大程度上依賴于不確定性源的量化。概率密度函數的選取對不確定性分析結果有較大影響，受工程實際可獲取信息的局限，如何基于有限樣本對不確定性參數進行量化及傳遞分析是當前的發展重點[4]。信息擴散理論通過將單值樣本轉換成概率形式表達的模糊集值樣本，進而對非完備樣本信息進行有效處理[11]，可在一定程度上解決結構不確定分析中概率分布難以確定的問題，目前已逐步應用于測繪工程、災害評估、巖土工程等領域。本文將其引入到不確定性量化和傳遞分析中，提出新的不確定性參數量化和不確定性傳遞分析方法，以數值算例和試驗鋼板模態頻率不確定性分析為例，驗證所提方法的可行性及可靠性。

1 基于信息擴散的不確定性參數量化及傳遞分析

1.1 不確定性參數概率密度函數估計

信息擴散原理的基本思想為：設X是不確定性參數的已知觀測樣本。li為Xi的觀測值。若X是非完備的，則存在擴散函數μ(x)，使得li所獲得的量值為1 的信息可根據μ(x)的量值擴散，且擴散得到的原始信息分布能夠更好地反映總體規律[11]。

根據上述原理對母體的概率密度函數進行估計的過程稱為擴散估計，其定義如下：

設μ(x)為定義在[-∞,+∞] 上的一個Borel可測函數則稱

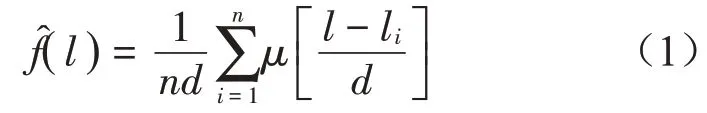
由式（1）可知，要對不確定性參數的概率密度函數進行估計，首先要確定擴散函數μ(x)和窗寬d[11]。黃崇福提出了基于分子擴散理論的正態擴散函數和基于擇近原則的經驗窗寬確定方法[11]。但是該方法不適用于所有分布（如非對稱和非正態分布），且根據不同窗寬計算得到的母體概率密度函數的估計精度是不同的[12]。

為了提高母體概率密度函數的估計精度及擴大其適用范圍，王新洲等提出可在母體概率密度函數估計的均方誤差最小準則求得最優窗寬。而在確定最優窗寬前要先確定最優擴散函數。同樣根據均方誤差最小準則，王新洲等推導出了最優擴散函數的形式[13]。研究表明采用最優窗寬估計母體概率密度函數，其精度比經驗窗寬估計母體概率密度函數要高很多，并且其曲線能很好地逼近理論分布曲線[13]。為此，本文也采用最優窗寬和最優擴散函數來獲得不確定性函數的概率密度函數。

根據文獻[13]中的推導，使母體概率密度函數估計的均方誤差最小的最優擴散函數的形式為

最優窗寬的迭代公式

第三，創新知識體系。要建立獨立學院法學專業新的教材體系，它既不是普通本科教材的濃縮，更不是刪減，而是知識體系的創新。新教材體系要以專業人才培養目標為依據，全面提高人才培養素質和教育教學質量，系統地研究、借鑒傳統法學教材的優點，創立新的體例和新的語言風格，既要照顧到法律基礎理論，又要突出實用性。

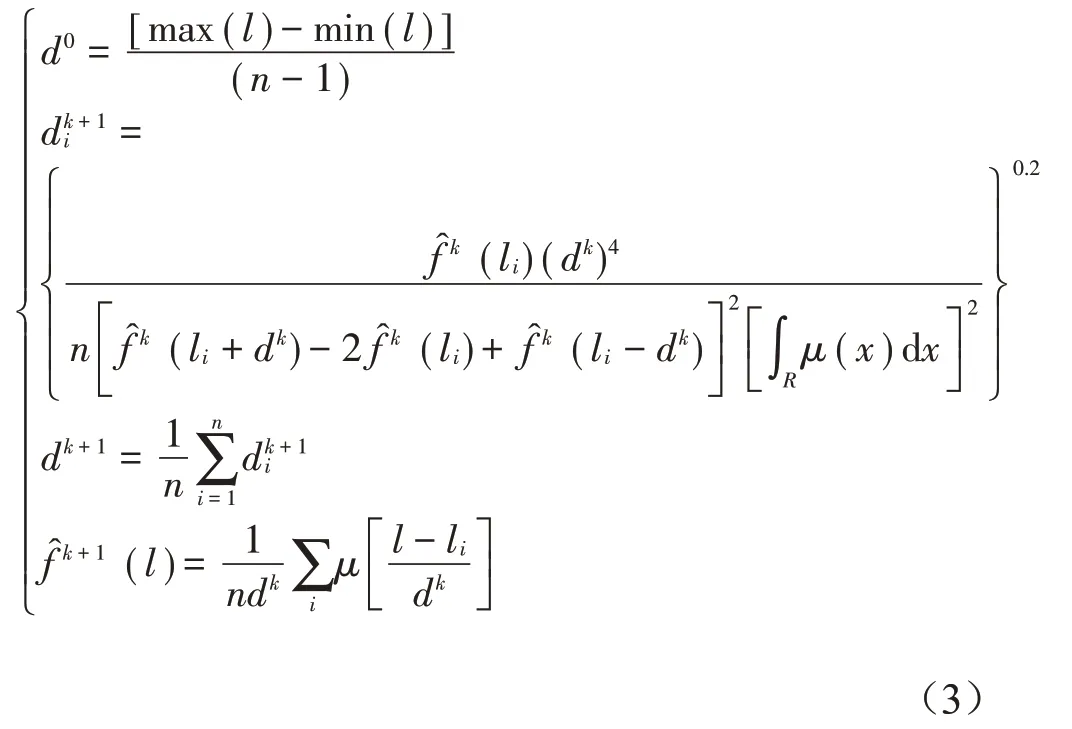
1.2 隨機數生成及參數不確定性量化

考慮到估計的概率密度函數不是常規的概率密度函數，如何生成符合該概率密度函數的隨機數也是一個值得考慮的問題。本文引入接受-拒絕法[14]進行偽隨機數的生成。按照估計的概率密度函數對均勻分布序列的隨機數序列進行舍選。該步驟的具體實現過程[15]為：

首先選擇g(l)作為建議分布的概率密度函數，然后確定一個常數M＞1，使得在l的定義域上均有成立；然后生成服從概率密度函數為g(l)的建議隨機數y和一個服從均勻分布U(0,1)的隨機數u。最后，計算接收準則的概率函數h(l)=，如果u＜h(y)，則接收所生成的隨機數y；反之，則丟棄該隨機數y，重新進行隨機數生成。

通過以上步驟可以生成符合不確定性參數概率密度函數的隨機樣本數據，根據式（4）和式（5）計算不確定性參數的均值和標準差，達到量化結構參數不確定性的目的。

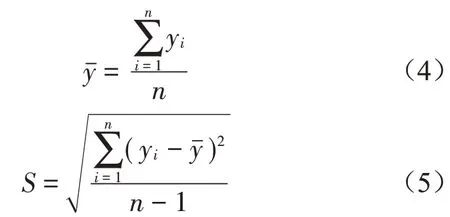
采用接受-拒絕法進行隨機數生成時，首先要選擇常用分布的概率密度函數作為建議概率密度函數，保證g(l)容易被抽樣（本文以均勻分布的概率密度函數作為建議概率密度函數）。其次Mg(l)要能夠完全罩住，且形狀盡量與相似，這樣可以提高抽樣的效率[15]。

1.3 不確定性傳遞分析

為快速計算參數不確定對結構響應的影響，基于逐步回歸分析理論，建立反映參數與響應之間的復雜關系的不完全二次多項式響應面模型[16]，如式（6）所示。

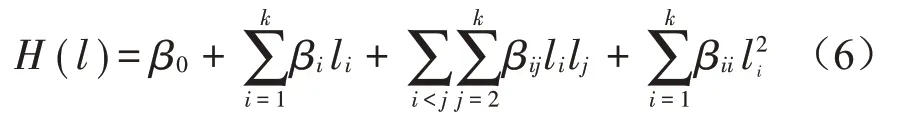
式中：li∈[lli,lui]，lli、lui是參數的取值范圍；β0、βi、βij、βii是回歸系數。

將隨機樣本代入響應面中快速計算隨機樣本對應的結構響應，經統計分析可得響應的均值和標準差，從而估計多個參數變異對結構動力響應變化的影響。

圖1為所提的小樣本結構參數不確定性量化及傳遞分析的信息擴散方法的計算流程。

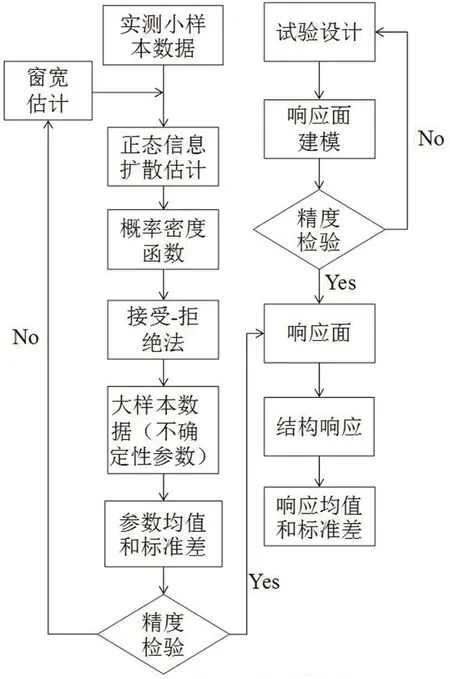
圖1 所提方法計算流程圖

2 數值算例

以4自由度質量-彈簧系統（如圖2所示）來驗證所提方法的有效性。首先假設系統的不確定性均來源于剛度參數的不確定性。其中k1和k2真實值服從均值為1，標準差為0.1的正態分布，其余參數真實值設置為

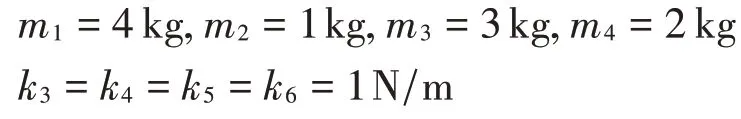
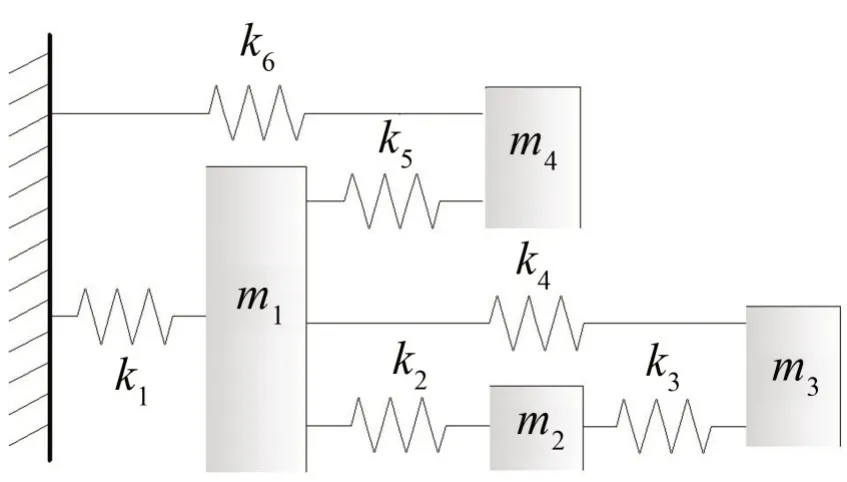
圖2 4自由度質量-彈簧系統

2.1 參數不確定性量化

以k1參數為量化對象，根據k1所服從的概率分布函數，分別隨機抽取200 個數據作為真實不確定性參數的測量數據，其中均值為0.992 9，標準差為0.098 3。分別從200 個數據中抽取前5 個、10 個、15個、20個和25個數據作為小樣本實測數據。基于提出的量化方法對剛度參數k1進行量化，均值和標準差的估計結果如表1所示。

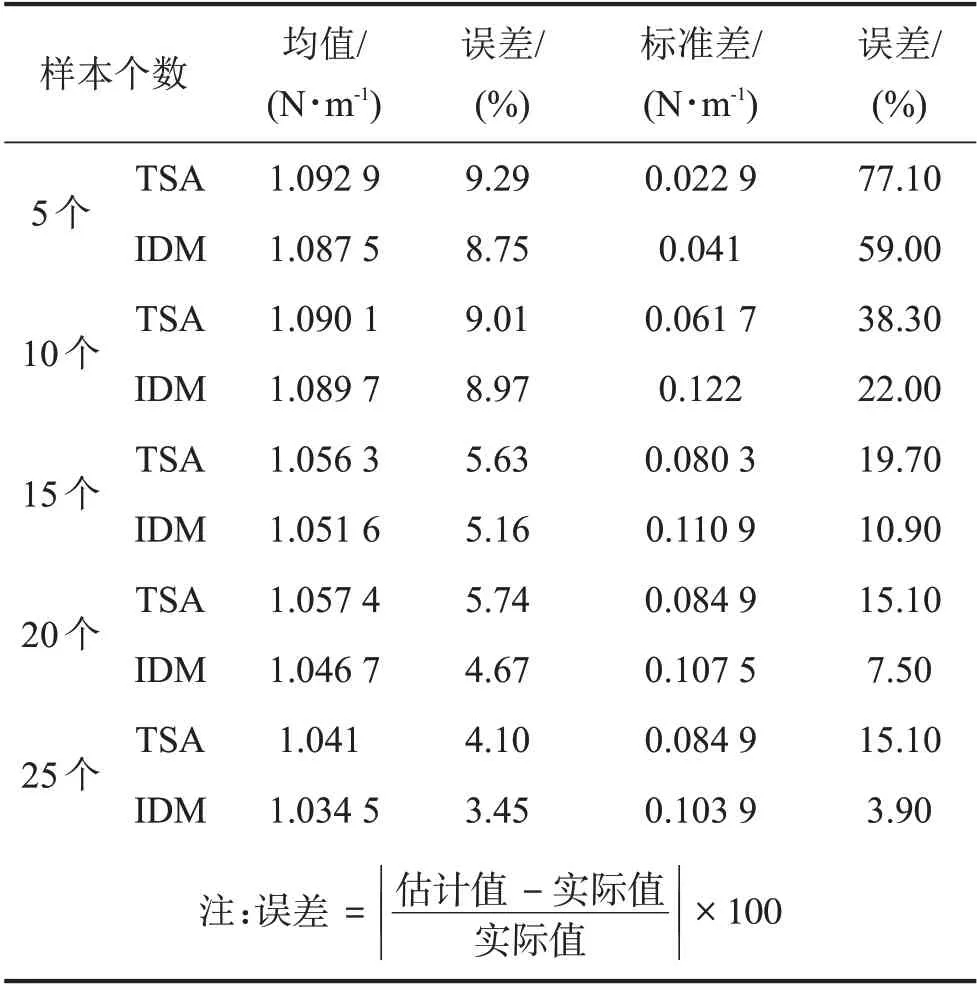
表1 k1參數量化結果分析

表1同時給出直接基于5 個、10 個、15 個、20 個和25 個k1數據計算得到的均值和標準差。為了便于描述，將所提的基于信息擴散的參數不確定性量化方法簡稱為IDM（Information Diffuse Method）；將直接對小樣本數據進行統計分析的方法簡稱為TSA（Traditional Statistical Analysis）。由表1可知，通過IDM 計算得到的均值和標準差相較于TSA 更接近于模擬實測變量的取值情況，尤其是標準差的誤差精度得到顯著提高。如圖3所示。

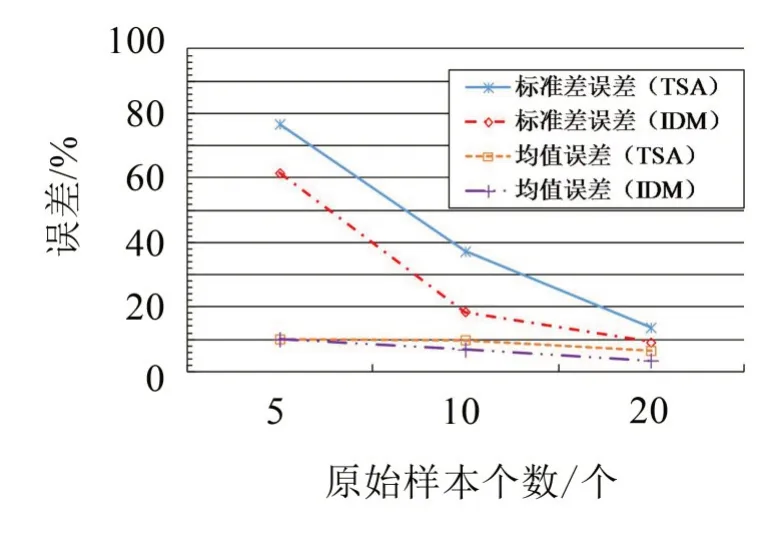
圖3 預測和實際概率統計特征值的誤差

從圖3可知，IDM 和模擬實測值的誤差隨著樣本點個數的增加而減小，當樣本個數為20 個時，均值和標準差的誤差分別為4.67%和7.5%，滿足工程精度要求。參數k2的量化過程及結果與參數k1類似，限于篇幅，不再贅述。

2.2 不確定性傳遞分析

以20 個數據作為小樣本實測數據，分別根據k1和k2的量化結果，計算2 個剛度參數不確定性對質量-彈簧系統的前4 階模態頻率的影響，結果如表2所示。

從表2可知，采用所提的不確定性方法及傳遞分析計算得到的前4階模態頻率均值與模擬實測模態頻率均值吻合良好，最大誤差為2.46%。前4 階模態頻率標準差與模擬實測模態頻率標準差最大誤差為-14.88%。從圖4和圖5可知，預測頻率和模擬實測頻率的分布范圍較為接近，驗證了所提方法的可行性及可靠性。

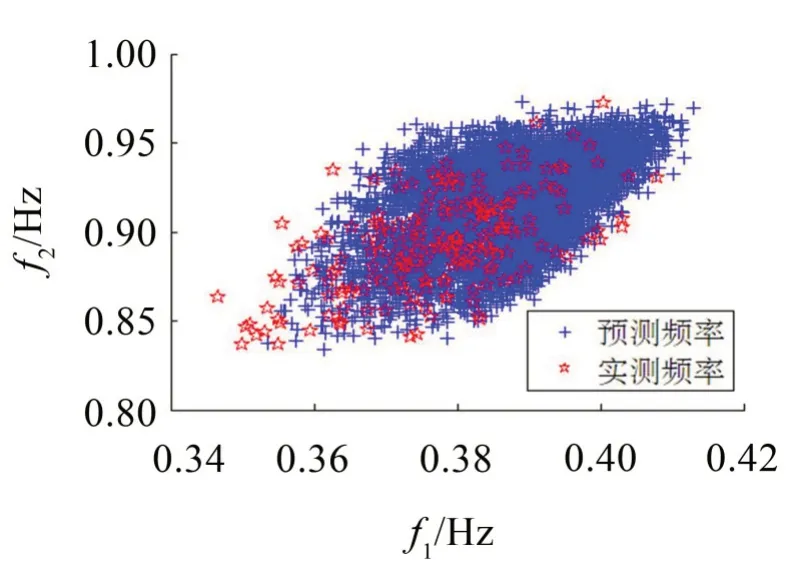
圖4 預測和模擬實測的第1階、2階模態頻率散點圖

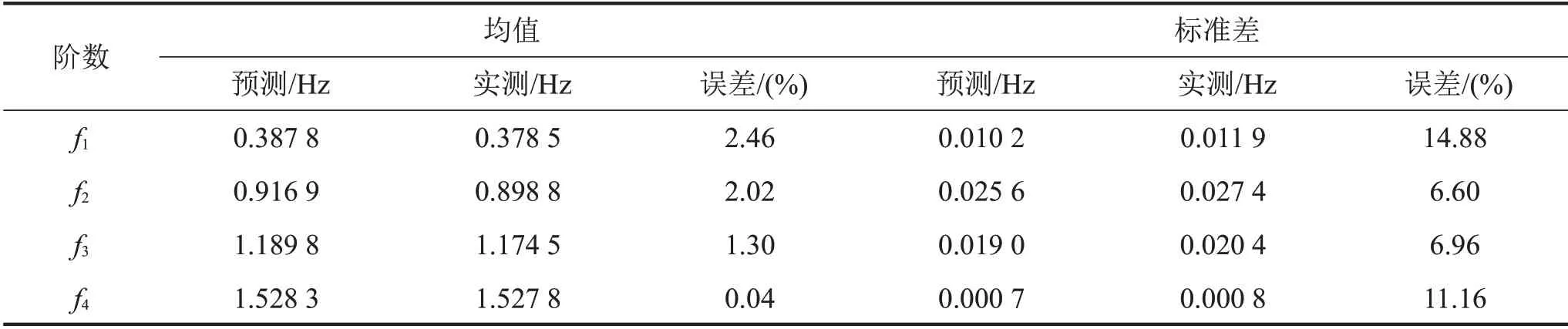
表2 預測頻率與實測模態頻率概率統計特征值

表3 頻率實測值的統計特征值[17]

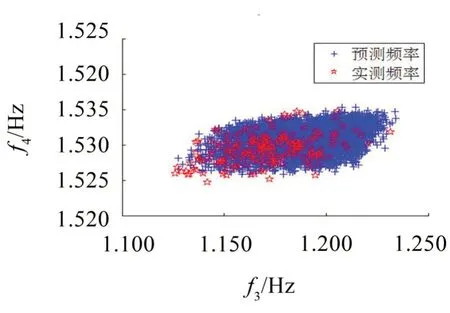
圖5 預測和模擬實測的第3階、4階模態頻率散點圖

3 試驗鋼板頻率響應不確定性分析

以33 塊具有相同名義尺寸及材料參數的鋼板為研究對象[17]，在自由邊界條件下，采用錘擊法對33塊鋼板進行模態試驗，得到33 塊鋼板的前5 階模態頻率值及其統計值，如表3所示。

鋼板模態試驗示意圖如圖6所示。

圖6 鋼板模態試驗示意圖

3.1 材料參數不確定性量化

該組鋼板的名義尺寸為564 mm×110 mm×1.45 mm，彈性模量、剪切模量、質量密度的名義取值分別為210 GPa、83 GPa 及7 860 kg/m3。在不考慮測量誤差影響的前提下，文獻[17]采用隨機模型修正方法對鋼板的彈性模量E和剪切模量G的均值和標準差進行了估計，結果如表4和表5所示。本文根據隨機模型修正預測的材料參數均值和標準差，假定其服從正態分布，分別隨機抽取20個鋼板彈性模量和剪切模量值作為模擬實測值。

基于20個樣本，采用所提方法對鋼板材料參數不確定性進行量化。表4和表5給出了均值和標準差的量化結果。

表4 預測及模擬實測參數均值

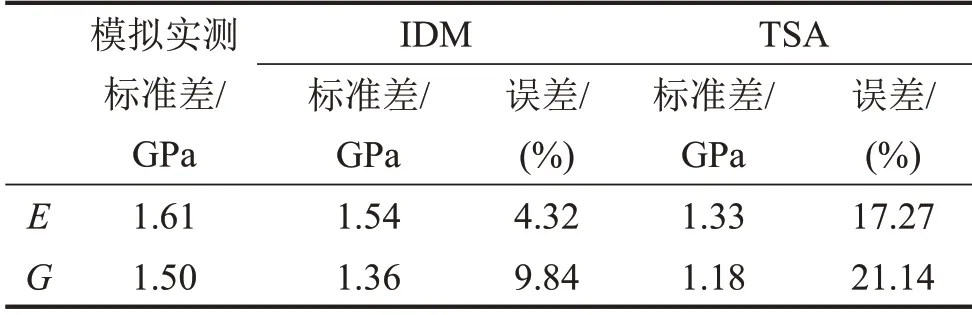
表5 預測及模擬實測參數標準差

從表4和表5可知所提方法估計的均值誤差最大為0.15%，標準差誤差最大為9.84%，相較于TSA的計算結果而言，有較大改善，特別是標準差的估計精度上，有明顯改變，說明所提方法在小樣本的情況下可以有效地估計總體的均值和標準差。

3.2 不確定性傳遞分析

為了快速計算材料參數不確定性引起的鋼板前5階模態頻率的變異程度，采用中心復合設計確定試驗點，結合逐步回歸分析方法，得到前5階模態頻率的響應面模型，其中第1 階模態頻率響應面模型如式（7）所示。

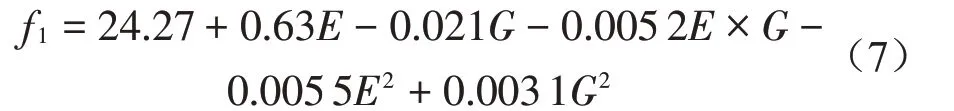
根據不確定性參數量化結果，隨機抽取2 000個樣本點代入各階響應面模型中，快速計算前5 階模態頻率值并進行概率統計分析，結果如表6所示。

從表6可知，前5 階模態頻率均值最大誤差為1.23%，標準差最大誤差為15.88%，滿足工程精度要求。從圖7可知，實測模態頻率大部分在隨機抽樣范圍里面，預測模態頻率和實測模態頻率的分布基本吻合，進一步說明前述材料參數不確定性量化結果的準確性。

4 結語

本文在不確定性分析中引入信息擴散理論，提出基于信息擴散理論的小樣本結構參數不確定性量化及傳遞分析方法。質量-彈簧系統數值模擬算例和鋼板試驗表明不確定性參數估計精度隨著樣本點個數的增加而增加，當樣本個數為20個時可得到較好的估計結果，在一定程度上解決了小樣本參數概率密度函數難以確定而導致參數不確定性量化困難的問題。

表6 頻率實測值及統計值

圖7 預測和實測的第1－3階模態頻率散點圖