球式自動平衡裝置的動力學特性分析

王忠誠，陳海衛，王 志

（1.江南大學 機械工程學院，江蘇 無錫214122；2.江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫214122）

旋轉機械的振動主要是由偏心不平衡引起的。倘若系統有固定的偏心，可利用動平衡或靜平衡的方法達到平衡。然而，在許多情況下，不平衡質量的分布會隨時間的變化而變化，從而很難預測這種不平衡會在何時何地發生。球式自動平衡裝置是自動定心型的平衡裝置[1]，不需要外部提供任何能量，只利用系統響應所形成的能量來驅動滾球的移動和分布，從而自動地消除轉子的不平衡[2-3]。Rajalingham，Bhat和Rakheja[4]研究了球式自動平衡裝置無衰減動力學系統的穩定性，并利用線性化后的運動方程來確定系統穩定轉速的范圍，從而得出，在達到系統的臨界轉速時轉子的振動減小。Chung和Ro[5]采用極坐標的方式并利用拉格朗日方程推導出了球式自動平衡裝置自治系統的運動方程，并對球式自動平衡裝置的穩定性和動力學特性進行了分析。譚青[6]建立了單自由度振動系統球式自動平衡裝置實驗臺，并通過仿真與實驗驗證了球式自動平衡裝置的減振性能。

本文構建了雙自由度球式自動平衡裝置的平面模型，并對自治系統進行穩定性分析，指出系統達到穩態轉速的條件。

1 球式自動平衡裝置的振動模型

本文的研究對象是一個平面放置的偏心旋轉盤和一個由兩個平衡球組成的自動平衡裝置模型，如圖1所示，包括圓盤，平衡球和懸掛系統。圓盤以恒定的角速度旋轉。點W表示圓盤的質量中心（不包括平衡球）且與旋轉中心C不重合，偏心距為ε。平衡球在固定的軌道中周向運動，軌道半徑為R。

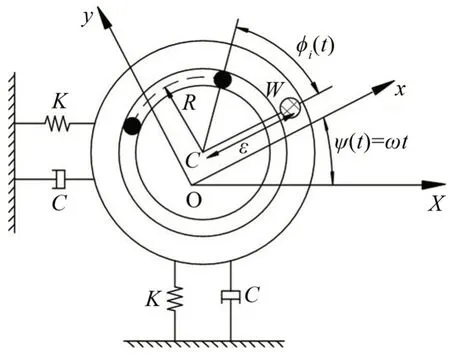
圖1 球式自動平衡裝置模型

本文所采用的符號(單位均采用國際標準單位)：O、C——圓盤中心靜止時和運動時的位置

X、Y——C點在水平和豎直方向的坐標

C、K——圓盤在水平和豎直方向的阻尼系數和剛度

M、m——偏心圓盤與平衡球的質量

R——平衡球周向運動的軌道半徑

ε——偏心距

ψ、φi——圓盤轉角、第i個滾球的轉角

D——球的粘性阻尼系數

M0——系統總質量(M0=M+2m)

圓盤在XY平面中運動，系統的廣義坐標為：

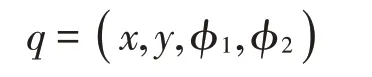
利用拉格朗日方程推導得到系統的運動微分方程

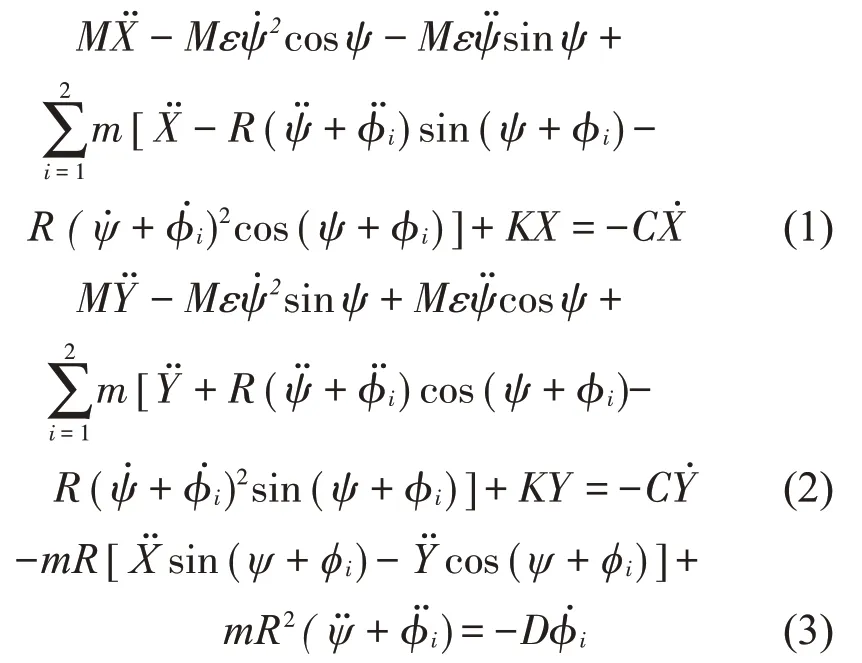
為了簡化計算，上式(1)、式(2)、式(3)中的X、Y、t可通過下面的公式轉化為無量綱形式的X0、Y0、t0，

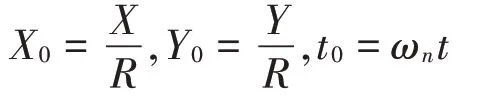
定義如下的無量綱參數

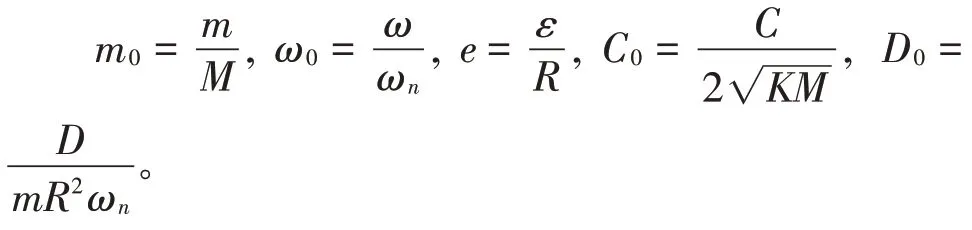
ωn是系統的固有頻率

系統的微分方程可以轉化為如下的無量綱形式

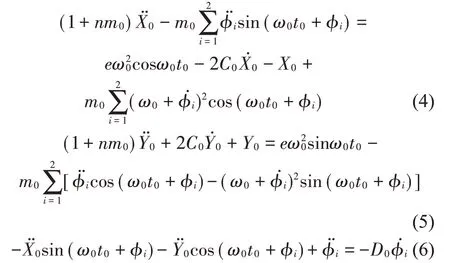
上述得到的模型為非自治系統，其穩態解為周期解。因為周期解的討論較為困難,所以這里進行自治系統的轉化，進而討論其平衡點的穩定性。采用下述旋轉坐標變換[7]的方法將上述系統轉換為自治形式

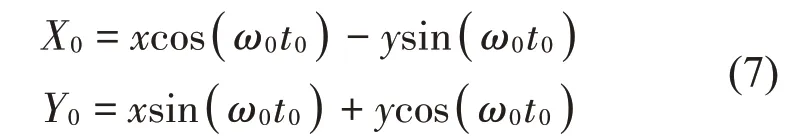
將旋轉坐標帶入式(4)、(5)、(6)，得到系統的自治形式

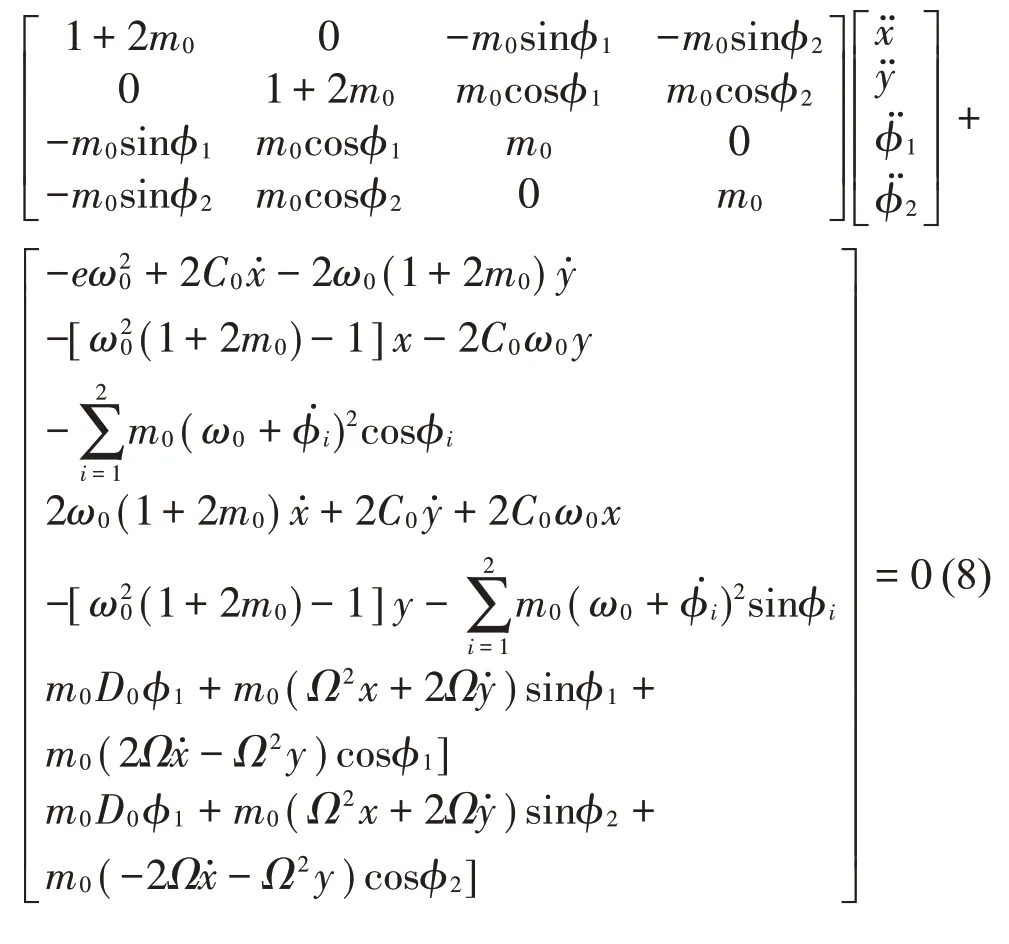
2 自治系統分岔與穩定性分析

本節中對式(8)得到的系統進行穩定性進行分析。首先，通過計算求得系統在不同條件下的穩態解；然后利用AUTO軟件[8]對各個解進行穩定性分岔分析。

2.1 穩態解

系統具有穩態解時，所有關于時間的導數均為零。當系統的質心處在原點時，系統會有一個平衡的穩態解，再根據公式(8)可得

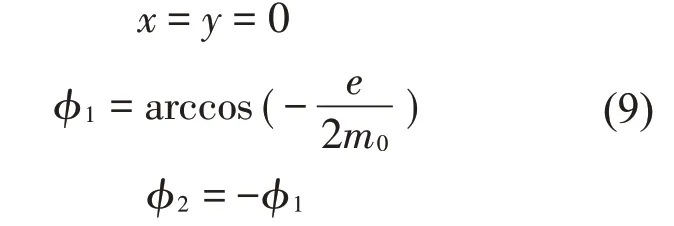
在下面的分析計算中，將公式(9)記為解1。

當系統的質心不在原點，即x,y≠0時，系統會有不平衡的穩態解。根據公式(8)可得

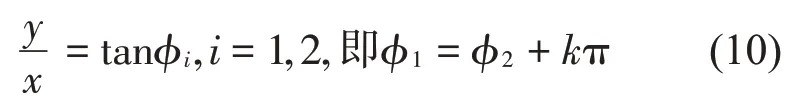
在k=0時對應系統的第一個不平衡的穩態解，也就是說兩個平衡球是重合的狀態（不考慮球的碰撞和球之間的相互作用）。將k=0 及式(10)代入式(8)，從而可以得到

在下面的計算分析中，將式(11)記為解2±。

在k=1時是系統的第二個不平衡的穩態解，此時，2 個平衡球處于相對的位置，與旋轉中心C在一條直線上。將k=1及式(10)代入式(8)，可以得到

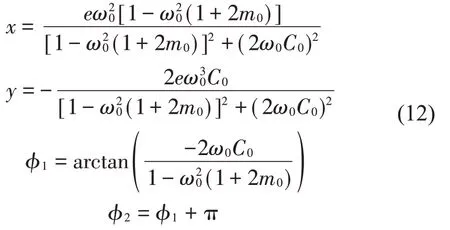
在下面的計算分析中，將公式(12)記為解3。

(a)為解1，兩個平衡球關于偏心對稱；

(b)為解2±，兩個平衡球重合；

(c) 為解3，兩個平衡球與旋轉中心在同一直線上。

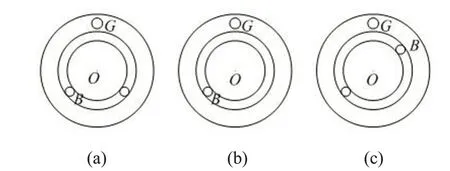
圖2 三個解的示意圖，G代表偏心，B代表平衡球

2.2 數值分岔結果

利用數值分岔軟件AUTO 對式(8)得到的自治系統進行穩定性分析。AUTO是在Linux/Unix系統下運行的軟件，本文使用的版本為AUTO07p。當發生鞍-結分岔時，系統在平衡點處具有一個0特征值。當發生霍夫分岔時，平衡點處系統存在一對共軛復根。該復根穿越了復平面中的虛軸，系統的平衡點也由此變得不穩定。計算過程中各參數的默認值及變化范圍見表1

表1 計算參數

進而可以得到無量綱參數默認值以及變化范圍如表2

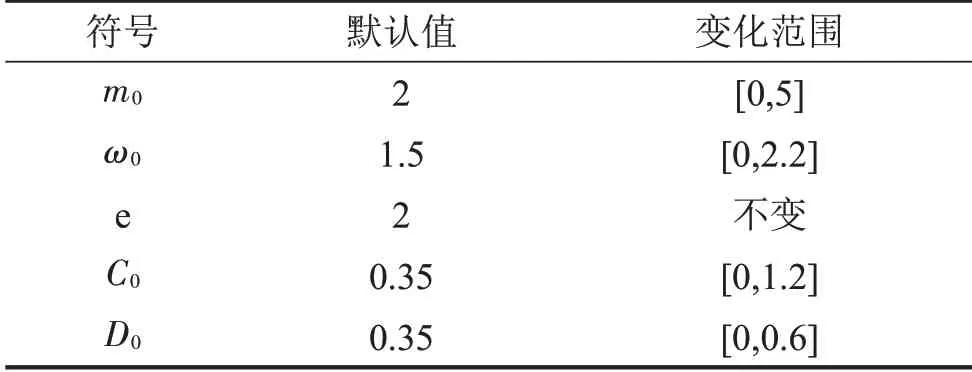
表2 無量綱參數

上述所得的穩態解的存在需具備一定的條件。對于解1，其存在的條件為

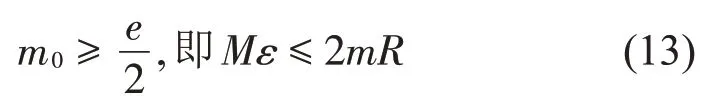
也就是說，為了達到平衡狀態，平衡球的總質量與軌道半徑的乘積要大于偏心質量與偏心距的乘積。當公式(13)兩邊相等時，φ1=π,φ2=-π。說明此時兩個平衡球相對于偏心都處于相對狀態，即兩平衡球重合，恰好對應解2±。在Mε＞2mR時，解1不存在，即在兩個平衡球重合后，平衡的穩態解1開始不存在，這是典型的叉形分岔。

圖3是m0的單參數分岔圖，在圖中，縱坐標為AUTO 默認的L2范數實線為穩定解，虛線為不穩定解，叉形分岔點用△標記，霍夫分岔點用*標記。從圖3可看出,隨著m0的增大,系統中出現了霍夫分岔現象。經過霍夫分岔點后,自治系統的解也從不穩定轉為穩定。平衡解1來自平衡解2±其中之一的叉形分岔PF。

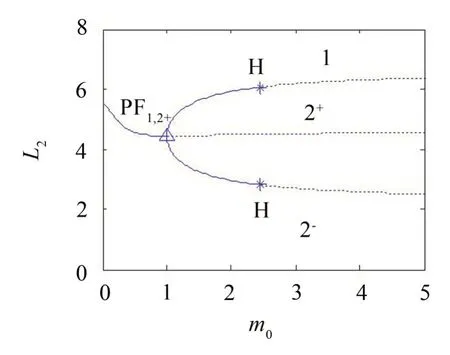
圖3 m0單參數分岔分析，PF代表叉形分岔點，H代表霍夫分岔點

對于兩平衡球處于重合狀態的解2±來說，利用反余弦函數定義域絕對值小于等于1 的性質，聯合式(11)可以得到

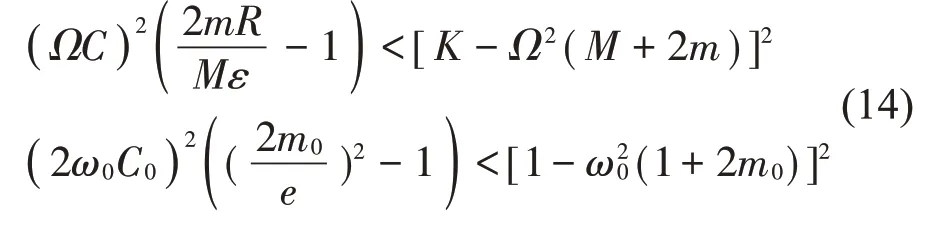
圖4(a)和圖4(b)給出了針對無量綱參數ω0與m0的雙參數分岔結果。在圖4(a)和圖4(b)中，實線對應的是鞍結分岔PF 或者叉形分岔SN，虛線對應的是霍夫分岔H；區域一對應的是平衡解1，區域二對應的是解2±，其余區域沒有對應的穩態解。

鞍結分岔、叉形分岔和霍夫分岔曲線交于一點，即為上文提到的叉形分岔點，該點的坐標為

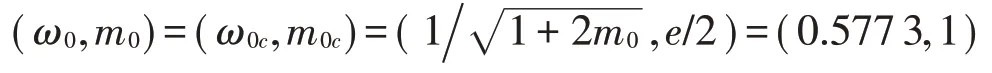
該點坐標轉化為有量綱的形式為

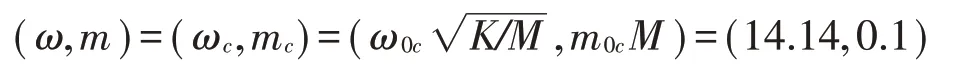
在圖4(a)中，字母的下標對應的解的序號；在圖4(b)中，下標代表該區域是否處于穩定狀態(s代表穩定，u 代表不穩定)。從圖4(a)和圖4(b)中可以得到，對于解1來說，只有當m0＞1時存在，且只在區域二中是穩定狀態；對于解2+來說，在m0＜1 時，解2+一直是穩定的解，而在m0＞1 時，只有當ω0比較小時，即在鞍結分岔曲線SN2±的左側，系統才會處于穩定狀態；對于解2-來說，系統一直處于不穩定狀態。

圖5進一步給出了其他相關物理參數的雙參數分岔分析，圖5(a)、圖5(b)分別表示隨著ω0的增加，穩定邊界與球阻尼D、系統阻尼C的無量綱參數D0、C0的關系。區域一對應的是平衡解1，區域二對應的是解2±，其余區域沒有對應的穩態解。在這2種情況中，在經過鞍節分岔點SN 時解2±開始變得不穩定，而在經過霍夫分岔點H時平衡解1開始變得穩定。

對于解3，無論各參數怎樣取值，式(12)總有意義，即解3一直存在（注意：和解1一樣，通過交換φ1和φ2可以得到兩種形式的解，因為兩個平衡球是完全一樣的，所以兩種形式的解是等價的）。

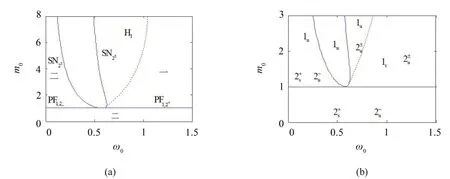
圖4 ω0 -m0雙參數分岔分析

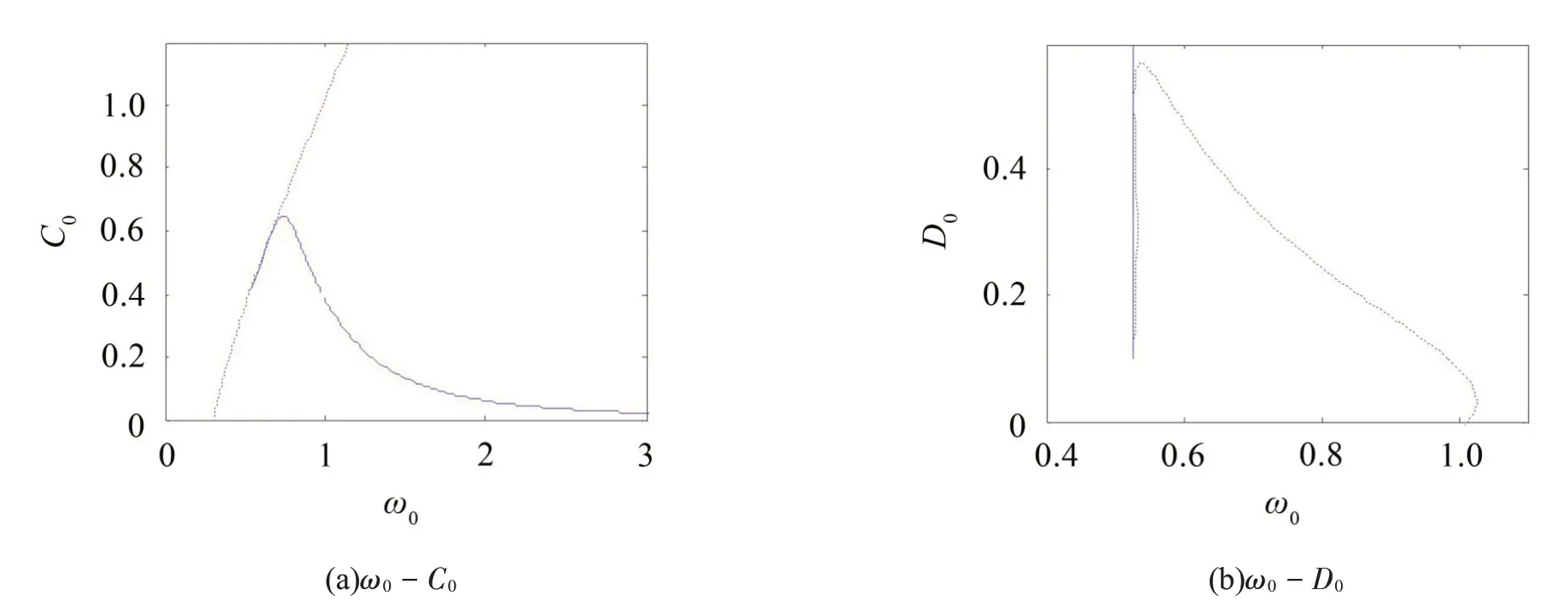
圖5 雙參數分岔分析

3 分岔結果的仿真驗證

在本節中，應用MATLAB軟件進行數值仿真并驗證上一節的分岔結果。各項參數采用表2中的默認值，其他參數的初值設定為

圖4得到了系統不同解的區域以及穩定、不穩定區域，圖6給出了分岔圖中不同區域的數值仿真結果，即徑向振動隨時間的變化。

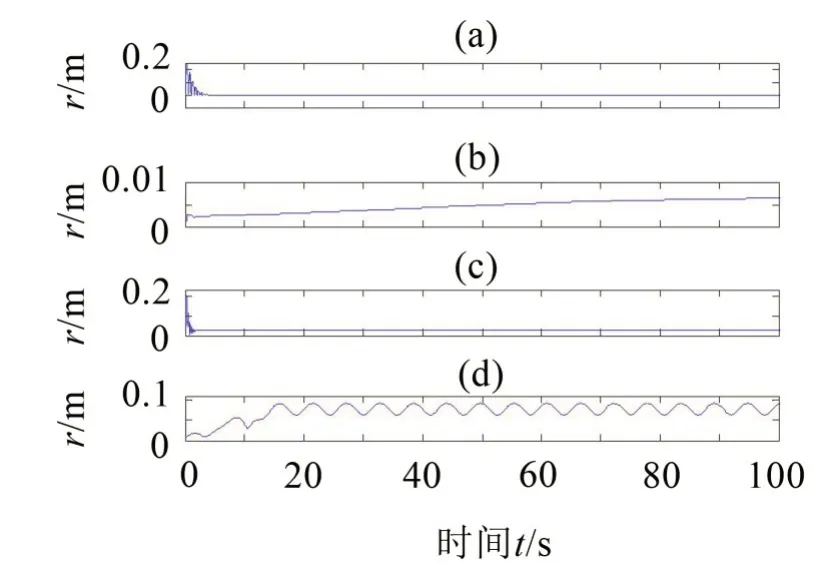
圖6 數值仿真圖

圖6(a)給出了高轉速(ω0=20)以及m0=2 時的仿真結果，該情況對應圖4(a)中平衡解1的霍夫分岔邊界H1的右側，且最終實現了完全平衡的效果。圖6(b)給出了低轉速ω0=0.3 以及m0=2 時的仿真結果，長時間的數值仿真系統都未能達到平衡的效果。圖6(c)給出了平衡球與偏心質量比值較小(m0=0.5)以及ω0=4的仿真結果，對于給定的偏心率e=2，此時并不滿足平衡條件(13)，如同分岔分析所預測的一樣，解2+是穩定的，系統的徑向振動最終穩定在0.025 77。圖6(d)給出的是m0=4、ω0=0.6的仿真結果，圖6(d)可以得知，此時系統沒有穩定的平衡，在該條件下系統具有振蕩的徑向振動。

4 結 語

本文建立了雙自由度振動系統的球式自動平衡裝置的模型，并對其進行了非線性分岔分析，給出系統的雙參數分岔分析圖，從而得到系統的穩定區與不穩定區。最后在MATLAB 中進行數值仿真驗證分岔結果，得到不同參數值情況下的平衡結果。從中可以得到以下結論：

(1)從圖3和圖4可以得到，若每個平衡球的質量與偏心質量之比m0大于偏心率e的一半，且隨著轉速的增加，系統在經過霍夫分岔后即可實現平衡；

(2)在每個平衡球的質量與偏心質量之比m0小于偏心率e的一半時，此時兩平衡球重合，最終系統的振幅會穩定在某個特定的值，從而實現動態平衡。