卡爾曼濾波器在移動機器人定位中的應用

(華北科技學院電子信息工程學院 河北 廊坊 065201)

引言

1960年,卡爾曼發表了用遞歸方法解決離散數據線性濾波問題的論文(A New Approach to Linear Filtering and Prediction Problems)[1]。卡爾曼濾波應用廣泛且功能強大,它可以估計信號的過去和當前狀態,甚至能估計將來的狀態,即使并不知道模型的確切性質[1]。

卡爾曼濾波器又稱為最佳線性濾波器[2]，它的好處有很多，比如：簡單易實現、又是一個純時域的濾波器，不需要進行頻域變換。卡爾曼濾波(Kalman filtering)一種利用線性系統狀態方程，通過系統輸入輸出觀測數據，對系統狀態進行最優估計的算法[3]。由于觀測數據中包括系統中的噪聲和干擾的影響，所以最優估計也可看作是濾波過程。

一、卡爾曼濾波的原理

(一)預測

假設移動機器人正在運動，用它的位置和速度來表示它當前的狀態，t時刻的位置為pt，速度為vt，加速度為ut，那么在t時刻移動機器人的狀態向量可以用一個二維的列向量xt=[pt,vt]T表示。假設移動機器人的加速度量由外部控制量(油門加速或控制命令)得到[4]，如果已知上一時刻的狀態xt-1可推出其在t時刻的速度與位置如下:

移動機器人的速度：vt=vt-1+ut×Δt

其中Δt是兩個時刻的時間間隔，觀察上公式可知輸出變量都只是輸入變量的線性組合，這就是卡爾曼濾波器是最佳的線性濾波器原因，因為它只能描述狀態與狀態之間的線性關系，既然是線性關系，則可改寫成矩陣的形式如下：

vt=0×pt-1+1×vt-1+ut×Δt

把兩個狀態變換矩陣提取出來，公式可以簡化成如下：

由狀態轉移矩陣Ft和控制矩陣Bt表示的移動機器人的狀態轉移公式為：

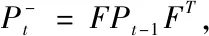
(二)更新

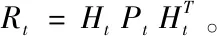
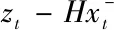
卡爾曼系數Kt作用主要有兩方面，一是權衡預測狀態協方差P和觀測的協方差矩陣R的大小來決定預測模型更可靠，還是相信觀察模型更可靠，若預測模型更可靠，則殘殺的權重就會小一點，若觀察模型更可靠，則殘差的權重就會大一點。第二個作用是把殘差的表現形式從觀察域轉換到狀態域[8]。

最后一步是更新最佳估計值的噪聲分布，即噪聲協方差矩陣的更新，用公式表示為：

二、卡爾曼濾波器的系統模型

綜上所述，我們已經得到了卡爾曼濾波器中的五個公式，在這五個公式中前兩個公式是通過上一時刻的狀態來預測當前時刻的狀態，這表示這并不是最佳的估計值。再把當前時刻的觀測值考慮進去即為更新，經過更新后的值就是最佳的觀測值。

預測：

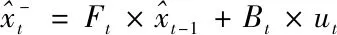
更新：

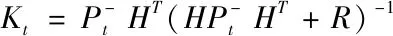
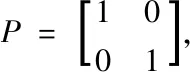
三、結束語

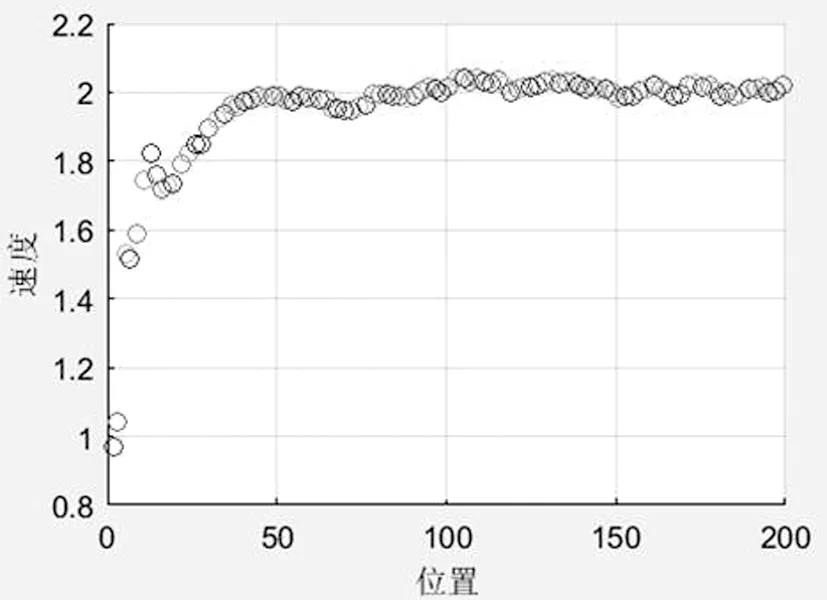
由于卡爾曼濾波在機器人SLAM中主要用于位置估計，所謂的估計值是估計位置坐標，輸入傳感器數據包括碼盤估計的位置，陀螺儀的角速度等。采用卡爾曼濾波的方法來實現移動機器人位置的估計，利用卡爾曼濾波的良好的跟蹤性能，它可以根據當前的觀測量和之前的觀測數據，根據線下那個最小方差原理，求出最優估計。采用遞歸方法解決線性濾波問題，只需要當前的測量值和前一個采樣周期的估計值就能夠進行狀態估計，不需要大量的存儲空間，每一步的計算量小，計算步驟清晰，非常適合計算機處理。最終輸出的最佳估計值用作機器人的當前位置，其由除導航算法之外的其他程序調用。