最大熵原理在推導分子數分布中的應用

慶秉承 劉 萍 陳曉珂 胡 祎 王致遠 胡云婷 韓英卓 田篷勃 方愛平

(西安交通大學理學院，陜西 西安 710049)

在物理學中熵是反映系統無規程度的量度。1948年，Shannon提出信息熵的概念[1]。事實證明，信息熵和熱力學熵有一定的統一性。根據熵增加原理，在一定條件下，孤立系統在達到穩態時，其熵值將會趨于某個極大值。因而在1957年，E.T.Jaynes提出最大熵原理[2]，即：一個穩定宏觀系統某個物理量的信息熵在約束條件下趨于最大值。由于信息熵的大小和該物理量的概率密度分布函數f(x)有如下關系：

式中，f(x)為該物理量的概率密度分布函數；D為概率密度分布函數的定義域。

根據最大熵原理，只需求得使信息熵在約束條件下達到最大值的函數f(x)，便可確定該物理量的概率密度分布函數。為求得f(x)，可以利用拉格朗日法求泛函的約束極值。

最大熵原理被學者廣泛研究，利用最大熵原理，藍風華推導出了麥克斯韋速率分布[3]；晉宏營推導出了電介質極化規律[4]；方愛平、田蓬勃等人應用最大熵原理，在信息缺失的條件下最大效率地實現對全局進行判斷和決策[5]。但鮮有學者用最大熵原理研究分子數密度按自由程以及按高度的分布，本文將利用最大熵原理，研究這些問題。

1 推導分子數密度按自由程分布

在秦允豪先生的熱學教材中，為推導分子數按自由程分布，通過小孔泄流模型，得到了結果[6]。本文通過最大熵原理，重新推導分子數按自由程分布。

利用拉格朗日乘數法，得到

結合約束條件，解得

則最終得到分子按自由程分布服從指數分布，與教材上的結果一致，即為

2 推導分子數密度按高度的分布

在秦允豪先生的熱學教材中，給出了等溫條件下，分子數按高度的分布[6]。而本文將利用最大熵原理，推導考慮溫度分布情況的分子數按高度分布。

2.1 理論推導

設分子數按高度分布的概率密度分布函數為f(h)，考慮分子平均能量應為一個定值，即

式中，m為單個分子平均質量；h為位勢高度(Geopotential height)；k為玻爾茲曼常數；T為熱力學溫標。式中近似認為分子能量僅僅包括重力勢能和分子動能，且空氣分子為剛性雙原子分子。

則根據最大熵原理，有

利用拉格朗日乘數法，得到

得到

將其代入歸一化條件，得到

最后得到(參數β待定)

2.2 結果驗證

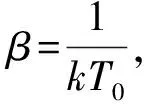
(2) 變溫情況 此時，為了獲得大氣溫度隨高度的變化，參考美國NASA公布的Standard Atmosphere中給出的大氣溫度隨高度變化的數據[7]，數據如圖1所示。

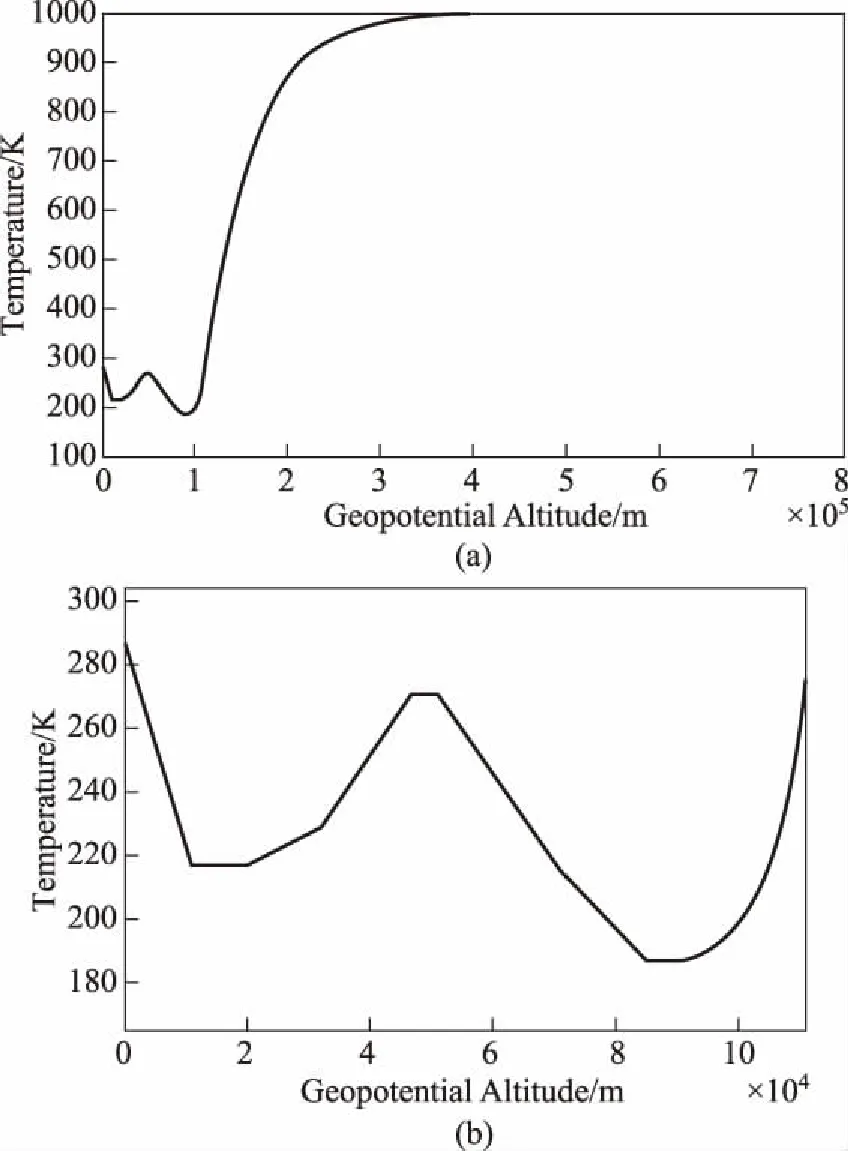
圖1 大氣溫度隨高度變化((a) 為全高度; (b) 為近地區細節)

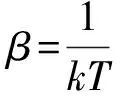
滿足歸一化條件，又由于拉格朗日乘子的唯一性，故該拉格朗日乘子取值是正確的。

由此可以得到分子數按高度分布的情況，由于

則分子數密度n滿足

可見n與f(h)呈正比例關系，將NASA發布的分子數密度隨高度變化的曲線[7]與通過上式計算得到的分子數密度隨高度分布的曲線進行對比，結果如圖2所示。

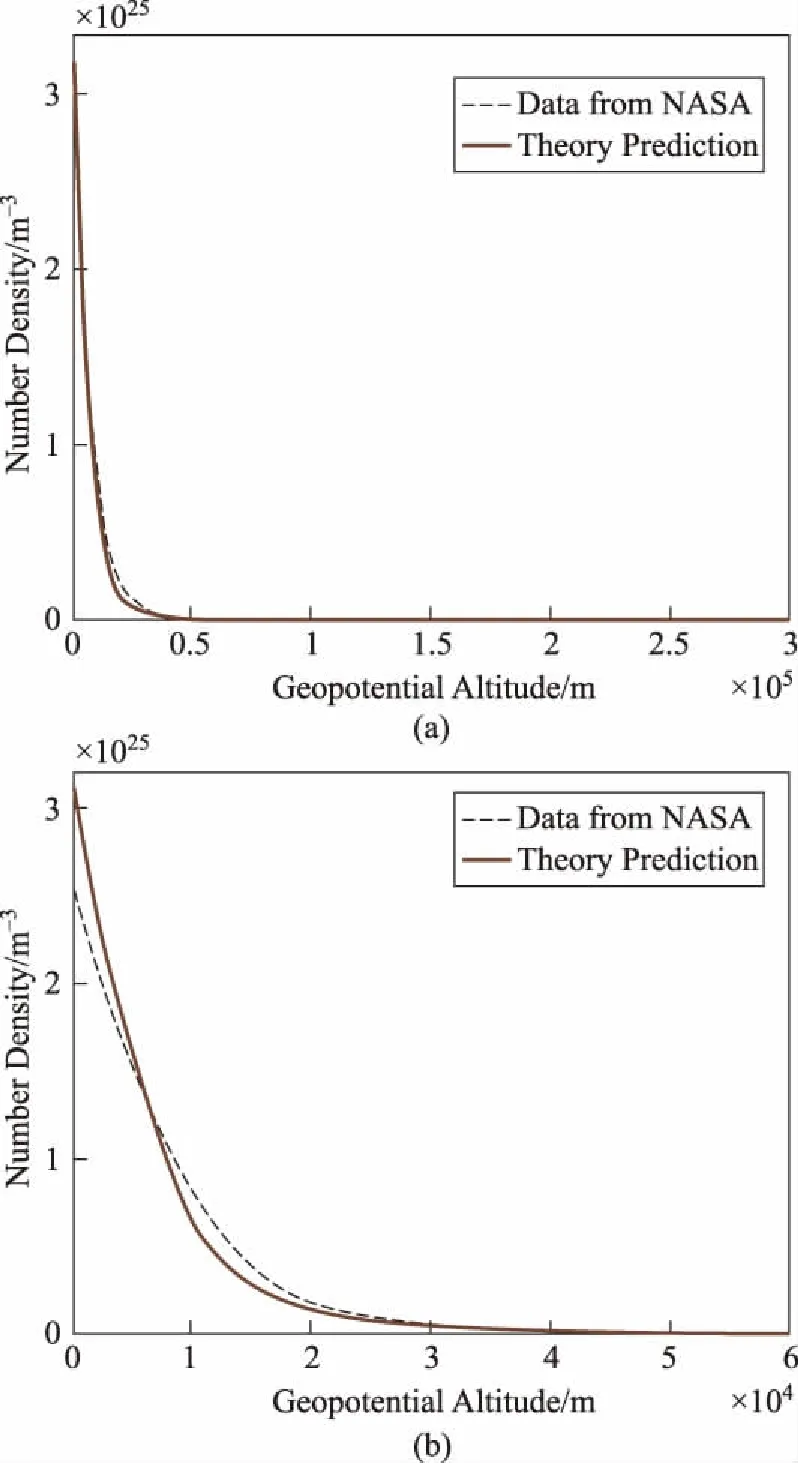
圖2 分子數密度隨高度變化((a) 為全高度; (b) 為近地區細節)

可見二者吻合較好，說明上文通過最大熵原理進行的推導是合理的。

3 結語

本文首次通過最大熵原理研究分子數按自由程的分布，基于更弱的假設，得到的分布函數和教材吻合，有更好的普適性。首次利用最大熵原理研究了溫度變化情況下，分子數按高度的分布，結果和NASA的數據相吻合，該結果將有利于預測更高海拔的分子數分布。上述結果表明最大熵原理在統計物理中的應用是合理的，這或許隱含了統計物理和信息論的內在聯系。