導體球殼內的電場
廖其力 鄧 婭 余 艷
(重慶郵電大學移通學院,重慶 401520)

圖1 點電荷與導體球殼(a) 球殼內點電荷與像點電荷; (b) 球殼內壁上感應電荷隨極角的分布; (c) d=0.05m時的等勢線; (d) d=0.09m時的等勢線
電磁學理論[1,3]中靜電場的基本規律是泊松(Poisson)方程(2φ=-ρ/ε)和拉普拉斯(Laplace)方程(2φ=0),通過求解該方程和邊界條件來研究點電荷與特殊形狀的導體(比如無限大導體平面或者導體球) 相互作用下的電場,也可用格林(Green) 函數來研究點電荷作用下特殊形狀導體周圍空間的電場,但這些方法相對來說較為繁瑣,尤其是求解連續帶電體下特殊形狀的導體周圍空間的電場,其運算量太大無法給出解析結果。但用電動力學中[3]的鏡像法來研究點電荷與無限大導體平面周圍的電場、點電荷與導體球外周圍的電場及作用力,就容易很多。文獻[4~7]將鏡像法應用于研究在連續帶電體作用下導體球(或無限大導體平面)周圍空間的電場,運用疊加原理和Mathematica軟件研究了均勻帶電線狀體與無限大導體平面的電場力及其周圍空間的電場、均勻帶電線狀體與導體球的相互作用力及其導體球外的電勢以及帶電圓環與無限大導體平面和導體球的電磁學問題。鏡像法的原理是:導體球(或無限大導體平面)外的點電荷在導體球(或無限大導體平面)表面上產生的異種感應電荷在導體球(或無限大導體平面)外產生的電場,根據光學成像原理,等效于該點電荷經導體球面(或無限大導體平面鏡)成像于像點處的異種電荷在導體球(或無限大導體平面)外產生的電場。本文從鏡像法得到啟示:根據光學的可逆性原理可知鏡像法具有可逆性,即導體球殼內的點電荷在球殼內壁上產生的異種感應電荷在導體球殼內產生的電場,也等效于該點電荷經球面成像于像點處的異種電荷在導體球殼內產生的電場。運用逆鏡像法和靜電平衡條件,用Mathematica軟件,計算了在導體球殼內任一位置處的點電荷作用下,球殼內壁上感應電荷的分布和殼內空間的電場分布,進一步計算了點電荷和球殼內壁上感應電荷的相互作用的電場力。并繪出在球殼內任一位置處的點電荷作用下,殼內壁上感應電荷隨位置和角度的分布圖像、導體球殼內空間的電勢隨位置的分布,以及點電荷與球殼內壁上感應電荷的電場力隨位置的變化。再運用“逆鏡像法”計算了球殼內沿徑向放置的均勻帶電線狀體作用下,球殼內壁上感應電荷的分布規律和球殼內的電場,以及它們之間的相互作用力,也給出了相應變化的圖像。
1 點電荷作用下導體球殼內的電場
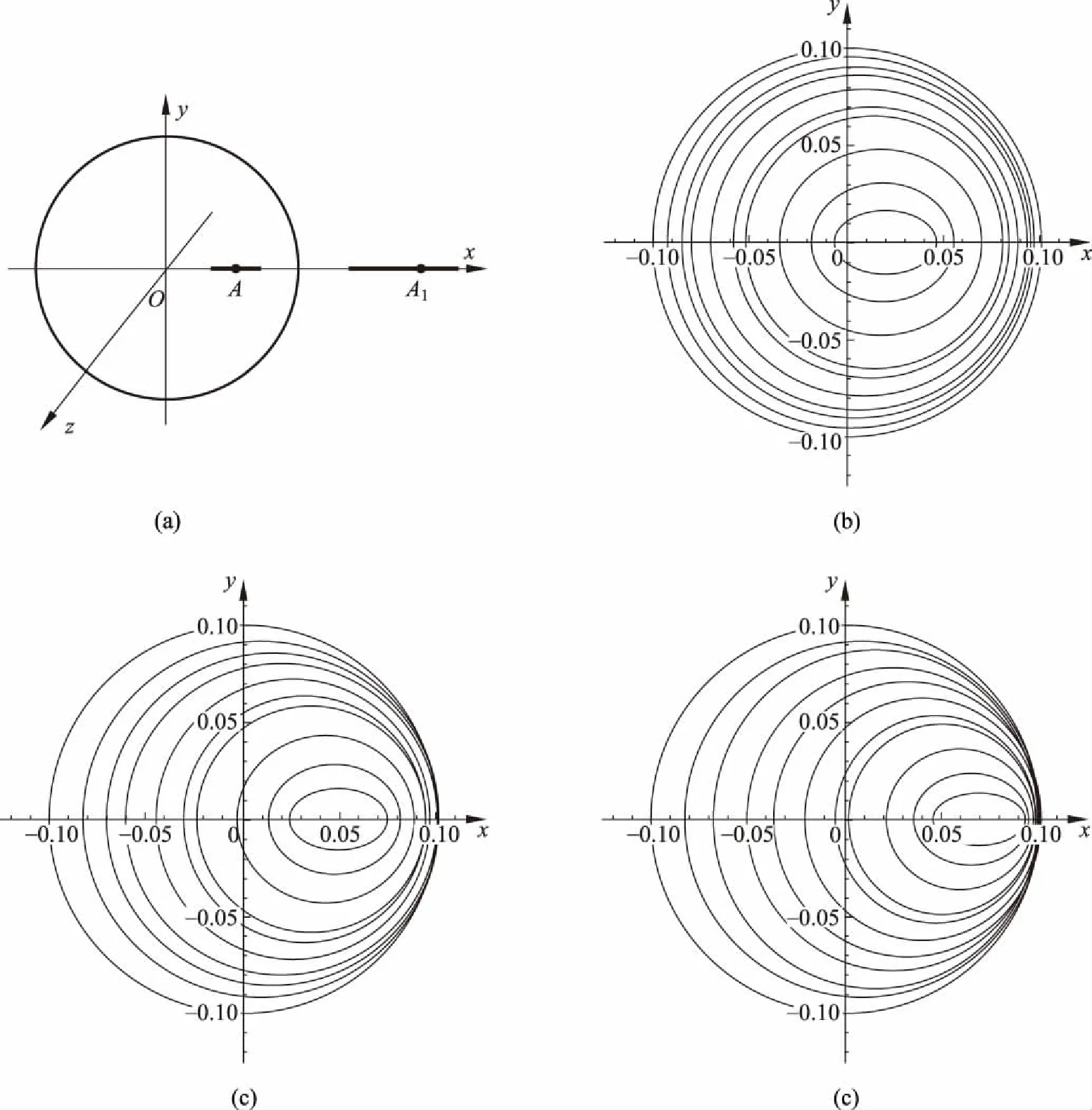
如圖1 (a) 所示,設導體球殼內徑為R,外徑為R′(R′>R),在球殼內距球心距離為d(d 電磁學理論中的鏡像法[3]是指:設半徑為R的導體球外有一帶電量為q的正點電荷,它到球心的距離為x(x>R),它的電場會在導體球面上產生感應電荷,當處于靜電平衡時,這些感應負電荷在導體球外空間(包括導體球表面)產生的作用效果(力學的、電磁學的等)等效于該正點電荷經導體球面反射成(虛)像于球心與正點電荷的連線上距球心距離為x′=R2/x的負電荷-q′在球外空間(包括導體球表面)產生的作用效果,其中負點電荷量為q′=qR/x。根據光路可逆原理,同樣設半徑為R的導體球殼內的有一帶電量為q的正點電荷,它到球心的距離為d(d (1) 其中R1、R2分別是P點到A處點電荷和A1處像點電荷的距離。為 (2) 及 (3) 將式(2)、式(3)代入式(1)可得: (4) 容易驗證:球殼內點電荷和球殼外像點電荷在球殼上的場強只有徑向分量,其切向分量為零: 上式證明中用到了正弦定理sinα=dsinθ/R1、sin(θ+β)=d1sinθ/R2和d1=R2/d及式(2)。 該處感應負電荷的電荷密度大小σ與此處的電場強度大小E由靜電平衡條件有: σ=ε0E (5) 其中,ε0為真空中的介電常數;E為球殼內壁上的所有感應負電荷和球殼內點電荷在該處產生的電場強度。則有: (6) 容易驗證球殼內壁感應負電荷的電量為q。 (7) 其中S表示對球殼內球面進行面積分。 下面研究導體球殼內部空間的電場。球殼內(包括導體球殼內表面)任意一點P1(x,y,z)的電勢是由球殼內點電荷、球殼內壁上感應負電荷和球殼外表面上感應正電荷的疊加,而球殼內壁上感應負電荷在殼內產生的作用效果由逆鏡像法可知,它等效于球殼外像點電荷產生的。若取無窮遠處電勢為零,則殼內任意一點P1(x,y,z)的電勢為: (8) 可進一步將式(8)化簡為 (9) 當球殼內空間的電勢確定時,由電勢與場強的關系E=-φ就可知道球殼內任一點的場強了,即P1(x,y,z)點的電場強度在直角坐標系中的分量為 (10) 由對稱性可知,內壁上感應電荷的分布及殼內部電場具有關于x軸的軸對稱性,與方位角φ無關。為了直觀地顯示在點電荷位于球心不同距離且導體球殼處于靜電平衡時,畫出了球殼內壁上感應電荷隨極角分布和殼內的不同電值勢的分布的圖像,在圖1(b)~圖1(d)中球殼半徑取R=0.10m,在圖1(b)是內壁上感應電荷面密度隨極角θ的分布規律, 圖像中是直線的表示感應電荷面密度不隨極角變化而變化的是d=0,即點電荷位于球心處時的結果。圖線從最右邊自上而下分別對應距球心距離d=0m、0.01m、0.03m、0.05m、0.07m、0.09m反映壁上感應電荷面密度隨極角的分布。容易看出,點電荷距離球心越遠,感應電荷分布越不均勻,殼內壁離點電荷越近,電荷面密度越大,反之,就越小。同樣,球殼內的電場(電場強度和電勢)分布也具有軸對稱性,故只需研究xOy平面內電勢即可, 在圖1(c)和圖1(d)給出導體球殼接地時的等勢線,圖1(c)和圖1(d)分別對應于點電荷距離球心d=0.05m、0.09m的接地球殼內等勢線分布,兩個圖中的13條等勢線從外到內分別對應的電勢值為:φ=0、0.2q/(4πε0)、0.4q/(4πε0)、0.6q/(4πε0)、0.8q/(4πε0)、1.0q/(4πε0)、2.0q/(4πε0)、4.0q/(4πε0)、6.0q/(4πε0)、8.0q/(4πε0)、10.0q/(4πε0)、20.0q/(4πε0)、40.0q/(4πε0)。 由于殼外感應正電荷在殼內產生電場強度為零,故球殼外感應正電荷與點電荷無相互作用的電場力,所以A處點電荷與球殼內外壁上感應電荷之間的相互作用電場力就等效于A處點電荷與A1處像點電荷之間的作用力,其大小為 (11) 圖2 均勻帶電線狀體與導體球殼(a) 球殼內帶電線狀體與像線狀體; (b) d=0m時的等勢線; (c) d=0.03m時的等勢線; (d) d=0.05m時的等勢線 接下來研究沿徑向放置的均勻帶電線狀體與導體球殼內壁上感應負電荷之間相互作用下內壁上感應負電荷電荷面密度、殼內電勢和相互作用的電場力。如圖2(a)所示,設長為L,均勻帶電量為q線狀體沿徑向放置,其左端距離球心為d。當導體球殼處于靜電平衡時,在線狀體上任一點A(x1,0,0)(d≤x≤d+L)處取一微元電荷dq, 由逆鏡像法,微元電荷dq經球面成像于A1(x2,0,0) 其中x2=R2/x1(R2/(d+L)≤x2≤R2/d),其像電荷為dq′=-dqR/x1, 則整個線狀體經球面成像于球殼外,仍為線狀體,帶電就不再均勻,遵從dq′=-dqR/x1分布規律。如該微元電荷在球殼內壁上產生等量感應負電荷-dq,其內壁上任一點P(Rcosθ,Rsinθcosφ,Rsinθsinφ)電荷分布由式(6)決定。由此整個均勻帶電線狀體在球殼內壁上產生的感應負電荷在P點分布由疊加原理有: (12) 當L→0時,式(12)將變為式(6)。 利用疊加原理,可得在均勻帶電線狀體作用下內壁上產生的感應負電荷和帶電線狀體共同產生的電勢,則殼內任意一點P1(x,y,z)的電勢: (13) (14) 下面計算均勻帶電線體與球殼內壁上感應電荷相互作用的電場力。根據逆鏡像法,帶電線體與殼內壁上感應負電荷相互作用力等效于均勻帶電線體與像帶電線體之間的作用力,如圖2(a)所示,這就等效于計算同一直線上兩帶電線體之間的電場力。在均勻帶電線體A(x,0,0)點取一微元電荷dq,它經球面成像于A′(x′,0,0) (x′=R2/x),其像電荷為dq′=-dqR/x。再在殼內均勻帶電線體上任一點A1(x1,0,0)取一微元電荷dq1,則這兩個微元電荷的相互作用力大小為 (15) 對式(15)的變量x1、x積分可得: (16) 當L→0較小時,可將上式中的對數展開 (17) 將式(17)代入式(16),當L→0時,上式變為式(11)。或直接用Mathematica數學軟件中求極限指令對求極限式(14)也得到相同結果。 在圖1(b)~圖1(d)中畫出了在接地球殼內沿徑向放置的均勻帶電細棒作用下且導體球殼處于靜電平衡時殼內的不同電勢值的分布的圖像,圖中球殼半徑仍取R=0.10m,細棒長L=0.04m,圖2(b)、圖2(c)和圖2(d)這3個圖中沿徑向放置的帶電細棒最近端距球心的距離分別為d=0m、0.03m、0.05m,圖中10條等勢線從外到內分別對應的電勢值為:φ=0、0.5q/(4πε0)、1.0q/(4πε0)、1.5q/(4πε0)、2.5q/(4πε0)、4.0q/(4πε0)、5.0q/(4πε0)、10.0q/(4πε0)、20.0q/(4πε0)、40.0q/(4πε0)。 本文根據光學中光路可逆性原理,將電動力學理論中的鏡像法拓展運用,并利用Mathematica數學軟件,研究了導體球殼內點電荷作用下,球殼內壁上感應電荷的分布和殼內空間的電勢,并計算了點電荷與內壁上感應電荷之間的相互作用力,并繪出感應電荷的分布和球殼電勢的等勢線的圖像。運用這一方法進一步計算了在殼內連續帶電線狀體作用時殼內壁上感應電荷分布,球殼電勢的等勢線等。本文采用逆行思維方法對物理研究及教學有一定的理論價值。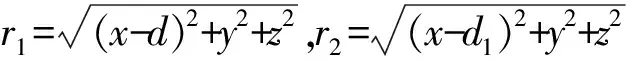
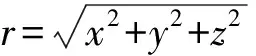
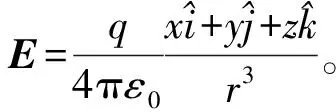
2 沿徑向的均勻帶電線狀體作用下殼內的電場
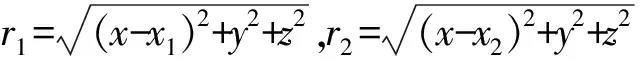
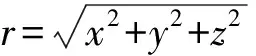
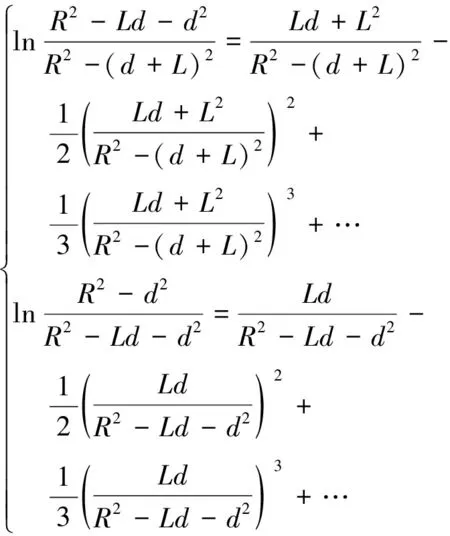
3 結語

