思維導圖在高中數學課堂教學中的案例及分析

韓 婷

(寧夏六盤山高級中學 750002)

在高中數學的學習中，各個章節之間看似分散，但各個知識點之間密切相連.基于此，在高中數學課堂教學中，必須要充分發現高中數學中各個章節知識點的聯系，并采取有效的措施，促使學生在學習的過程中，將各個數學知識點聯系到一起，進而促使學生利用數學知識解決生活中的常見問題.基于此，教師在高中數學課堂教學中，必須要充分借助思維導圖這一有效的形式，完成高中數學知識體系的構建，并在此基礎上完成學生發散性思維的培養，進而全面提升高中數學的課堂教學效果.

一、思維導圖與高中數學課堂教學

1.思維導圖概述

思維導圖是一種非常重要的學習和思維方法，又被稱之為心智圖.該思維方式將線、文字和圖形有機結合到一起，并輔以不同的顏色，共同形成一個有效的信息，進而促使學生對思維進行記錄.思維導圖作為一種有效的思維方式，與人類大腦的工作規律是相符合的，通過該思維模式，可有效啟發人類的發散性思維，并幫助人們完成知識點的梳理、記憶等工作.同時，鑒于思維導圖的特點，將其應用到課堂教學中，還可以促使枯燥、繁雜的數學知識點，變得更加具有組織性，更有利于人們的記憶.

2.思維導圖在高中數學課堂教學中的具體應用

思維導圖作為一種有效的工具和思維模式，已經在高中數學課堂教學中得到了有效的運用.在本次研究中，筆者以“平面向量的線性運算”復習為例，對思維導圖在其教學中的具體應用進行了分析.在進行該部分內容的教學中，教師在進行課前導入的過程中，為了更好地把握課前15分鐘，充分借助學生注意力最強的時間內，提升課堂教學效果.教師就充分利用了思維導圖的形式，以平面向量作為核心，引導學生對平面向量的知識進行有效的回顧，并進行思維導圖的制作：

步驟一：讓學生拿出一張白紙，并在白紙的中心位置寫上主體概念“平面向量”.

步驟二：指導學生通過多種學習方式，以“平面向量”概念作為中心，遵循學生的認知能力和思維，拓展出“基本概念”、“基本定理及坐標表示”、“向量的線性運算”、“數量積”、“應用”等一級類目，確定思維導圖的主干結構.

步驟三：當學生的思維導圖擁有一個主干結構之后，可引導學生對主干結構進行有效的補充和延申，如基本概念又可以分為向量的概念、表示方法、模、其他概念等，其中向量的表示方法可以分為有向線段、幾何表示法、字母表示法等.

步驟四：思維導圖制作完成之后，教師還要引導學生對其進行評價和分析，針對學生思維導圖中的創新部分，基于肯定和鼓勵，并對其中的不足指出進行糾正，不斷提高思維導圖的制作質量.(如下圖1所示).

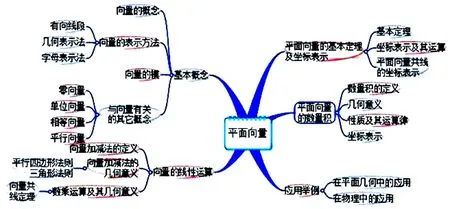
圖1

通過思維導圖在平面向量的線性運算的課前導入中的應用，學生可將以往的知識與新知識之間形成一個系統的整體，加強了新舊知識點之間的聯系，使得學生更好地進入到新知識的學習中.

二、思維導圖在高中數學課堂教學中的應用案例

思維導圖是一種高效的教學方法，對于學生自主學習和合作探究具有重要的作用.在高中數學教學過程中，教師引導學生通過思維導圖的運用，既能夠快速解決問題，也能構建起完整的知識框架，促進學生的學習效率，培養學生的數學思維能力.

例題當m為何值的時候，函數y=lg(mx3+4x+m-3)的定義域為R?

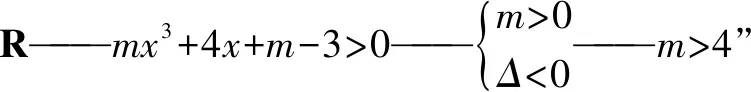
本題也可以變形為，已知函數y=lg[(a2-1)x2+(a+1)x+1]的值域為(-，+)，那么，實數a的取值范圍是多少？學生在運用思維導圖解題的時候，需要在(a2-1)x2+(a+1)x+1>0的基礎上，再分出a2-1≠0與a2-1=0的情況，當a2-1=0的時候，a=-1的情況不符合題意，因此舍去.

綜上所述，在高中數學課堂教學中，思維導圖具有極高的應用價值，并通過思維導圖在高中數學各個環節中的應用，進一步提高了學生對數學知識點的記憶效果，實現了學生數學學習能力的培養.基于此，教師必須要明確思維導圖的應用原則和制作方法，以更好地將其應用到高中數學課堂教學中.