例談整體思想在高中數學解題中的應用
江志海
(福建省三明市清流縣第一中學 365300)
數學思想是對數學知識和規律性技巧的綜合總結及融合應用,能夠具備一定的技巧性.靈活應用數學思想,方能夠從容解決高中階段復雜多樣的題型.整體思想是基于系統理論,通過不斷實踐驗證得出的一種具有指導性的全新教學思想,不僅是在應用數學領域,而且在進行高中數學的教學過程,整體數學思想要求教師能夠科學高效地啟發引導學生,將數學問題看作一個整體對待,從整體出發考慮解題思路,分析問題,最終得出最優解.這樣簡單化數學難題,有助于學生對題型的歸納總結,提高做題效率和正確率.
一、優化教學步驟,構建整體化課堂
高中數學教學的難點在于教師對教學思想的準確傳達和引導.傳統的數學教學通常采用由淺入深,從局部到整體的固化的教學模式和思維.引用大量例子講解來輔助學生對某概念或定理的學習,再通過不斷的鞏固練習進行掌握.但這樣的教學方法通常不具有較高的課堂效率,而且容易造成學生的學習乏味感,喪失學習熱情.站在提高教學效率的角度來看,教師可以采取提倡由整體到部分的整體化的授課方式,在新課程進行初始就應考慮到整體的教學進度進行課堂設計.從最開始的提出問題,可采取設置懸念,激發同學們的學習興趣,對教學方法進行合理引導,再給學生指出知識骨架,給出本節課的核心知識點,條理化學習內容,將課堂主動權還給學生,讓學生通過已給的知識框架進行整體把握,自己尋找補充具體的知識點詳細內容,這樣能夠有效做到從整體到局部的知識的講解和概念的灌輸.比如在數學集合的學習過程中,教師可以給學生講解集合基本概念后,引導學生積極探索集合的性質,通過設計合理的學習教案,讓學生從例題中體會集合的本質意義.最終進行歸納總結,明確本節知識點,如集合的確定性、無序性和互異性,這樣不僅使學生知識點掌握得更加充分,也為學生自主解決實際集合問題打下牢固基礎.
二、樹立正確解題思路,構建數學整體思想
1.整合新舊知識,建立整體思想
學生在進行新知識的學習時,必須能夠及時回顧,同時做好歸納總結,與已掌握的知識進行聯系,對新舊知識進行全面的整合應用,才能夠真正做到觸類旁通.高中數學本就知識點繁雜,遇到較難的題目時,教師要注意引導學生不在細節問題上過分糾結,不鉆牛角尖.許多問題可能乍一看條件不足,無法解決,然而實際上換一個角度重新審題,嘗試將題中所給的多個條件加以整合聯系,運用整體化的思想進行分析,往往能夠找到合適的解題方法,最終得出正確答案.高中數學的知識點眾多,需要學生對學過的知識進行熟練的掌握應用,比如各類公式和定律,都需要整體化的綜合應用,尤其在高三總復習期間,遇到的數學題大多屬于綜合應用類型,沒有形成整體化的數學思想就無法適應節奏.在計算三角函數相關問題時,對于一些不常用的角度,比如22.5°,就需要學生從整體出發,運用所學習的三角函數公式和常見的三角函數數值,將22.5°和45°進行聯系,找出規律,結合學過的正弦余弦定理,最終得出計算結果.如果按照常規的方法進行計算,很難得出正確答案,這時候就需要整體化的思維對問題進行整體變形,簡化難題.
2.化繁為簡,建立整體代換思想
整體代換的消元思想是高中數學解題思路的重要組成部分.在具體應用時,可以將若干個公式看作一個整體或變形后以整體代入另一公式中,減少單個未知變量,將原本計算復雜的公式變得更加清晰富有條理,簡化解題過程.具體多應用于多項式的計算,或是題目中含有大量未知數的式子時,可以采取換元法簡化題目進行解題.
3.采用整體合并思路解決問題
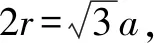
三、塑造良好的班級學風,整體化學習過程
高中數學的很多問題會有很多看起來較為刁鉆的解決思路,或者說經常存在一題多解的情況.這時就需要學生加強整體合作學習,多進行交流,集思廣益.學生之間遇到不懂的難題,可以進行小組討論,或在班內進行交流.教師需要進行積極的引導和組織,讓學生相互發言,各抒己見,共同探討,找到最優解.由于學生個人素質不同,學習能力不同,教師需要設計適當的討論活動,對學生進行積極的鼓勵和引導,使大家勇于交流、樂于交流,能意識到團體合作和整體學習的重要作用與意義,增強集體榮譽感,使學生能夠為整個班級的整體數學水平的提升做出個人相應的努力.
綜上所述,在高中數學的教學過程中,整體思維的應用不可謂不重要,教師要注意把握課堂的整體氣氛,優化課堂教學結構,并采用合理科學的解題思路進行引導和教學.從整體出發,將細節的填充和了解掌握交還給學生,塑造良好的學風氛圍,有意識地將整體思維滲透到每一個教學過程,如此才能真正提高高中數學的教學效率,提升學生整體解題水平和學習效率.

