用對立統一的觀點來探究函數圖象的變換
陳玉田
(福建省仙游縣第二中學 351200)
函數圖象的平移、伸縮、對稱等變換在中學數學里扮演了一個特殊的角色,為便于掌握,有些教輔總結出一些變換規律,并記為“左加右減,上加下減”.但筆者認為,這些規律其實并沒有看清圖象變換的本質,帶有機械性和局限性,以為不可取;進而認為教材中討論函數y=Asin(ωx+φ)圖象的變換也甚為不妥;同時發現,用對立統一的觀點來理解、記憶函數圖象的變換更具一般性,可操作性,更能體會到數學思想的作用.下面就讓咱們一起一窺函數圖象變換的端倪,為方便見,我們分別討論平移、伸縮、對稱變換.
一、平移變換
先討論把函數y=f(x)所表示的圖象向左平移k(k>0,以下均同)個單位后,要如何改變其表達式?假定點A(a,b)是函數上一點,那么圖象向左平移k個單位后,觀察坐標系可知點A移到了相應點A1(a-k,b),顯然,平移后的函數為y=f(x+k).即是把表達式中x變為x+k,注意到k>0,且坐標系的x軸為左負右正,這不就是我們常說的“左加右減”么.
辯證法認為,世上萬物都是對立且統一的.上文中“負移正加”這種現象也是一種對立統一,那么它是偶然的呢,或是必然?深入思考:把圖象向左(其實質是沿x軸負方向)平移k個單位,這時候,在對應法則不變情況下,取較小的數(因假定k>0,故有此說)就達到了原來的效果,因此,要把y=f(x)改為y=f(x+k).換個說法,用加上一個數去克服向左平移而導致自變量變小的矛盾.同樣,把圖象y=f(x)向右平移k個單位應是y=f(x-k);而把圖象y=f(x)向下平移k個單位,其實質是沿y軸負方向平移k個單位,依上述對立原理,應當改變函數表達式中的y為y+k,即改為y+k=f(x).故我們有:
定理1(函數圖象平移變換定理)函數y=f(x)的圖象沿x軸平移改變x,沿y軸平移改變y,且沿負方向平移k個單位就加上k,沿正方向平移k個單位就減去k.
具體說就是:若圖象y=f(x)左右平移時(其實質是沿x軸平移),要改變表達式中的x,且遵照“往負向移用加,往正向移用減”的原則;若圖象y=f(x)上下平移時(其實質是沿y軸平移),要改變表達式中的y,也遵照“往負向移用加,往正向移用減”的原則.用口訣可記為:左右變x,上下換y,左加右減,下加上減.
分析幾道例題:
例1函數y=2x+1的圖象向右平移1個單位后是____;向下平移2個單位后是____.
分析:向右,就是沿x軸,要改變x,并且是正方向,用減.即x→x-1.向下,就是沿y軸,要改變y,并且是負方向,用加,即y→y+2.
解新函數分別是:y=2(x-1)+1,即y=2x-1;y+2=2x+1,即y=2x-1.切記,分別是用x-1去代替原來式中的x,用y+2去代替原來式中的y.
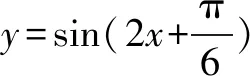
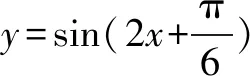
例3 函數y=3x2-2x+1的圖象向左平移1個單位后,再向上平移2個單位后得到____.
分析按常規要先配方.其實,毋須如此費事,由定理1:向左平移1個單位,就是將所有的x→x+1;向上平移2個單位,就是將所有的y→y-2.
解平移后得到y-2=3(x+1)2-2(x+1)+1整理即得.
詳述至此,細心的讀者會發現,這里不過是將原規律的“上加下減”改為“下加上減”.可是,莫小看這一變動,它體現了x、y兩條不同坐標軸的對立統一,具有普遍性,自然應適用于伸縮變換.我們知道,教材中討論y=Asin(ωx+φ)時,A>1與0<ω<1都用伸長變換,這種不一致必然給我們的理解與記憶帶來麻煩和負擔.那么,對伸縮變換能否也淡化x、y的不同,從而將它們統一起來呢?答案是肯定的.
二、伸縮變換
考慮把圖象y=f(x)變換為圖象y=Af(kx)(A>0,k>0).這里頭含有兩種變換:①x→kx,②y→by,其中,b=1/A.由倍數關系要用伸縮變換,結合教材,對照平移變換的分析,利用對立統一原理不難得出:
變換①要這樣進行:圖象上所有點的橫坐標變為原來的1/k,縱坐標不變(k>1時,縮為原來的1/k;0 變換②要這樣進行:圖象上所有點的縱坐標變為原來的1/b,橫坐標不變(b>1時,縮為原來的1/b;0 需要指出的是,這里作了b=1/A,使得y軸上的伸縮變換用b來刻畫,就與x軸上的伸縮變換高度一致,同時也體現了對立思想:大于1是縮短,小于1是伸長.故有: 定理2(函數圖象伸縮變換定理)若函數y=f(x)圖象上各點的縱(橫)坐標不變,橫(縱)坐標變為原來的1/k,就相應地改變表達式中的x(或y),且遵循倒數原則:x→kx(y→ky).即:y=f(kx)(或ky=f(x)).反之亦真. 可記為:橫x縱y,小伸大縮(大小相對1而言).當然,可以把平移、伸縮變換合起來記為:橫x縱y,負移正加,小伸大縮,對立統一. 例4把y=sinx上所有的點的縱坐標不變,橫坐標____就可以得到函數y=sin(x/4)的圖象. 分析比較知,x→x/4. 解伸長到原來的4倍. 例5若函數y=sinx的圖象上各點的縱坐標伸長為原來的3倍,而橫坐標不變,再將其向上平移2個單位,得到____. 此外,利用兩個定理,處理平移、伸縮的次序問題那便不費吹灰之力了,如: 前文提到,這種圖象變換思想具一般性,所以定理可推廣到多元函數的圖象、曲線等變換.這時候,原來前人所總結的口訣就束手無策了.如: 例7將拋物線y2=4x向下平移3個單位,再向左平移2個單位后,得到____;將x3+y3=3axy(葉形線)上各點橫坐標不變,縱坐標變為原來的1/3,所得到的圖形為____. 解①(y+3)2=4(x+2);②x3+(3y)3=9axy. 因篇幅所限,對對稱、翻折變換不再加以討論,這里只給出結果(函數圖象或曲線對稱變換定理),請讀者朋友們驗證. 定理3-1f(x,y)=0的圖象沿y軸(直線x=0)或沿x軸(直線y=0)翻折后,得到f(-x,y)=0或f(x,-y)=0. 定理3-2f(x,y)=0的圖象沿直線x=a或沿直線y=b翻折后,得到f(2a-x,y)=0或f(x,2b-y)=0. 如前所述,這些定理也可推廣到多元函數、曲線變換等,實在是一勞永逸了. 結束本文之前,不妨請讀者們再注意文中定理之結構與幾道例題的解答,整齊劃一,在高度的嚴謹中滲透著內在和諧之美.也因如此,筆者以為,不應把函數圖象變換的x、y軸分離開來,而應積極地在看似孤立的現象中尋找聯系,尋找共同點,從而把它們統一起來,方為正道!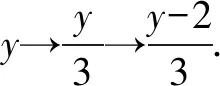

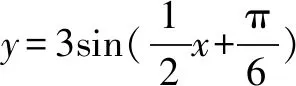

三、對稱、翻折變換


