基于威布爾分布的加速試驗剖面設計方法

王海東,蔣 剛,陳志偉,賈 斐

(1.上海航天精密機械研究所,上海 201600;2.西安電子科技大學 機電工程學院,陜西 西安 710071)

0 引言

產品壽命是評價航空航天裝備使用性能的重要指標。為準確、快速地評價航空航天產品的使用壽命,目前通常采用加速壽命試驗方法進行產品定壽。加速壽命試驗(ALT)是在合理的工程及統計假設的基礎上,采用提高工作應力或環境應力的方法來使產品快速地暴露故障,再利用加速應力下的試驗信息(失效數據、失效原因等)來外推產品在正常應力水平下的可靠性指標的一種壽命試驗方法[1]。加速壽命試驗采用加速應力進行試件的壽命試驗,縮短了試驗時間,提高了試驗效率,降低了試驗成本,其研究使高可靠長壽命產品的可靠性評定成為可能[2]。加速壽命試驗受到國內外可靠性工作人員和工程研究人員的高度重視,且已被廣泛應用于機電產品、半導體材料、武器裝備及航空航天等實際問題中[3-7]。

加速壽命試驗的類型很多,按照應力施加方式的不同,一般分為恒定應力加速壽命試驗、步進應力加速壽命試驗、序進應力加速壽命試驗3種基本類型[8]。在NELSON[9]提出的累積損傷模型基礎上,我國學者研究了不同分布類型下步進加速試驗數據處理方法。序進加速試驗數據處理方法難度較大,當前取得的研究成果相對較少,還未能成熟運用。恒定加速試驗和步進加速試驗應用較廣泛,但步進加速試驗對試驗時間和樣品數量需求更低,試驗效率較高,已成為產品定壽試驗的應用趨勢。而二參數威布爾分布作為一種連續分布,可以很好地擬合各種類型的試驗數據,因此被廣泛應用于各個領域,特別是可靠性領域中的壽命數據分析,因此基于二參數威布爾分布的研究一直是可靠性領域研究的熱點之一。鎂合金是實際應用中最輕的金屬結構材料,在航天航空產品領域具有廣闊的應用前景[10-11],所制造出的產品也具有更高的可靠性,同樣符合二參數威布爾分布。

1 試驗剖面優化設計

1.1 設計變量

1.1.1 確定試驗剖面

為了便于分析,將對簡單三步進加速壽命試驗剖面進行研究。三步進加速壽命試驗剖面如圖1所示。圖中：粗黑線表示試驗載荷施加方式;Tm為不改變失效機理的最大溫度應力,可根據少量摸底試驗或仿真確定;tc為試驗截尾時間,可根據工程經驗或者少量摸底試驗確定;T1和T2為加速溫度應力;t1,t2為應力轉換時間。除此之外,產品正常工作溫度應力為T0。

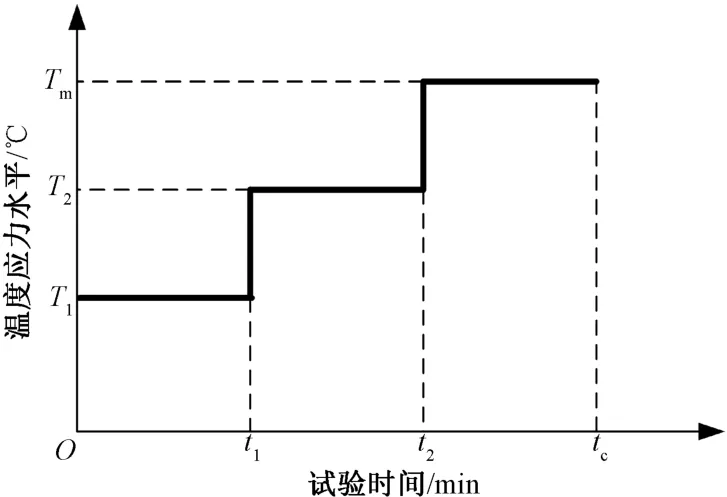
圖1 三步進加速壽命試驗剖面Fig.1 Three-step accelerated life test profile

1.1.2 模型歸一化

由于參數較多,不便于分析。為了簡便計算,且使各參數的取值與優化模型結果之間的關系模型更具一般性,需對模型進行標準化處理。

1)應力水平標準化

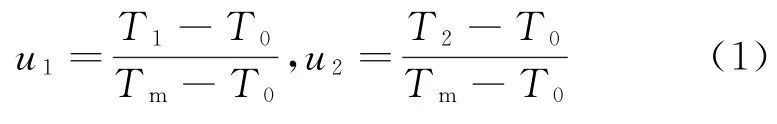
已知正常工作應力水平為T0,最高加速應力水平為Tm,令則加速應力水平T1和T2轉化為標準應力水平u1和u2。

2)應力轉換時間標準化

已知試驗截尾時間tc,令

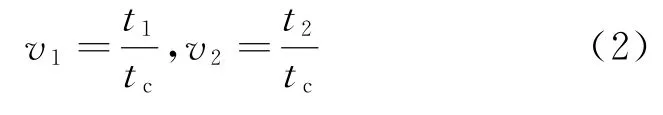
則應力轉換時間t1和t2轉化為標準應力轉換時間v1和v2。

1.2 約束條件

針對三步進加速試驗的設計變量有4個,分別為加速應力水平u1和u2,以及應力轉換時間v1和v2。對應的約束條件有

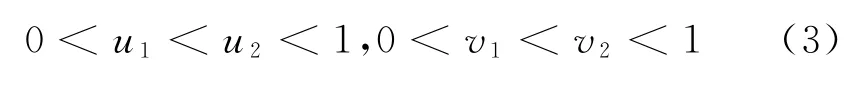
1.3 目標函數

1.3.1 確定分布函數

產品在不同應力水平下的壽命服從同一分布函數,且試驗中所有隨機試樣都具有統計獨立性。在常見產品壽命模型中,主要有指數分布、正態分布和威布爾分布,其中威布爾分布模型的應用較為廣泛,因為威布爾分布模型具有多變的函數形態,能夠很好地擬合各類數據。威布爾分布作為一種連續的概率分布模型,有近半個世紀的應用和研究歷史,在機械可靠性工程中得到了一定的應用,二參數和三參數分布形式是威布爾分布的基本形式。常用的二參數威布爾分布的累積失效分布函數和概率密度函數分別為

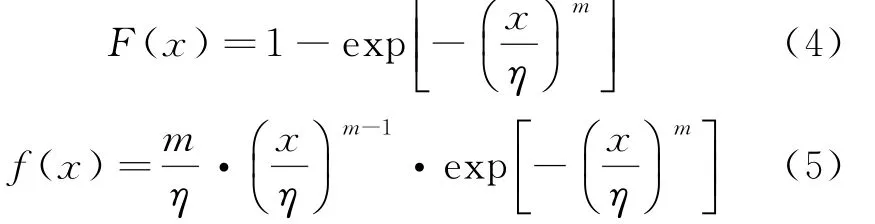
式中：x為失效時間;η為尺度參數,η＞0;m為形狀參數(根據工程經驗,0.5≤m≤5)。

為了使產品在不同應力水平下的失效機理保持一致,需假定產品在不同應力水平下分布函數的形狀參數保持不變,即二參數威布爾分布的形狀參數m保持不變。

1.3.2 確定加速模型

加速壽命試驗的實質：當產品壽命特征處于高應力水平下時去外推產品處于正常應力水平下的壽命特征,其推導關鍵在于建立壽命特征與應力水平之間的數學關系,這種關系被稱為加速模型或加速方程。常用的單應力加速模型有Arrhenius模型、逆冪律模型、Eyring模型和廣義Eyring模型。本文考慮的加速應力只有溫度,故采用Arrhenius加速模型,即

式中：T為環境溫度,℃;Ea為激活能,e V;k為玻爾茲曼常數,值為8.617×10-5e V/K;A為未知常數。

將式(6)兩邊分別取對數,有

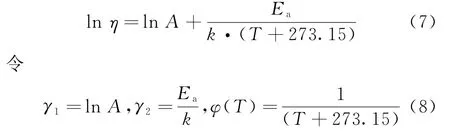
可將式(7)轉換成對數線性關系式,即

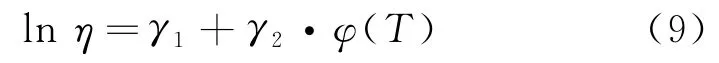
式中：γ1,γ2為未知常數;φ(T)為跟溫度應力有關的函數。

1.3.3 構建累積失效模型

NELSON累積失效理論(CE模型),假設產品的剩余壽命僅依賴于當時已累積失效的部分和當時的應力水平,與累積方式無關。這一假定是NELSON根據物理原理提出的。如果產品的壽命分布為F(t),則該假定的數學含義是：某產品在應力水平Si下的工作時間為t i,則t i內產品的累積失效概率為F i(t i),相當于在應力水平Sj下工作時間為tj時產品的累積失效概率F j(t j),即F i(t i)=F j(t j)。根據這一假定,可對不同應力水平下的壽命數據進行折算。

根據NELSON 累積失效理論,由F1(t1)=F2(τ1),得

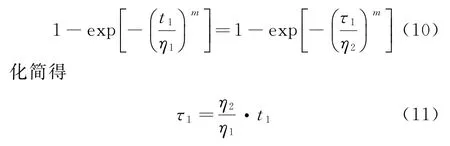
同理,由F2(t2-t1+τ1)=F3(τ2)得

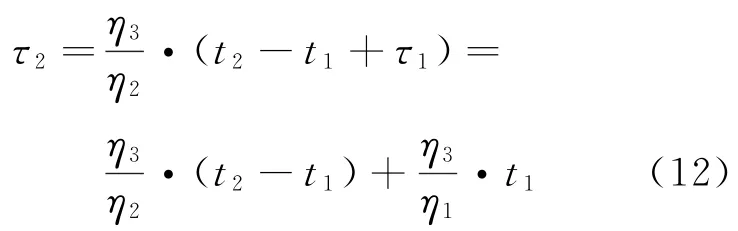
式中：τ1為在溫度應力水平T1下試驗t1時間換算到溫度應力水平T2下的累積等效試驗時間;τ2為在溫度應力水平T2下試驗(t2-t1+τ1)時間換算到溫度應力水平Tm下的累積等效試驗時間。

因此,試件失效時間X的累積分布函數為

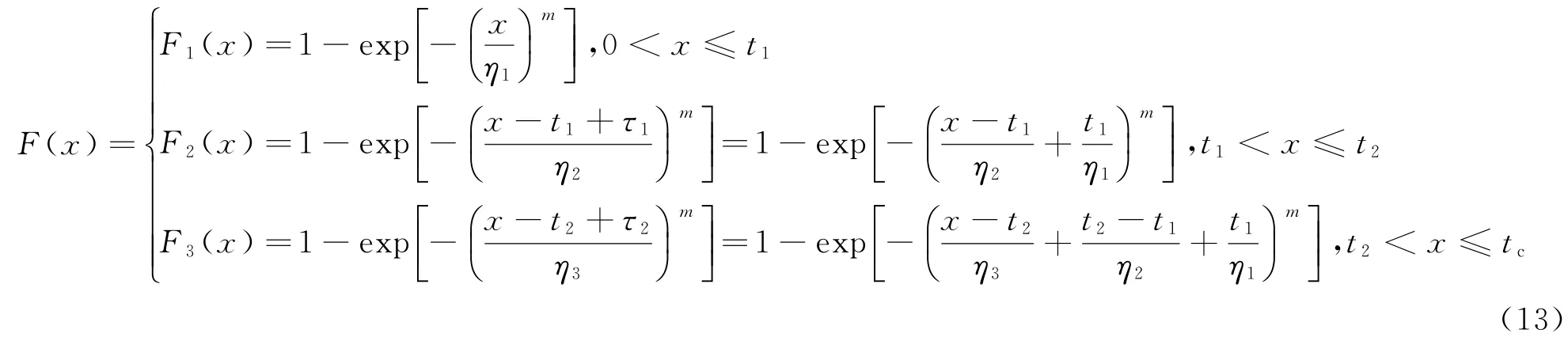
對應的概率密度度函數為

式中：F1(x),F2(x),F3(x)分別為在溫度應力水平T1,T2,Tm下的分布函數;f1(x),f2(x),f3(x)分別表示在溫度應力水平T1,T2,Tm下的概率密度函數;η1,η2,η3分別為在溫度應力水平T1,T2,Tm下的尺度參數。同時滿足

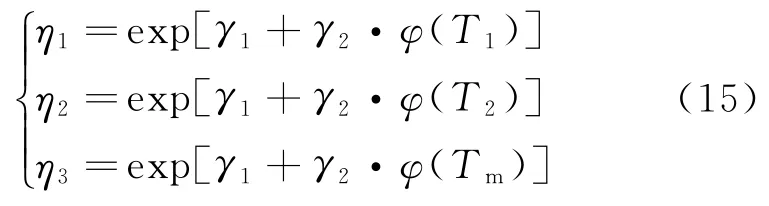
1.3.4 模型參數估計

由于加速試驗普遍存在試驗截尾、失效模式不確定等問題,因此突發型失效模式數據通常是非完整數據。極大似然估計(MLE)不僅適用于完整數據,同時適用于非完整數據,因此,選擇MLE 對加速試驗突發型失效模式數據進行統計分析。

假設第i個樣本在時間xi失效,定義3個指示函數

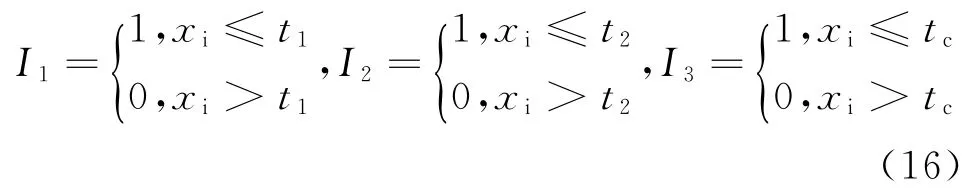
則第i個樣本的對數似然函數L i為

當投入試驗的樣本量為n時,則所有樣本的的對數似然函數L為

解L的一階偏導數方程組,由

1.3.5 分位數壽命估計

根據加速模型公式,可以計算得到在正常溫度應力水平T0下的尺度參數η0的估計值為

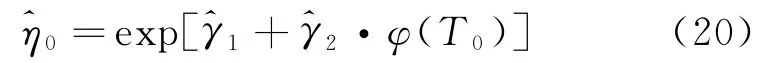
從而得到在正常溫度應力水平T0下的累積分布函數為

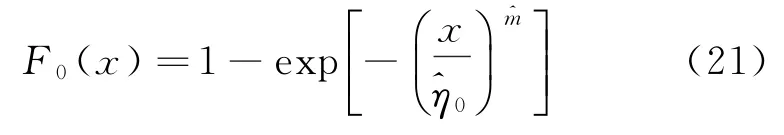
故產品的P階分位數壽命x P的MLE估計值為

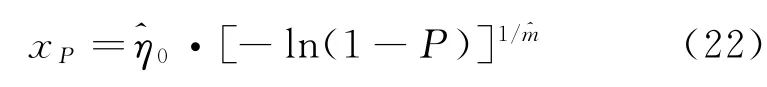
1.3.6 優化準則與漸進方差

1)優化準則

對于具有可靠性高且壽命長的產品,做加速壽命試驗時,通常選取產品在正常應力下P階分位壽命MLE估計值的漸進方差作為其可靠性壽命特征量。為提高該特征量估計精度,并減少試樣數量、縮短試驗時間,需要優化加速壽命試驗方案。在正常應力下,以產品P階分位壽命MLE 估計值的漸進方差最小為準則,對加速壽命試驗方案進行優化。

2)壽命的漸進方差

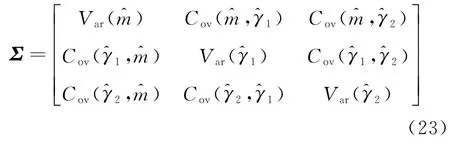
一般協方差矩陣難以求得,根據MLE 估計理論,協方差矩陣Σ與信息矩陣F為互逆,即Σ=F-1,故通常采取對信息矩陣求逆來求得協方差矩陣。而信息矩陣可由n個樣本的對數似然函數對各模型參數的負二階偏導數矩陣的數學期望求得,有

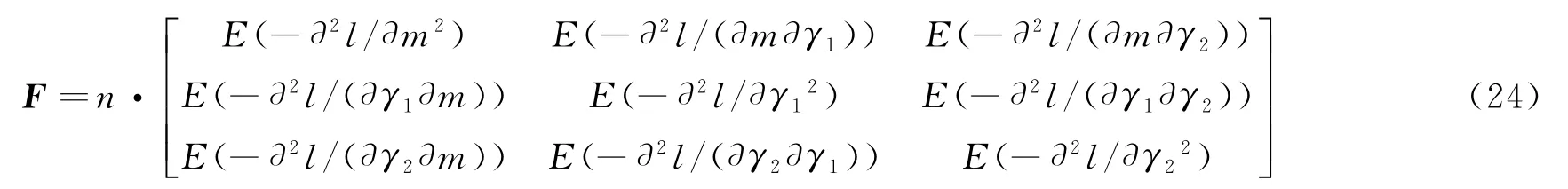
通常,極大似然估計量具有漸進無偏性和漸進正態性,故可得到在正常溫度應力水平T0下,產品P階分位數的對數壽命的漸進方差為

地鐵供電系統中剛性接觸網常見故障和防范措施解析……………………………………………………… 鐘人正（7-72）

式中：H為一階偏導矩陣,即

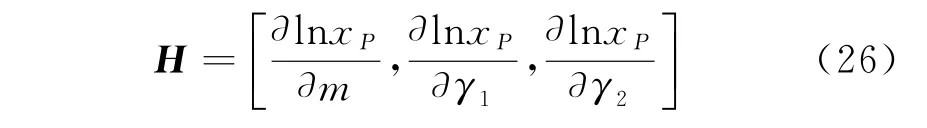
由式(1),(2)得

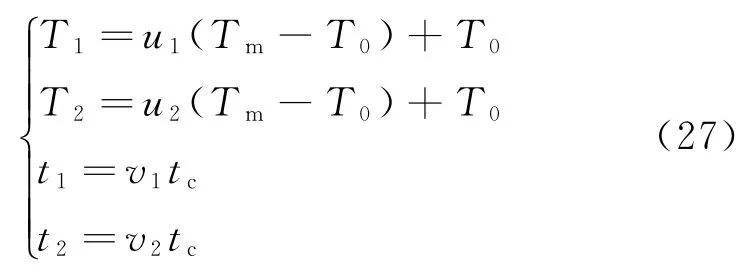
再將式(27)代入式(25)中,可得到只與4個設計變量u1,u2,v1,v2有關的漸進方差表達式。

經過推導計算,信息矩陣F里面的元素過于復雜,無法求出具體的定積分表達式,故采用數值積分的方法進行近似求解。考慮到使用數值積分需要已知積分區間,且整個推導過程中涉及到諸多變量替換,同時存在約束條件,故考慮使用非線性規劃算法進行優化求解。而經典非線性規劃算法大多采用梯度下降的方法求解,需知道顯式的函數表達式,顯然不適用,故綜合考慮下決定使用隨機Monte-Carlo模擬的方法進行優化求解,求使漸進方差取得最小值所對應的優化變量

2 仿真算例

結合部分工程經驗,假設參數真值為m=2,γ1=10,γ2=2 300;溫度應力水平分別為T0=20 ℃,T1=50 ℃,T2=80 ℃,Tm=110 ℃;試 驗 時間為t1=40 min,t2=80 min和tc=120 min;試驗樣本量為n=40。

現以產品在正常溫度應力水平T0下的對數中位數壽命估計值的漸進方差為優化準則,以加速應力水平u1,u2和應力轉換時間v1,v2為設計變量,進行三步進加速試驗方案的優化設計。

采用Monte-Carlo模擬的方法進行1 000次隨機尋優求解的結果為=0.33,=0.82,此時所對應的漸進方差最小值為0.11。若采用傳統均勻設計的加速試驗方案：=1/3,,此時所求得的漸進方差為0.34。

顯然,經過優化后的壽命估計值的漸進方差比傳統均勻設計的漸進方差要小,這表明經過優化的加速試驗方案比傳統均勻設計的試驗方案具有更高的估計精度。

3 結束語

為實現對高可靠性、長壽命產品在正常環境應力水平下壽命與可靠性的快速評估,本文在單應力情形下,研究了二參數威布爾分布的三步進加速試驗的優化設計理論與試驗數據的統計分析方法。通過建立Arrhenius與二參數威布爾分布試驗的可靠性統計模型,以產品在正常溫度應力水平下中位壽命估計的漸近方差最小為優化準則,給出了二參數威布爾分布的三步進加速試驗應力水平與應力轉換時間的優化設計方法,并通過與傳統均勻設計加速試驗方案的對比,表明經優化后的加速試驗方案具有更高的估計精度。采用隨機Monte-Carlo模擬的方法代替傳統非線性規劃算法進行加速試驗方案設計變量的優化求解,以解決函數表達式過于冗長、計算復雜等問題。今后將考慮基于二參數威布爾分布進行多應力(如溫度、濕度、振動等)綜合加載方式下的步進加速試驗統計分析與試驗設計優化方法研究,并考慮基于二參數威布爾分布進行多步進(即加速應力水平數大于3)情況下的步進加速試驗統計分析與試驗設計優化方法研究。