傾斜基巖條件下軌道交通振動衰減規律研究

楊金川，丁選明，瞿立明，崔春義，李錚，巫崇榮

(1.重慶大學 山城城鎮建設與新技術教育部重點實驗室；庫區環境地質災害防治國家地方聯合工程研究中心，重慶 400045；2.大連海事大學 土木工程系，遼寧 大連 116026；3.重慶市城市建設投資(集團)有限公司，重慶 400023)

軌道列車在高架段運行時，由于軌道不平順、車輛不圓度和列車軸重等激勵下引起軌道結構振動[1]，振動通過橋梁傳到橋墩，再通過樁基礎傳到土體中，從而引起地表振動。這些振動會造成周圍建筑物沉降、結構強度降低，引起墻體開裂等問題；當人體處于振動環境中時，振動會引起頭暈、精神難以集中等不適癥狀；當振源附近存在其他精密儀器時，儀器的正常使用將受到影響[2-3]。因此，軌道交通引起的環境振動問題不容小視。

據統計，山城重慶城市軌道交通中，高架部分占51.5%[4]，由高架列車引起的環境振動問題也越發突出。許多學者對高架軌道交通列車引起的環境振動進行了大量的研究。何鑒辭等[5]研究了列車通過高架橋直線段和曲線段時各自的衰減規律及其頻譜特性；李丹等[6]基于動力學理論，獲得了不同橋梁跨度、不同列車速度下產生的振動波及其在層狀土體中的衰減規律；李小珍等[7]通過實測研究和理論分析得出了高架車站不同區域的環境振動規律。高廣運等[8]采用半解析數值法建立高架橋線路地面振動模型,研究了樁直徑、樁長、樁間距和軌道不平順對地面振動的影響；Feng等[9]通過現場測試對比分析了高鐵通過路堤、涵洞、高架和過渡段時地表振動特性。Connolly等[10]通過現場試驗比較了路塹、路堤和路基面3種路基形式下軌道產生的振動水平，研究發現，路堤形式下產生的振動水平最低，路塹最高；Degrande等[11]研究了列車速度在256～314 km/h的情況下，振動強度隨振源距離的分布規律，發現地面振動在距線路20～40 m的范圍處存在一個反彈增大區。Kouroussis等[12]對布魯塞爾和巴黎/倫敦之間典型場地中由HST引起的振動進行了現場測量，研究了火車特性和土壤分層對地面振動的影響。

以上研究在振動衰減規律、振動對周圍環境影響和振動響應特性等方面取得許多有意義的成果，但大都是通過建立在均質的、無限大水平的土體中得到，地形對軌道交通振動衰減規律的影響研究尚少。考慮到山區地形的特殊性，軌道交通路線不可避免地穿越復雜地形，因此，研究地形對軌道交通振動衰減規律的影響具有重要意義。

本文通過模型槽試驗與有限元模擬研究了傾斜基巖條件下軌道交通振動的衰減規律，并分析了基巖傾斜角度、加載頻率、樁長對軌道振動衰減規律的影響。

1 模型試驗

試驗采用的土工模型槽系統主要包括模型槽、反力架系統、動力加載系統、測量系統4部分。模型槽尺寸長×寬×高為2.5 m×2 m×3 m，位于地表以下，上部設有反力架系統。試驗所用填土為粉質砂土，天然含水率為14.01%，最大干密度為1.64 g/cm3，最小干密度為1.17 g/cm3。試驗采用剛性鋼板模擬傾斜基巖地層，基巖傾角β=26.6°。采用預制鋼筋混凝土樁，樁長1.2 m，直徑106 mm。試驗使用東華測試DH5921型數據采集儀，自帶64通道，數據處理采用配套的DHDAS動態信號采集分析系統，土體表面使用東華測試研制的2D001V型速度傳感器。

1.1 試驗方案

試驗采用單樁模型，將正弦波荷載作用于樁頂，輸入荷載時程函數N=2.4+0.8 sin(2π·13t)。其中，t為時間，單位為s，荷載單位為kN。目前，許多關于軌道交通的研究均以豎向振動為主[13-14]，因此，本試驗采用測量豎向振動的速度傳感器，下文振動測試數據均為豎向振動數據。

如圖1所示，將剛性鋼板傾斜放入模型槽中固定，然后填土，并分層夯實，填土高度達到70 cm時，在槽中心處放樁固定，繼續分層填土夯實至180 cm，樁頭露出表面10 cm以便加載。平整土體表面后，將速度傳感器沿樁呈放射狀布置，各方向每30 cm布置1個，其中1#測點距離樁側8 cm，考慮距離樁側較近的與樁同心圓上地表各處的振動響應差異很小，因此，將1#測點作為所有方向的公共測點。土體表面共布置14個速度傳感器，其平面布置圖與現場布置圖分別如圖2、圖3所示。其中，傳感器沿樁徑向在α=0°、45°、90°、135°、180° 5個輻射方向布置；2#～6#、7#～11#、12#～14#測點分別在r=38、68、98 cm的圓上，r為距樁邊的距離。

實驗通過動力加載系統模擬正弦荷載，并將加載板作用于樁頭，試驗每次加載5 min，靜置15 min后進行下一次加載。

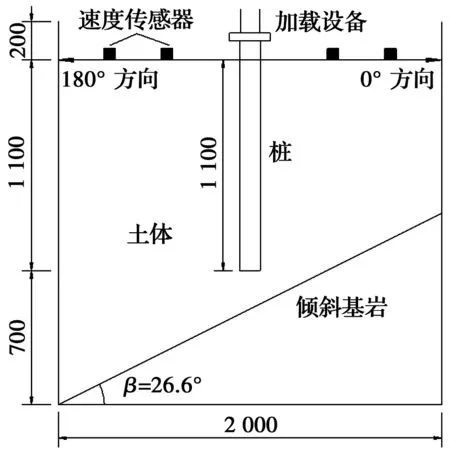
圖1 模型布置剖面圖Fig.1 Sectional view of the

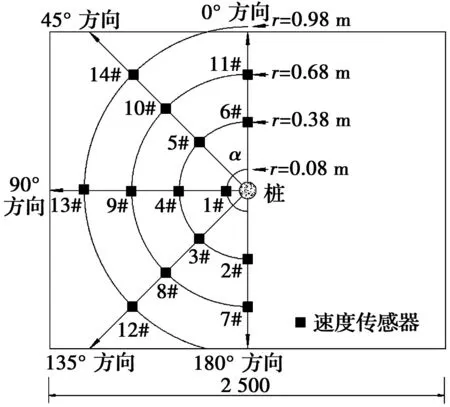
圖2 模型布置平面圖Fig.2 Plan layout of the

圖3 速度傳感器布置現場圖Fig.3 Arrangement of speed sensors in

1.2 試驗結果分析

為研究傾斜基巖條件下地面振動的衰減規律，分別進行傾斜基巖和水平基巖條件下的模擬試驗，并對比兩者差異。測得傾斜基巖工況下地表45°方向5#、10#、14#測點振動時程曲線，如圖4所示。通過傅里葉變換得到頻域分析圖，如圖5所示。

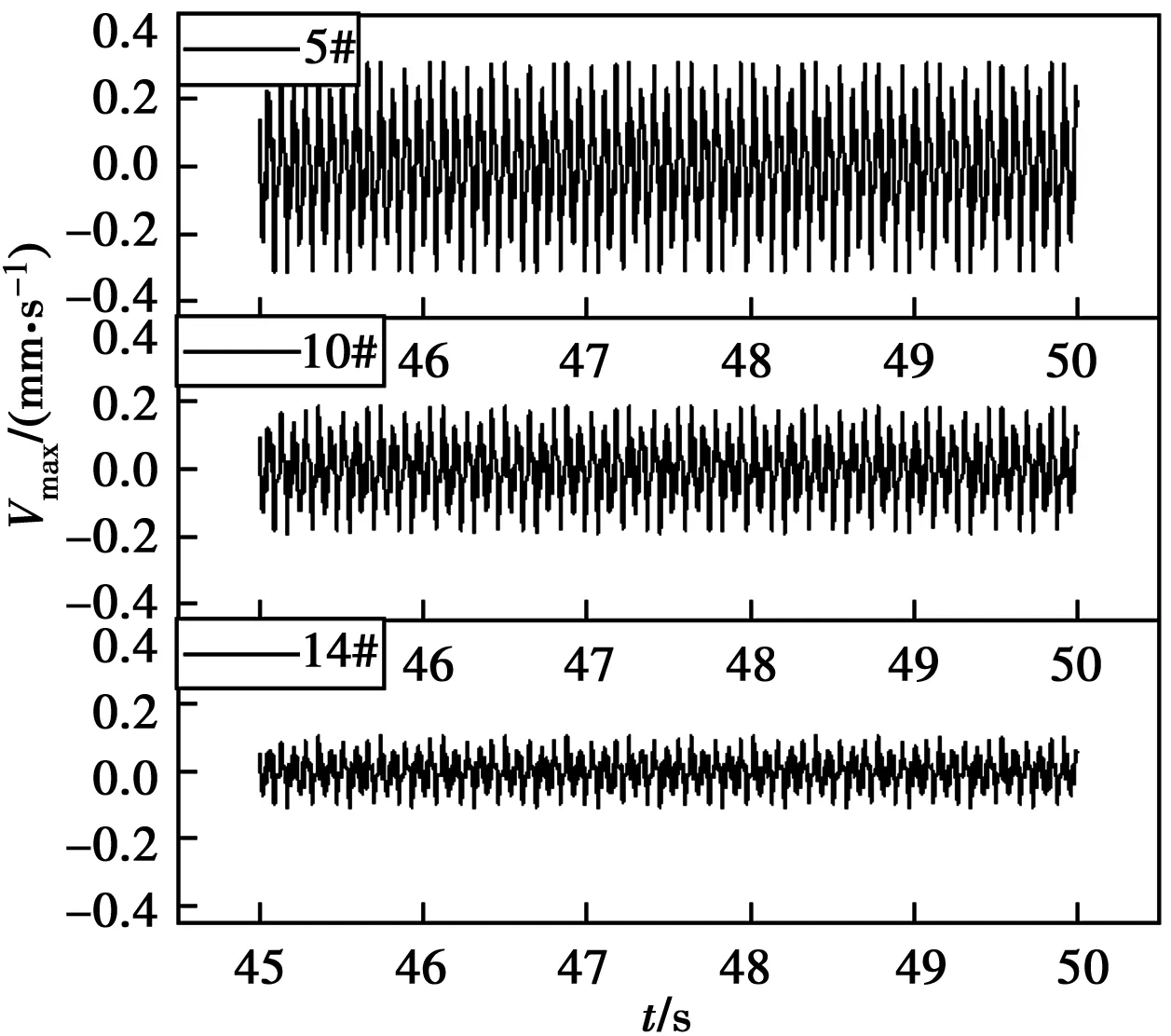
圖4 45°方向測點振動時程曲線Fig.4 Time history of measuring points in 45°

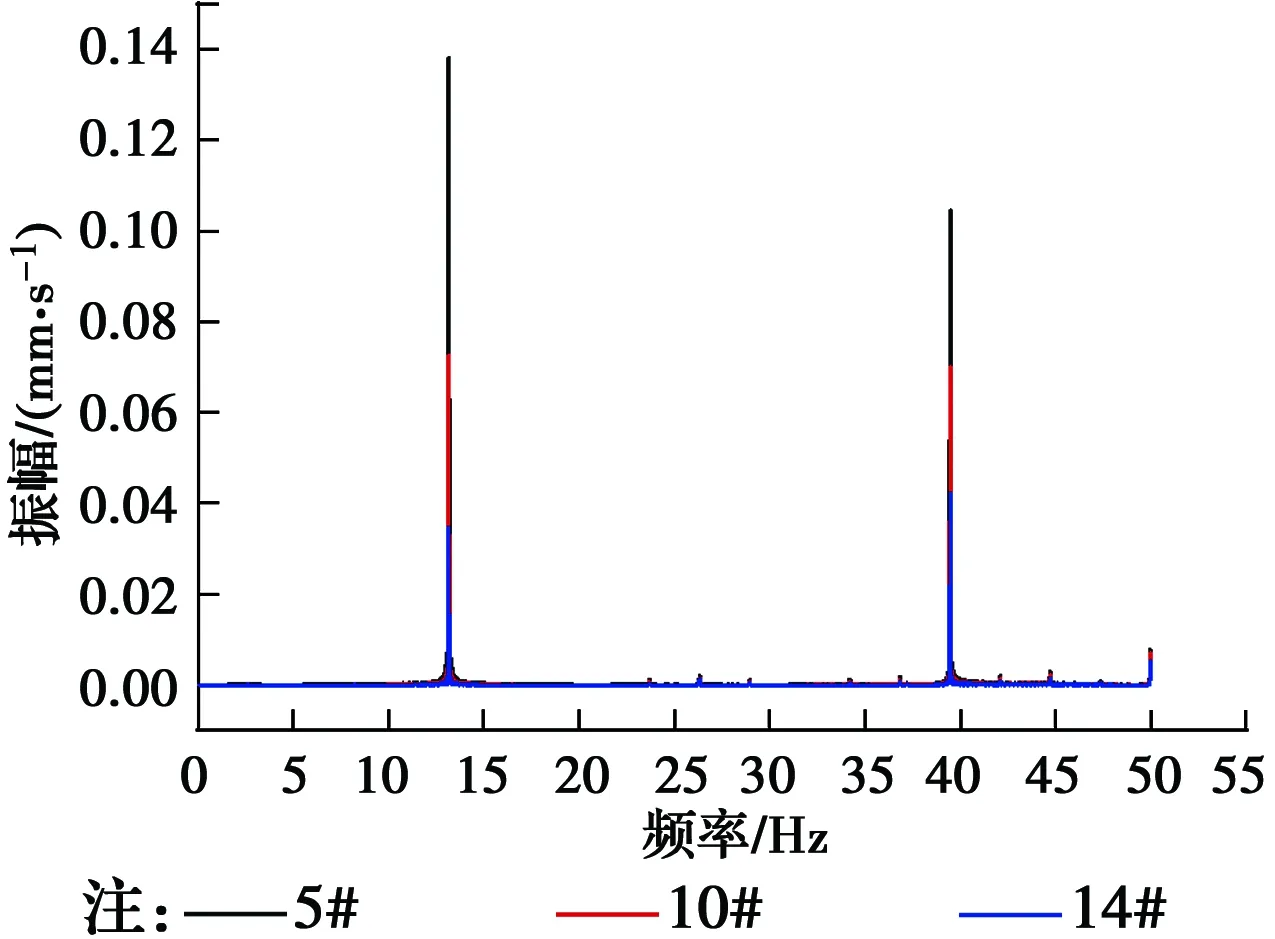
圖5 45°方向測點振動頻譜曲線Fig.5 Fourier’s spectrum of measuring points in 45°

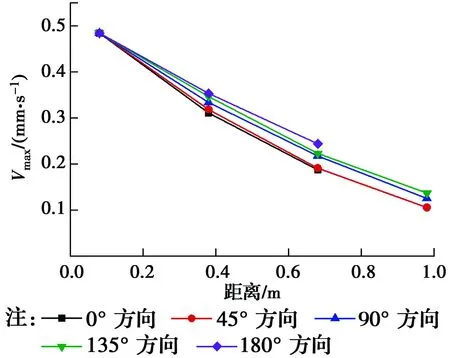
圖6 傾斜基巖條件下地面峰值速度衰減規律Fig.6 Attenuation of ground peak velocity for the

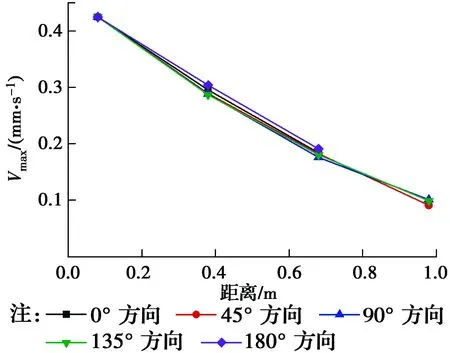
圖7 水平基巖條件下地面峰值速度衰減規律Fig.7 Attenuation of ground peak velocity for the

圖4表明，地面振動響應在一定距離范圍內隨著距離增加而減小；圖5表明，在45°方向各測點的頻譜曲線中，3個測點的頻率分布一致，優勢頻率為13 Hz，與輸入荷載頻率相同，且距樁越近速度幅值越大。

圖6、圖7分別表示傾斜基巖與水平基巖條件下地表速度峰值衰減規律，兩種工況下，振動總體衰減趨勢較為一致，呈現出先快后慢的規律。在水平基巖工況下，地表振動沿各方向衰減規律大致相同；但在傾斜基巖工況下，振動沿樁徑向衰減快慢則呈現明顯的方向性差異，振動沿0°方向衰減最為迅速，沿180°方向衰減最慢，且從0°方向到180°方向衰減速率逐漸變小。該現象可能是由于波沿傾斜基巖面反射而向傾斜面下方聚集造成。圖8為與樁邊等距離處地面峰值速度變化規律，水平基巖下，在距樁邊等距離各點上的速度響應較為一致，而在傾斜基巖條件下，距樁邊等距離各點的峰值速度從0°到180°方向逐漸增大，且兩種工況的峰值速度差從0°到180°方向呈現逐漸增大的趨勢。值得注意的是，在實驗中，當荷載頻率較大時，荷載加載瞬間地表速度響應突然增大，根據Dowding[15]的解釋，這種地面振動的增加可達到4倍，并且，當荷載頻率瞬間通過產生最大地面振動的頻率時就會發生。本文中所取的速度峰值均為穩態值。

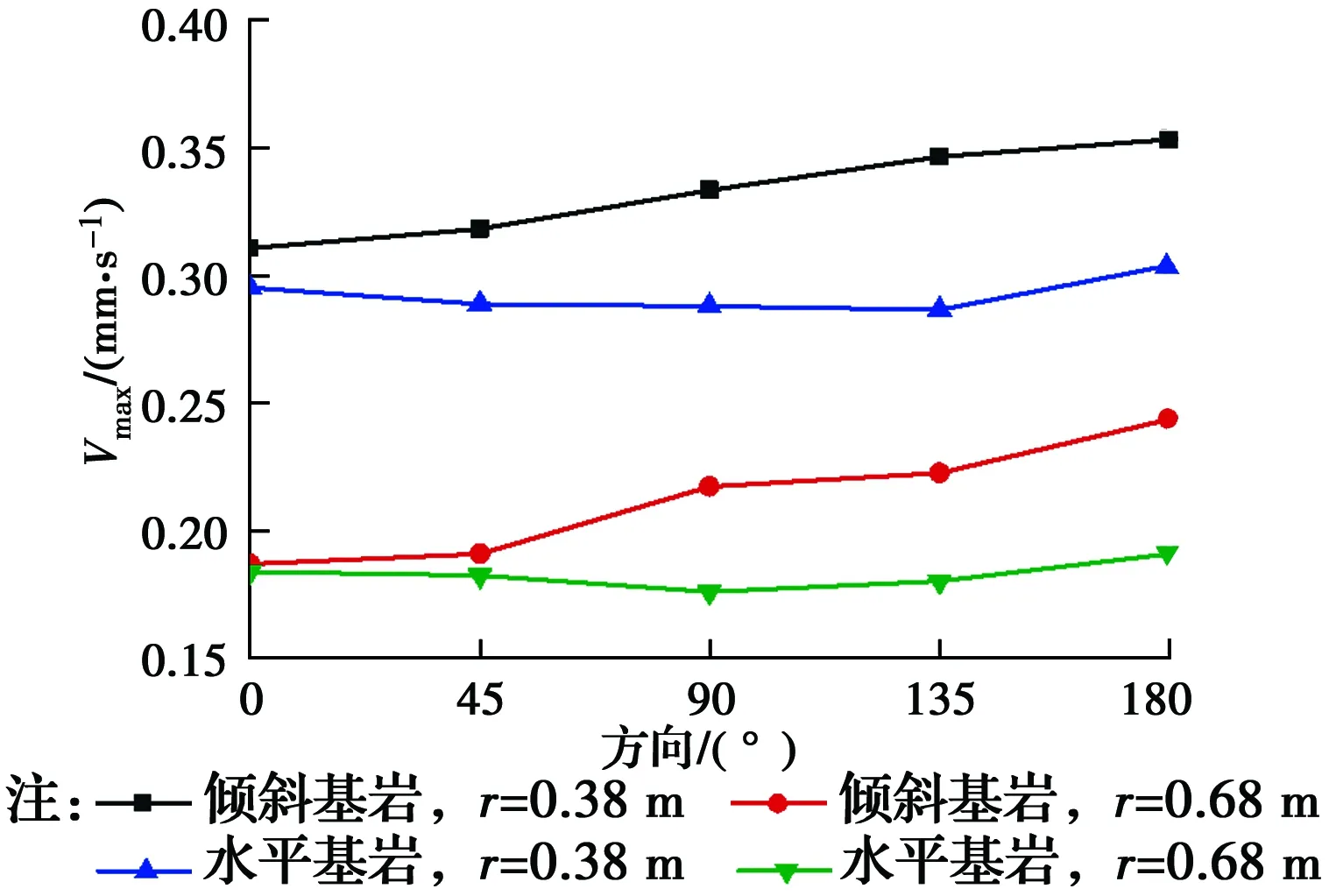
圖8 與樁等距離處地面峰值速度變化規律Fig.8 Variation of ground peak velocity at different radial

2 試驗數值驗證

2.1 數值模型建立

采用ABAQUS有限元軟件，進行三維數值模擬研究。數值模型幾何尺寸與試驗相同，土體水平面長×寬為2.5 m×2 m，土層最厚處為1.8 m，基巖傾斜角為26.6°，土體采用各向同性線彈性模型，模型應力應變表達式為

(1)

式中：土體彈性模量E=30 MPa，泊松比v=0.25；混凝土樁長1.2 m，直徑0.106 m，彈性模量E=30 GPa，泊松比v=0.17。

在有限元動力分析中，結構阻尼通常采用表示為質量阻尼與剛度阻尼線性之和的瑞利阻尼形式，即

[C]=α1[M]+β1[K]

(2)

通常α1、β1的值采用振型阻尼比ξi計算得出。如果ωi是第i階模態的固有頻率，根據振型正交條件，α1和β1與振型阻尼比之間應滿足式(3)。

(3)

在動力分析中，由于結構前幾階振型起主要作用，通常分析中根據第一振型確定阻尼，即

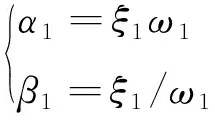
(4)

式中：阻尼比為0.05，模型一階振型頻率為22.09 Hz。

模型網格劃分采用六面體單元，在靠近樁土接觸面的位置，利用種子偏置功能進行加密，土體采用掃掠網格劃分技術，模型網格如圖11所示，土體四周采用固定邊界，底部也采用固定邊界模擬傾斜基巖。

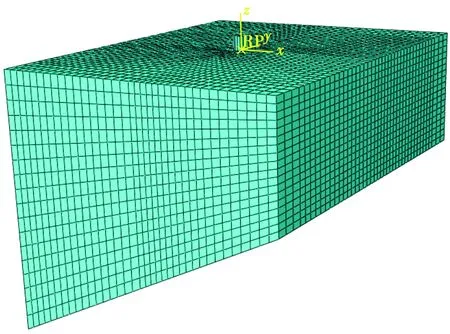
圖9 三維有限元網格Fig.9 Three-dimensional finite element

2.2 試驗數值驗證

為驗證數值模型的合理性，選取土體表面具有代表性的45°方向、135°方向數值計算結果與試驗進行對比，下面分別對比了數值與試驗的振動衰減曲線和時程曲線。

圖10(a)、(b)表明，數值模擬結果較試驗值先衰減快后衰減慢，在距樁較近測點上誤差較大，其他距離處則對應得較好，數值結果的整體變化規律與試驗結果較為一致，地表振動沿各方向衰減呈現方向差異化，從45°方向到135°方向衰減速度逐漸變慢；在距樁等距離的各方向上，峰值速度也從45°到135°方向逐漸增大。圖10(c)、(d)分別對比了2個方向的時程曲線，數值與試驗結果吻合度較好，二者時程曲線規律一致。考慮到試驗誤差，數值結果具有較高的可靠性。

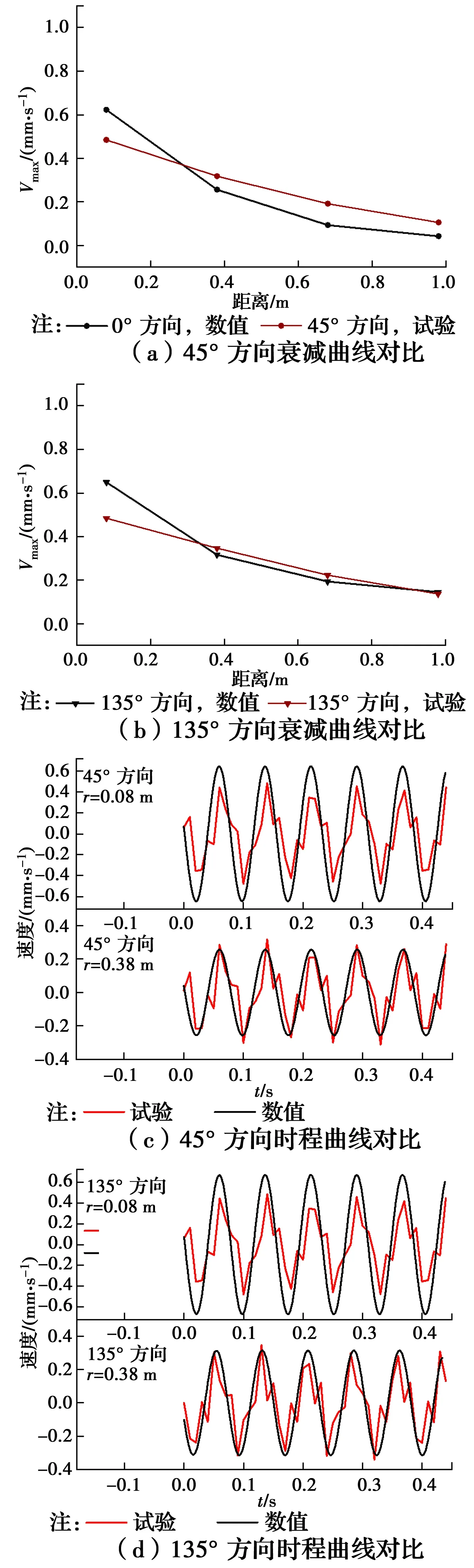
圖10 試驗與數值結果對比Fig.10 Comparison of test and numerical

3 參數影響分析

前文對比了試驗數值結果，驗證了數值模型的合理性，下面將通過數值模型來研究基巖傾斜角度、加載頻率、樁長等單一變量對地表振動衰減規律的影響，各參數取值見表1。

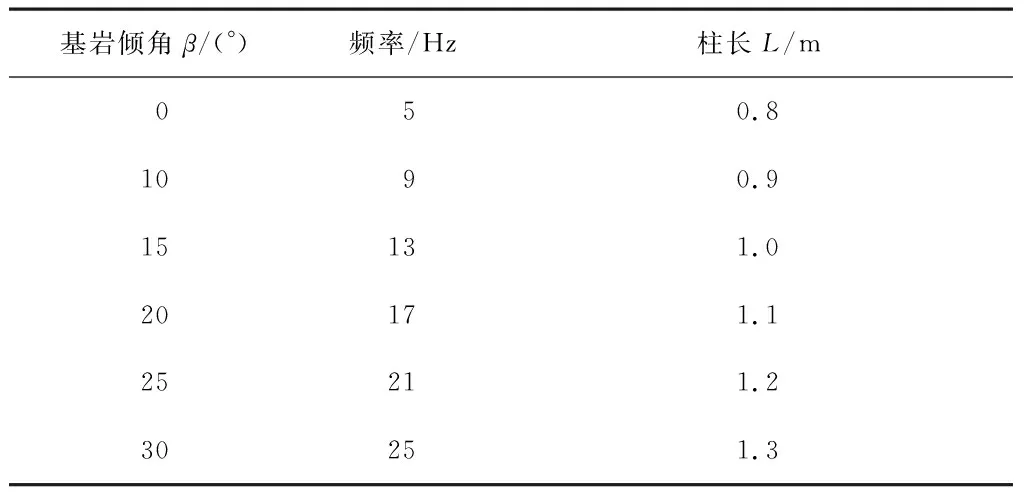
表1 各參數取值表Table 1 Parameter list

為了描述各變量對振動沿各方向衰減差異性的影響，引入歸一化值N，N為與樁同心圓上各點速度響應峰值除以圓上0°方向速度峰值歸一化得到，即

(5)

式中：Ri為同心圓上各點處速度峰值；R0為同心圓上0°方向速度峰值，再引入歸一化值N1，表示樁徑向上各點峰值速度除以樁邊第1個點峰值速度歸一化得到。

3.1 基巖傾斜角度的影響

為研究基巖層傾斜角度對振動衰減的影響規律，數值模擬中控制傾斜角度β在10°～30°之間變化，并與水平基巖層(β=0°)工況進行對比，輸出數值計算結果如圖11～圖13所示。

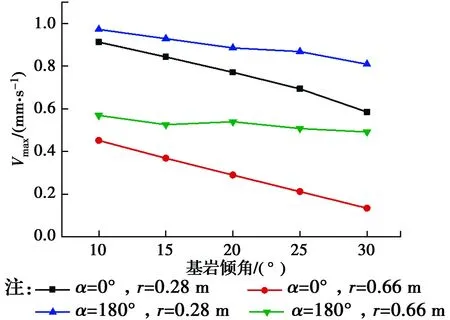
圖11 地面振動響應隨基巖傾角變化規律Fig.11 Variation of ground dynamic responses withbedrock

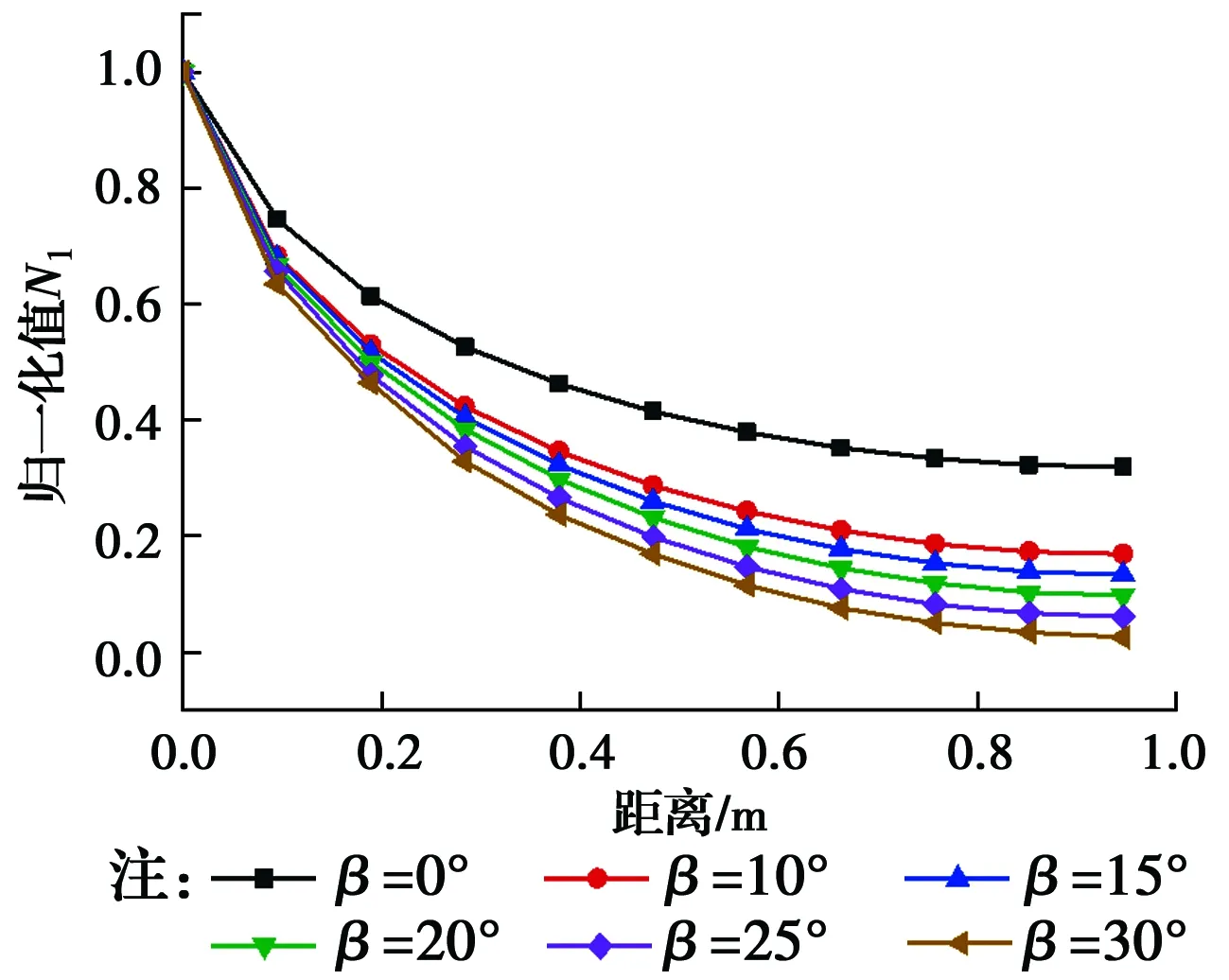
圖12 0°方向衰減曲線隨基巖傾角變化Fig.12 Variation of attenuation curve with bedrock dip in direction of

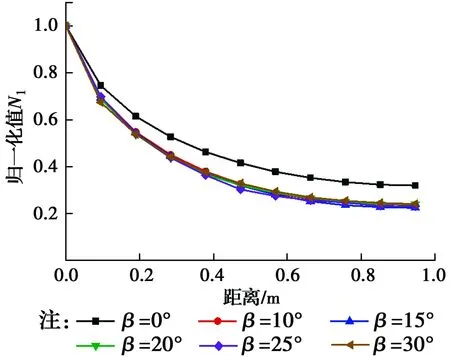
圖13 180°方向衰減曲線隨基巖傾角變化Fig.13 Variation of attenuation curve with bedrock dip in direction of

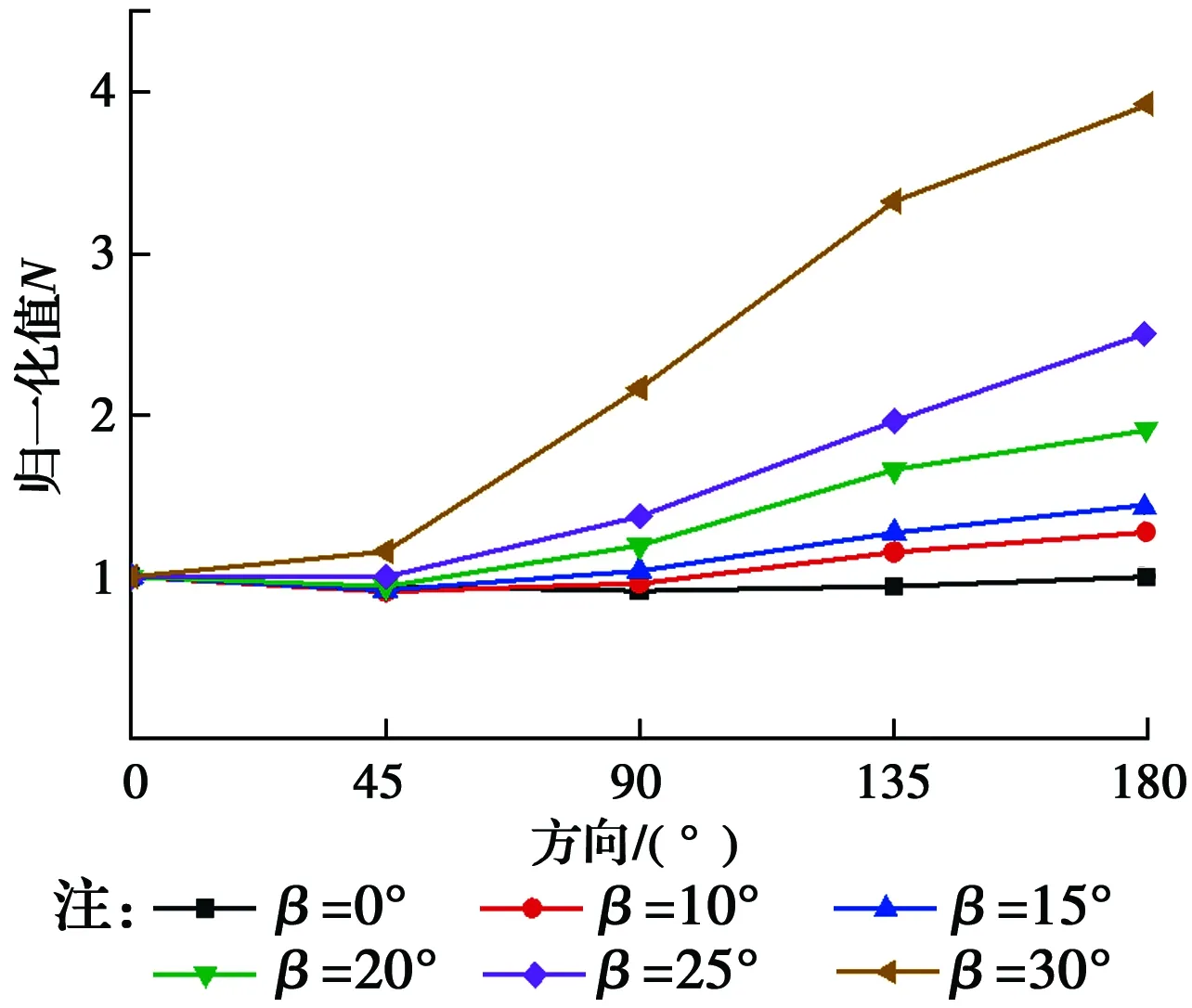
圖14 r=68 cm環線上速度響應隨基巖傾角變化Fig.14 Variation of velocity response with bedrock dip for the case of r=68

如圖11所示，基巖傾斜角度越大，地面振動響應越小，且對各方向的影響呈現出差異化。在0°方向上，地面振動速度峰值隨角度增加呈線性減小，且各距離上減小速率一致；在180°方向上，速度峰值隨角度增加則是無規律減小，且減小速率明顯低于0°方向。圖12、圖13分別表示基巖傾斜角度對0°、180°方向振動衰減的影響規律，從圖中可以得出，基巖傾斜角度變化對地表振動衰減規律也呈現差異化影響。在0°方向上，隨著基巖層傾斜角度增大，地面振動衰減速率逐漸增快，且隨傾角呈線性增加；在180°方向上，各傾斜角度下，該方向的振動衰減曲線幾乎重合，因此，該方向振動衰減規律不受基巖傾角變化的影響；在傾斜基巖的情況下，兩個方向的振動衰減速度均明顯快于水平基巖工況，可見傾斜地層對振動衰減的影響較為顯著。圖14表示地表與樁等距離處(r=68 cm)各測點振動響應差異隨基巖傾角的變化規律。當基巖傾角較小時，與樁等距離圓上各方向的振動響應差異較小，且水平基巖工況下各方向振動較為一致，差異最小；隨著傾角的增大，各方向的速度峰值差異顯著增大。從圖中看到，當傾角β=30°時，180°方向的峰值速度約為0°方向速度峰值的4倍。同時注意到，當基巖傾斜角度較小時，各方向的峰值速度最小值出現在45°方向上，隨著傾斜角度的增大，最小值則開始出現在0°方向上。

3.2 頻率的影響

保持其他參數不變，控制單一變量荷載頻率在5～25 Hz之間變化，分析荷載頻率對地表振動響應以及與樁等距離各處響應差異的影響。地表振動和各方向響應差異隨頻率變化如圖15～圖17所示。

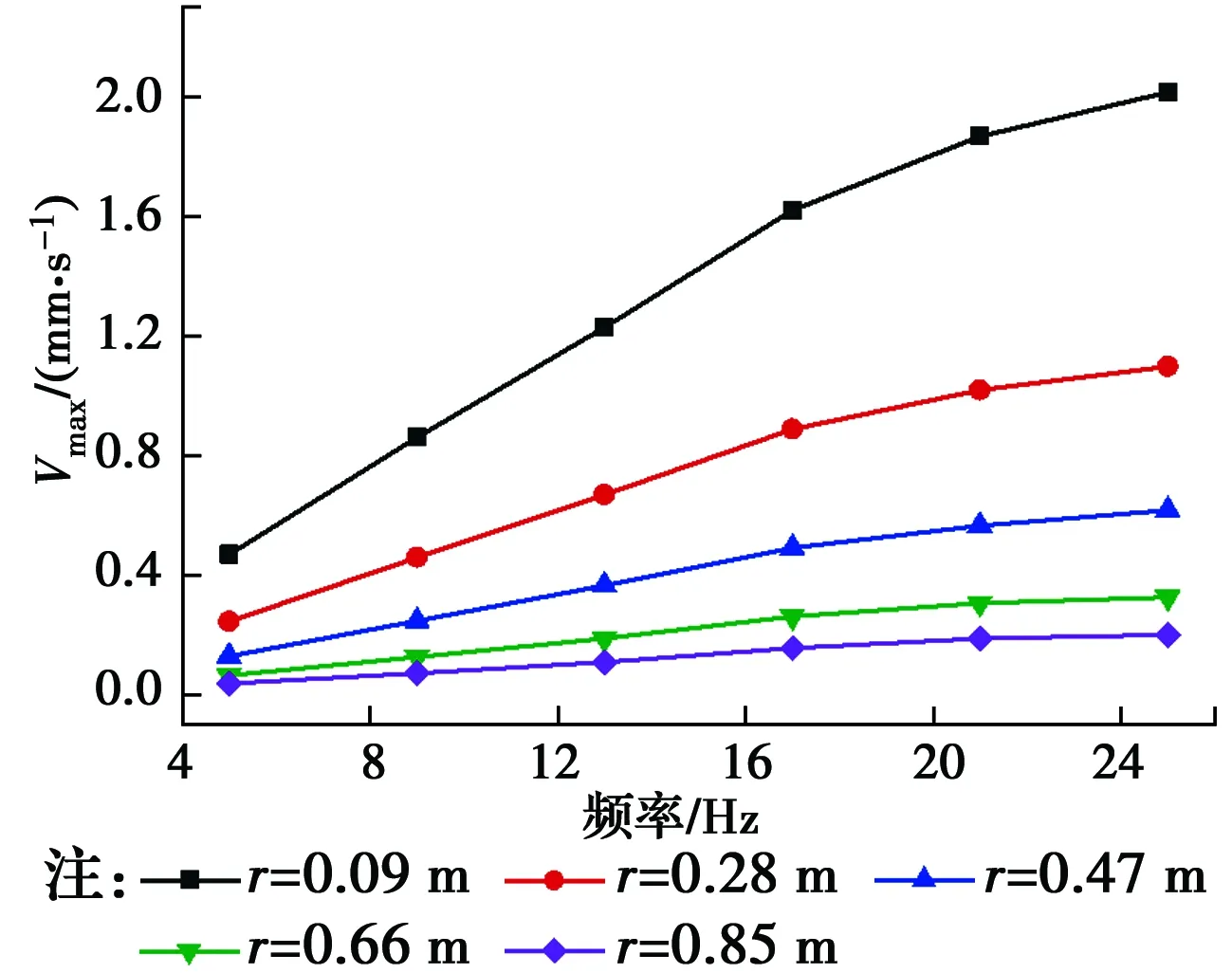
圖15 地面振動響應隨頻率變化規律Fig.15 Variation of ground dynamic response with

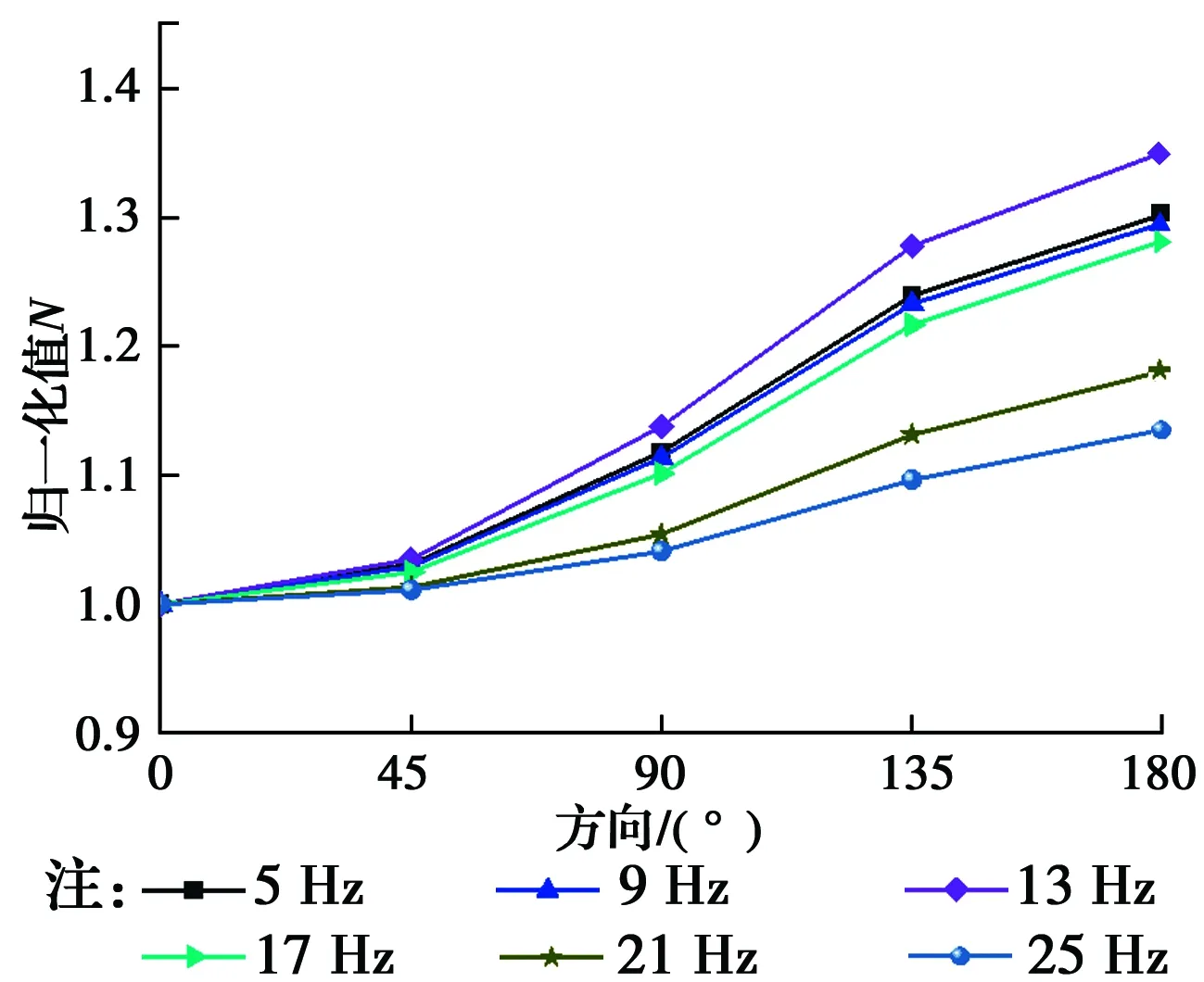
圖16 r=38 cm環線上速度響應隨頻率變化Fig.16 Variation of velocity response with frequency for the case of r=38

圖15表示地面距樁不同距離處速度峰值隨荷載頻率的變化規律。隨著荷載頻率增大，地面振動響應逐漸增大，且距樁越近速度峰值隨頻率增加越快，在距樁較遠處，隨荷載頻率增加地面振動響應變化不大。當荷載頻率在17 Hz以下時，振動速度峰值隨頻率呈線性增加；當頻率大于17 Hz時，地表響應速度峰值增速逐漸變緩。

圖16、圖17給出了與樁等距離圓上各方向振動響應差異隨頻率的變化規律。當頻率在13 Hz附近時，各方向的振動差異最為明顯，之后，隨著頻率增加各方向的差異性逐漸減小，在距離較遠處與樁同心圓上的各方向差異性顯著大于較近處的響應差異。值得注意的是，隨著頻率的增加，在距離樁較遠處與樁同心圓上振動響應最小值開始出現在45°方向上，即45°方向衰減速率開始變得最快。

3.3 樁長的影響

地面振動響應和與樁等距離各方向地表振動響應差異隨樁長L變化規律分別如圖18、圖19所示。

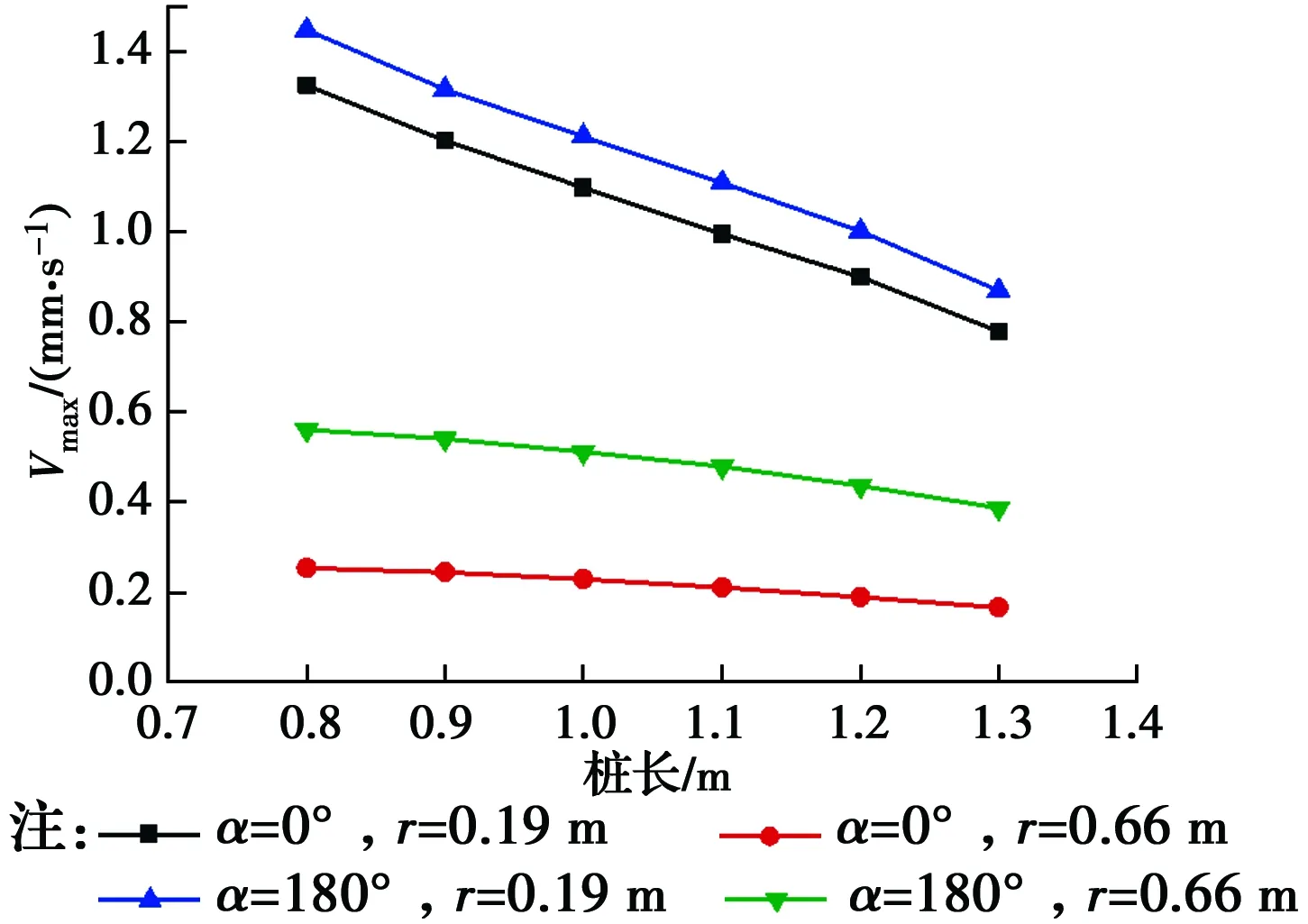
圖18 地面振動響應隨樁長變化規律Fig.18 Variation of ground vibration response with pile

從圖18可以看出，地表振動響應隨著樁長的增加呈線性減小，距樁較近處地表振動響應比遠處減小更快，且在等距離的0°和180°方向減小速率較為一致，距離較遠處0°和180°方向的速度峰值差異較大；圖19給出了與樁等距離處(r=68 cm)各方向振動響應差異隨樁長的變化規律。隨著樁長的增加，各方向的速度響應差異逐漸增大，但影響并不明顯；0°和45°的速度響應差異較小，從45°到180°方向速度響應差異開始急劇增大。

以上分析了基巖傾斜角度、荷載頻率、樁長等參數對地表振動衰減的影響。由分析可知，基巖傾斜角度越大或樁長越長時，地面振動響應越小。在實際工程設計中，可以考慮通過增加樁長和合理選擇地形位置來達到減小地面振動的效果。

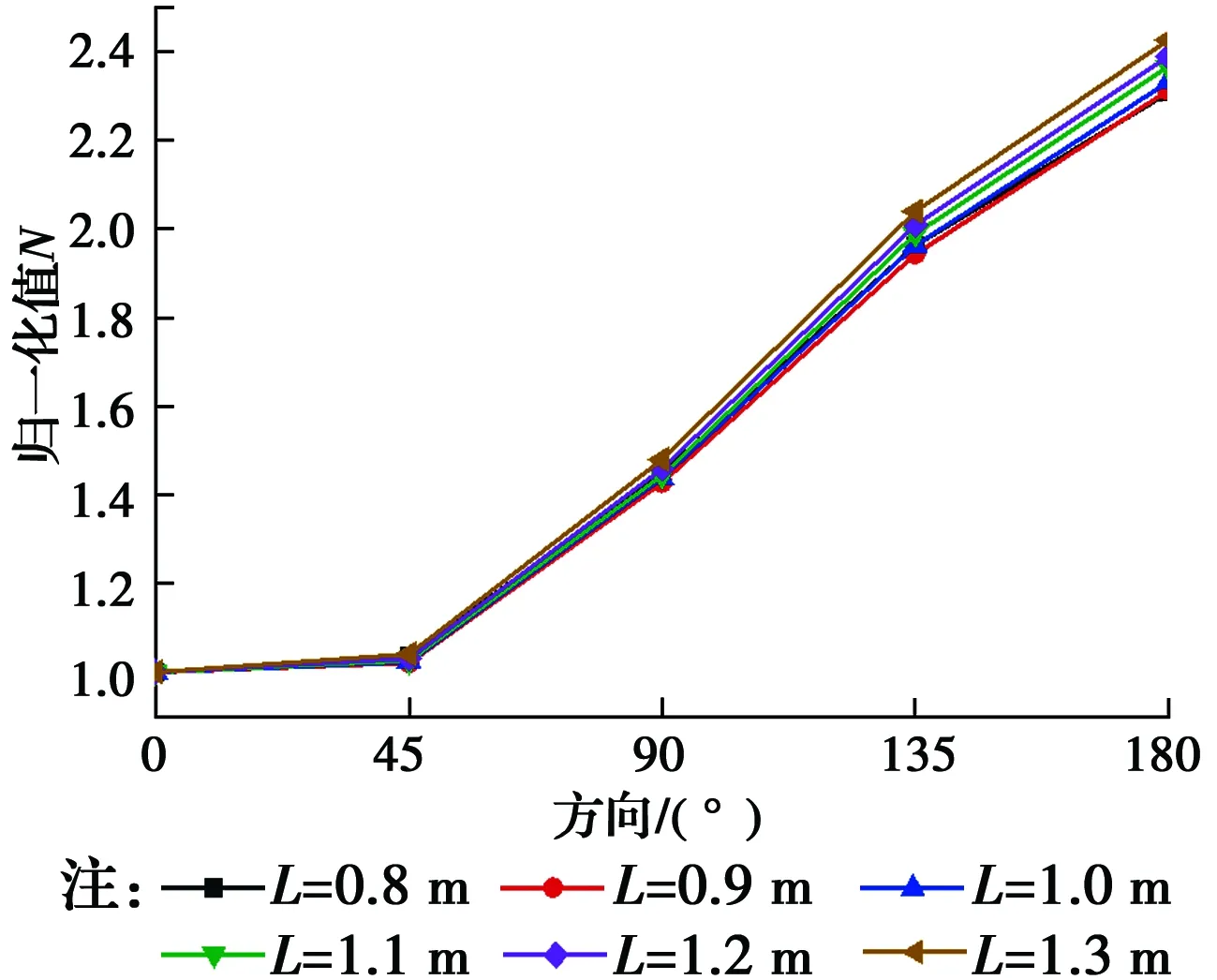
圖19 r=68 cm環線上速度響應隨樁長變化Fig.19 Variation of velocity response with pile length for the case of r=68

4 結論

通過模型槽試驗與數值模擬相結合的方法，分析了傾斜基巖層地形條件下軌道交通引起地表振動的衰減規律，可以得到以下結論：

1)傾斜基巖條件下，地表振動響應呈現出方向差異化，一般沿基巖正下方衰減最慢，沿基巖正上方衰減最快，并從正下方到正上方衰減逐漸變快。

2)在地表與樁同心圓上，各方向速度響應存在差異性，且距離越遠處差異性越大，從基巖正上方向到基巖下方向各點的速度響應峰值逐漸增大，但當基巖傾斜角度較小或荷載頻率較大時，在距離樁較遠處，同心圓上速度響應最小值會出現在與基巖正上方呈45°的方向上，這是受到頻率、樁長、基底傾斜角度等因素的影響所致。

3)基巖傾角越大，地面振動響應越小，傾角變化對地表振動衰減規律也呈現方向差異化影響，在基巖正上方向，地面振動衰減隨基巖傾角增大逐漸增快；在基巖正下方向，振動衰減規律不受角度變化影響。基巖傾角變化對與樁同心圓上各方向的振動響應差異化影響較為顯著。

4)隨著荷載頻率的增加，地表響應速度先呈線性增大，然后增速變緩。頻率對與樁等距離的圓上各方向速度響應差異性影響較為顯著，當荷載頻率為13 Hz時，各方向響應差異最大，然后隨著頻率增大，差異性逐漸減小。

5)地表速度響應隨樁長增加呈線性減小，且距樁越近，速度響應減小越快，樁長變化對與樁等距離圓上各方向速度響應差異化影響并不明顯。