例談數形結合在初中數學教學中的有效應用

張宏

摘 要：數和形是數學課程中緊密相關的兩個最基礎元素。數形結合思想方法中，教師主要利用板書、多媒體設備等，通過優化數形結合形式，將抽象的數學語言、數量關系與直觀的幾何圖形進行有機轉化，促使“數”與“形”相互對應、相互促進，實質上就是代數問題與幾何問題間的互相變換。

關鍵詞：初中數學;數形結合;教學應用

一、在初中數學教學中應用數形結合思想方法的意義

（一）有助于直觀呈現數學知識，優化形成數學概念

應用數形結合思想方法，能夠轉變數形呈現形式，讓枯燥的數學知識活躍起來，激發學生的興趣，調動起學生主動探求、理解和掌握數學知識的欲望;能夯實概念認知基礎，幫助學生從多視角認識抽象的數學概念，使學生熟練把握概念，深化理解概念。

（二）有助于增強學生的數學問題意識，激發數學思維活性

應用數形結合思想方法，能夠從不同的數學形式、不同的角度捕捉數學各要素的共性，引導學生將代數知識與幾何知識巧妙聯系起來，借助數形的多維轉換來思考問題，有利于增強學生的問題意識，激活學生的思維活性，提升學生的思維能力。

（三）有助于完善數學認知結構，提升解決問題能力

應用數形結合思想方法，有利于學生把握數學知識、概念、公理、定理、方法、內容之間的有機聯系，提高學生的知識遷移能力，形成良好的認知結構，進而提升自身解決數學問題的能力和素質。

二、數形結合思想方法在初中數學教學中的應用例析

（一）應用數形結合，優化形成數學概念

概念是學習數學的起點和基礎。初中生常接觸到許多數學概念，面對這些抽象的概念公式常感到不知所措，無法準確理解數學概念，對數學學習造成一定阻礙。

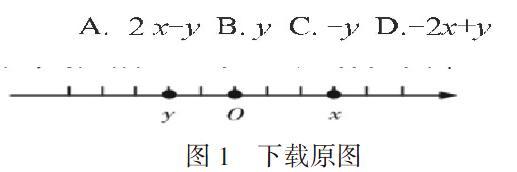
在初中數學教學中，教師可將一些直觀圖形或模型與相關數學概念整合在一起，對概念進行分析教學，從而使數學概念更形象化、簡單化，使學生更好地理解每個概念中對應的模型和方法，從而完整地把握數學概念。例1：如圖1所示，觀察實數在數軸上的位置，請化簡 ? ? ，并進行計算、選擇。

在這道題中，結合數軸，通過觀察得知x>0，y<0，從而判斷出x-y>0，進而化簡、合并，得出 ? ? ? ? ，應選C。

由此可見，通過觀察實數在數軸上的點的對應位置，理解并應用實數的相關概念和性質，能很直觀地獲取相反數、絕對值、距離等數量信息，進而更好地把握數軸這一特定幾何圖形的概念。

（二）應用數形結合，增強數學問題意識

為更好地激發學生的問題意識，教師可以借助優設課堂問題導入、創設課堂問題情境、營造和諧課堂氛圍等有效形式，激勵學生主動思考、敢于質疑。例如，在教學七年級上冊“有理數”一課時，就有學生產生了疑問：“什么是有理數？正負數概念與有理數概念有什么聯系嗎？如何理解掌握有理數的加法法則？”針對學生的問題，教師在黑板上繪制了一條數軸，并在數軸的中點標注上原點，引導學生沿著數軸上設定的正方向數了三個單位“1”，又向數軸的負方向數了兩個單位“1”，引導他們理解“3+（-2）”的含義，進而使他們順利得出“1”這一結果。

在此，教師借助“以形助數”的有效方式，通過復習數軸含義，滿足了學生的問題意識，使他們從數軸上點的移動方向和移動的距離清晰地梳理出數量表達式中蘊含的數學意義，明確了有理數的基本知識，提高了學習效率。

（三）應用數形結合，提升析題解疑能力

數學教學的精髓在于培養學生深度探索的學習精神，析題解疑能力是培養初中學生數學能力的根本。教師指引學生應用數形結合思想方法解決各種數學問題，能不斷提升他們分析題型、解決疑問的能力。

教師應用數形結合的思想方法，應結合各類定理的應用問題進行探索研究。例如，在八年級教學上冊“勾股定理”一課時，涉及“勾股定理”的作圖題：“在一個數軸上作出表示無理數的

點。”許多學生都能較好地在數軸上作出 ? ? 等簡單的無理數的點，但對于如何表示較為復雜的無理數，他們感到無從下手。此時教師應指導學生善用數形結合的思想方法，借助“以數造形、數形交融”方法，構造一個包含已知無理數的直角三角形，幫助學生成功解決問題。

師：我們一起探討如何在數軸上作出表示無理數 ?的點。由于13=9+4，此外還能以哪兩個正整數來相加減呢？

生：13=12+1，13=10+3，13=17-4……

師：非常好，也就是可變形

同學們想選擇哪個算式來構建直角三角形呢？

生：選

師：這是為什么？

生：因為這個算式最簡單，只需構建一個直角邊為2、3的直角三角形，且2、3都是正整數，很容易就得到長為 ?的邊。

師：很好。那接下來你們模仿上面的算式推演，嘗試在數軸上作出表示出 ?的點吧。

教師指引學生參與“以數造形、數形交融”訓練，構建一個恰當的直角三角形，再由“形”到“數”逐步呈現，使學生在經歷探索中明確了如何利用構建直角三角形來表示特定的無理數的點，有效克服了學生的思維盲點，使他們在探究學習的過程中深刻領會到數形結合思想方法在解題中的意義。

三、結語

教師應用數形結合的思想方法，幫助學生熟悉數與形之間的靈活轉換，深度理解代數和幾何的關系，能使學生有效地解決數學問題。教師應堅持結合課堂教學實際，優化數形結合的思想方法，指導學生訓練數形結合思維，提高學生靈活變通的學習能力，不斷提升其學習效果。

參考文獻：

[1]李巖青.初中數學教學中數形結合思想的實踐探析——以北師大版初中數學教材為例[J].數學學習與研究，2018，12（24）：56.

[2]陳長春.基于數形結合，構建高效數學課堂[J].數學教學通訊，2018，10（29）：78-79.