整體求解思想在初中數學中的應用
——以整式乘法與因式分解為例

陳迎建

整體求解方法基于整體求解思想是數學解題過程中的一種重要方法，在初中數學解題方法中占有重要的地位。整體求解思想的灌輸對初中生而言，不僅僅是數學問題的解決，更是思維的培養與鍛煉以及看待問題的角度的拓展。對于整體求解思想的定義往往因人而異，但總的來說可以歸納為：整體求解思想是初中數學教學思想的一種，其基于宏觀、整體的層面其看待，理解、分析問題，角度更加寬泛。

在初中數學的教學過程中，不斷滲透、灌輸整體求解思想，是數學改革的重要要求，也是教學重點與難點。讓學生在學習過程中不斷地去體會整體變換、相互代換以及事物之間存在的的普遍聯系，從而加深對數學的認識與理解。初中生處在直觀思維到邏輯思維的變化過程中，在數學的解題過程中將會受到思維定式、顧此失彼的影響，降低學生學習數學的熱情及積極性，整體思維的學習既能拓寬學生的思維，提高學習的興趣，又能幫助學生去整體、全面的把握、看待問題，培養鍛煉學生的創造性思維。學生能夠更加徹底的、明確的認識數學、了解數學，提高處理問題的能力與水平。

整式乘法與因式分解這一章蘊含著豐富的整體求解思想。完全平方公式以及利用完全平方公式進行因式分解練習中，學生需好好把握整體求解思想。如以下三個公式：

這里①、②可以說明兩項和（差）的平方等于兩項平方之和加上（減去）兩項的2倍。教學中可以以：首平方，尾平方，首尾二倍在中央，符號看前方去記憶和理解。公式③理解為兩項和乘兩項差等于兩項平方之差。在學習的過程中，學生應該理解”a”、“b”所代表的是一項，一個整體，而不能單純的看成一個字母、一個數字，一個單項式。特別在利用完全平方公式進行因式分解的過程中要特別注意。

筆者將通過以下四個常見的整體求解方法在乘法公式與因式分解這一章的應用進行闡述。

一、整體換元法的應用

整體換元法指的是在數學的解題過程中，設立一個新“元”即新的變量去表示或者代替條件中的已知式或者其中的某一部分，從而達到化煩為簡的目的，利于快速解題。

例1：已知（2000-a）（1998-a）=1999，那么（2000-a）2＋（1998-a）2=。

分析：條件及問題中皆出現了2000-a、1998-a這兩個代數式，因此可以把它們分別看成一個整體，利用整體換元的方法去解決。設2000-a=m，1998-a=n，將問題轉化為已知mn=1999，求m2＋n2的值.根據完全平方公式，還缺少m＋n或m-n的值，再根據隱含條件m-n=（2000-a）-（1998-a）=2就可以利用m2＋n2=（m-n）2＋2mn求解.

解答：設2000-a=m，1998-a=n，則mn=1999，m-n=2，

所以需要好好體會完全平方公式在應用過程中整體思想的把握理解，即把某一代數式看成一個整體作為公式的一項。

引申：已知（x-2015）2＋（x-2017）2=34，則（x-2016）2的值是（ ）

解題過程：

解：設x-2016=y則x-2015=y＋1，x-2017=y-1

∴ (y＋1)2＋(y-1)2=34 ∴y2=16

∴ (x-2016)2=16

例2：將 (x2-4x＋6) (x2-4x＋2) ＋4進行因式分解

分析：條件兩項多項式中均含有x2-4x，可以把它看成一個整體，利用整體換元法進行運算。

解題過程：解：設x2-4x=y

二、整體代換法的應用

在數學的求解過程中，特別是代數式求值中，題目所給的條件無法直接利用到問題中進行求解。可以根據所求問題的條件和結論，選擇條件或者問題的中的某一個或者幾個代數式作為一個整體，去觀察尋找問題與條件的關聯并進行靈活的變通，從而達到簡化求解的效果。

例1：已知x2＋x-5=0，則代數式（x-1）2-x（x-3）＋（x＋2）（x-2）的值為.

分析：條件問題無直接聯系，所以先利用乘法公式展開，原式=x2＋x-3.此時可以發現所求代數式與條件的聯系：將x2＋x=5整體代入可以較為容易的求出答案。

解題過程：原式=x2-2x＋1-x2＋3x＋x2-4=x2＋x-3

∵x2＋x-5=0 ∴x2＋x=5 ∴原式=5-3=2

例2：a2-3b=4，則6b-2a2＋2019=______

分析：觀察問題中6b-2a2與條件存在-2倍的關系，及6b-2a2=-2（a2-3b）。將a2-3b=4整體代入進行求解。

解題過程：∵6b-2a2＋2019=-2(a2-3b) ＋2019

又∵a2-3b=4 ∵原式=-2x4＋2019=2011

三、整體變形法的應用

在本章的學習過程中，要理解字母“a”、“b”所代表的是一個項，一個代數式。在練習過程中，有意識的將題目中的部分作為一個整體進行處理，從而使得問題呈現出一定的規律或者熟知的的公式定理，達到簡化計算過程，減少運算量的效果。

例1：計算（a＋2b-3c）（a-2b-3c）.

分析：從題目來看與所學的平方差公式地形式相仿，但又有不同之處。平方差公式是兩項和乘兩項差，因此需要將題目中的某兩項看成一個整體，從而利用公式進行求解。

在找平方差公式中的“a”與“b”需要注意，對于此類題型，只要將各括號內的符號相同項看成一個整體，作為公式中的“a”，再將符號相反項作為一個整體，看作公式中的“b”，就可以利用平方差公式進行求解。

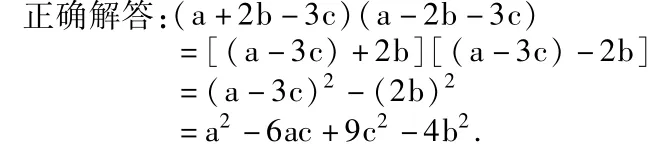
例2：因式分解：（a2-4a）2＋8（a2-4a）＋16

分析：根據條件，其符合完全平方公式的基本特征。利用完全平方公式去進行因式分解，學生需理解a2-4a作為一個整體項，也就是公式里的“a”。

四、整體配方法的應用

在數的練習過程中，利用整體配方法也是解決問題的一種常用方式。就目前學習而言，學生需要對完全平方公式地有一個徹底的認識。能夠根據已給的條件中，進行適當的拼湊，使之滿足完全平方公式的基本結構，從而達到簡化問題，減少計算，簡化答題的目的。

例1：若a2＋b2＋4a-2b＋5=0，求a、b的值。

分析：條件出現a2＋4a，那么根據完全平方式的基本結構，a2作為首平方，4a作為首尾項的2倍，可得出尾項平方為22即整體配方為(a＋2)2，同理得b2-2b可配方為(b-1)2。解析過程：

∵ a2＋4a＋4＋b2-2b＋1=0 ∴ (a＋2)2＋(b-1)2=0

∵ (a＋2)2≥0且(b-1)2≥0 ∴a＋2=0，a=-2 b-1=0，b=1

延伸：若4a2＋b2＋c2-2ab-3b＋6c＋12=0，求a＋b＋c的值

分析：從條件來看，出現了c2＋6c，根據整體配方需要在加上32構造成完全平方公式。同理，由4a2-2ab兩項，需要再加上一項整體構造。解題過程如下：

例2：已知a，b是一個等腰三角形的兩邊長，且滿足a2＋b2-4a-6a＋13=0，求這個等腰三角形的周長。

分析：根據a2-4a整體構造完全平方公式需要加上另一項22，同理b2-6b需要加上第三項32。解題過程如下：

解：∵a2＋b2-4a-6b＋13=0

∴（a2-4a＋4）＋（b2-6b＋9）=0

∴（a-2）2＋（b-3）2=0 ∴a=2，b=3

所以當腰長為2時，等腰三角形的周長是2＋2＋3=7；當腰長為3時，等腰三角形的周長為2＋3＋3=8；綜上，該等腰三角形的周長是7或8

總結：整體求解思想是初中數學主要的解題思想之一，在數學學習過程中占有重要的地位。在整式乘法與因式分解這一章中，整體求解思想有著充分地體現。整體換元方法、整體代換法、整體變形法、整體配方法在本章節有著重要的應用，是解決乘法公式及因式分解的重要方法。整體求解思想的貫徹與理解，不僅提高學生解決問題的能力，而且有助于學生的創造性思維及邏輯思維的培養，對于學生的發展有著重要地意義。