精心設(shè)計，優(yōu)化整合
——以一元一次不等式（組）復(fù)習(xí)為例

☉浙江省桐廬縣實(shí)驗(yàn)初級中學(xué) 王良弟

在八年級數(shù)學(xué)復(fù)習(xí)階段，為了讓學(xué)生將知識系統(tǒng)化、明朗化，在期末考試中旗開得勝，筆者做了幾個復(fù)習(xí)專題課.一方面，筆者整理了常考的知識點(diǎn)，另一方面，筆者認(rèn)真分析了2018年一些地市的中考試題，從中分析了中考的考向和一些解題策略，編寫進(jìn)專題導(dǎo)學(xué)案中讓學(xué)生再認(rèn)知、再探究、再運(yùn)用.

一、鎖定目標(biāo)，為學(xué)生明確復(fù)習(xí)方向

筆者深知復(fù)習(xí)過程不是簡單的知識重復(fù)，而應(yīng)該是知識的梳理、整合與應(yīng)用.于是再次翻開課程標(biāo)準(zhǔn)，同時從網(wǎng)上查閱了近年來一些地市的中考試題，開卷有益.

在課程標(biāo)準(zhǔn)中，不等式內(nèi)容的主要思想是進(jìn)行數(shù)學(xué)建模，通過生活中的實(shí)際問題去培養(yǎng)學(xué)生學(xué)會質(zhì)疑、解疑的能力，從而讓學(xué)生認(rèn)識到不等關(guān)系在生活中是一種重要的數(shù)量關(guān)系，其性質(zhì)和解不等式（組）是數(shù)學(xué)的基本運(yùn)算技能，也為今后進(jìn)一步學(xué)習(xí)函數(shù)、方程和不等式打下堅實(shí)的基礎(chǔ).因此，在一元一次不等式（組）的復(fù)習(xí)專題中，必須把精準(zhǔn)構(gòu)建一元一次不等式（組）的解法和應(yīng)用所學(xué)知識解決一些實(shí)際問題作為知識目標(biāo)；將幫助學(xué)生認(rèn)識建模思想和化歸思想，在合作交流中內(nèi)化分析能力、推理能力和解決問題能力，在解題探究中形成創(chuàng)新意識作為能力目標(biāo)；將在積極參與、各抒己見中養(yǎng)成嚴(yán)謹(jǐn)?shù)膶W(xué)習(xí)態(tài)度，提升探究問題的意識，提升思維的敏捷性，從而激發(fā)數(shù)學(xué)學(xué)習(xí)的欲望，增強(qiáng)在期末考試中對數(shù)學(xué)學(xué)科的信心作為情感目標(biāo).

二、梳理知識，為學(xué)生做好解疑鋪墊

梳理知識時可以將課本上一元一次不等式（組）的知識點(diǎn)進(jìn)行歸類，讓學(xué)生明確每個知識點(diǎn)的應(yīng)用范圍及它們之間的內(nèi)在聯(lián)系；能幫助學(xué)生準(zhǔn)確把握一元一次不等式（組）內(nèi)容的重點(diǎn)、難點(diǎn)，加深對各個知識點(diǎn)的理解和應(yīng)用；特別是在做完相應(yīng)知識點(diǎn)的訓(xùn)練后讓學(xué)生學(xué)會歸納這個題所應(yīng)用的知識點(diǎn)，便于在期終考試中遇到類似題時，能夠沉著冷靜，快速判斷出解決這個問題應(yīng)該應(yīng)用的知識點(diǎn).

在導(dǎo)學(xué)案編寫時，筆者是這樣梳理知識的.

知識點(diǎn)1：一元一次不等式（組）的概念.

用相關(guān)的數(shù)學(xué)語言，如“＞”“＜”“≠”“≤”等符號連接的式子稱為不等式，含兩個以上不等式的稱為不等式組.在應(yīng)用中還用到一些關(guān)鍵詞，如“超過（不超過）”“多于（不多于）”“低于（不低于）”“至少（至多）”等.

對點(diǎn)練習(xí)1：讓學(xué)生用不等式表示下列敘述的文字.

（1）x的4倍減去10大于2，x的2倍加上10小于2；

（3）a是不超過100的非負(fù)數(shù).

創(chuàng)設(shè)目的：首先讓學(xué)生理解不等式的基本概念，然后進(jìn)行針對概念的練習(xí)，這些一元一次不等式（組）是建立在不等式的基礎(chǔ)上的，尤其是第（3）小題，看似簡單，卻蘊(yùn)含大世界，學(xué)生誤認(rèn)為“不超過”是“＜”而忽視“=”，將“非負(fù)數(shù)”錯誤解讀成“＞0”，沒有理解“0”也是非負(fù)數(shù).讓簡單易錯的練習(xí)為學(xué)生今后的解題敲響警鐘，這是設(shè)計練習(xí)的關(guān)鍵所在.

知識點(diǎn)2：關(guān)于不等式的基本性質(zhì).

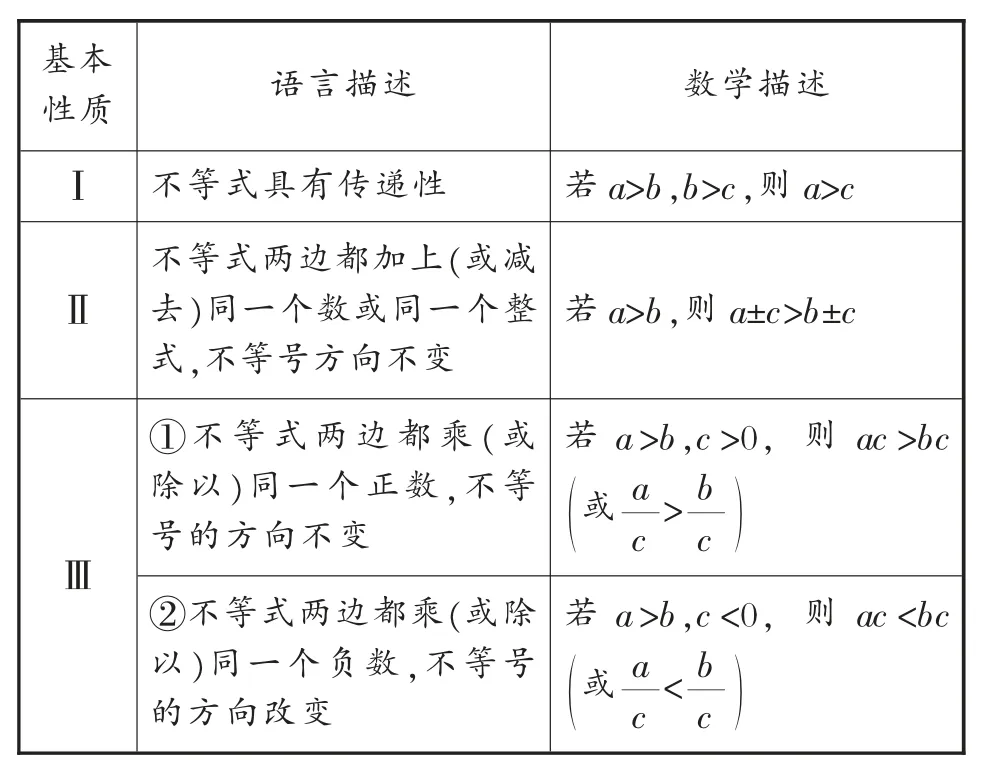
表1

對點(diǎn)練習(xí)2：用不等號填空：

（1）若ax≤by，則-ax+10______-by+10；

（3）若q＜r，則qx_______rx.

創(chuàng)設(shè)目的：在學(xué)生對不等式的基本性質(zhì)的再次認(rèn)知后進(jìn)行針對不等式性質(zhì)的練習(xí)，有利于學(xué)生對不等式的性質(zhì)的理解與鞏固.第（1）小題的設(shè)置，檢測學(xué)生對不等式性質(zhì)Ⅱ和Ⅲ②的認(rèn)知；第（2）小題的設(shè)置，檢測學(xué)生對不等式性質(zhì)Ⅰ和Ⅲ②熟練掌握的程度，某些學(xué)生僅僅會將不等式兩邊乘以之后，得出m＜-6，而后“卡殼”；第（3）小題的設(shè)置，檢測學(xué)生對不等式性質(zhì)Ⅲ①和Ⅲ②的理解，學(xué)生僅僅作出x＞0和x＜0的討論，而忽略x=0，讓答案不完整.因此，在復(fù)習(xí)備考時，一方面，要注意基礎(chǔ)，另一方面，還要考慮不等式性質(zhì)的綜合應(yīng)用.

知識點(diǎn)3：關(guān)于不等式的解法.

（1）不等式的解集.

描述什么是不等式的解的集合（即不等式的解集）.

（2）什么是解不等式？不等式的解集有哪些表示方法？

在課堂上強(qiáng)調(diào)不等式的解集的兩種表示方法，即用不等式表示，或用數(shù)軸表示：大于開口向右，小于開口向左，有等號的畫實(shí)心圓點(diǎn)，無等號的畫空心圓圈（應(yīng)用于一元一次不等式組更為方便）.

（3）常見的解一元一次不等式的步驟.

去分母（同解一元一次方程）→去括號（不等式的基本性質(zhì)Ⅲ）→移項(xiàng)（不等式的基本性質(zhì)Ⅱ）→合并同類項(xiàng)→系數(shù)化成1（不等式基本性質(zhì)Ⅲ）.

對點(diǎn)練習(xí)3：求下列不等式的解，并在數(shù)軸上將解表示出來：

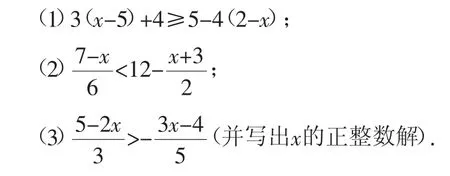
創(chuàng)設(shè)目的：在理解不等式的基本性質(zhì)的基礎(chǔ)上進(jìn)行練習(xí)，有利于學(xué)生對不等式的解法的理解與鞏固.給出的三個練習(xí)步步遞進(jìn)，第（3）小題要求寫出x的正整數(shù)解，也是為不等式在生活中的應(yīng)用奠定基礎(chǔ).

知識點(diǎn)4：一元一次不等式組的應(yīng)用.

一元一次不等式組的應(yīng)用這部分知識與解不等式是不可分割的，學(xué)會求解一元一次不等式也就輕松解決一元一次不等式組的求解了.但其應(yīng)用則有著更深的內(nèi)涵，需要學(xué)生在生活背景的練習(xí)中去體會.

對點(diǎn)練習(xí)4：（1）若是關(guān)于x、y的二元一次方程組，其中x-y＜2，求實(shí)數(shù)m的取值范圍.

（2）圖1是關(guān)于x的不等式m-2x≥1的解集，那么，m的取值是_________.

圖1

（3）隨著生活質(zhì)量的提高，越來越多的居民選購家用電餅鐺.某小電器商場抓住機(jī)遇，從廠家購進(jìn)了1-01、1-02、1-03三種型號電餅鐺共x臺，1-01型號電餅鐺進(jìn)價是120元/臺，1-02型號電餅鐺進(jìn)價是160元/臺，1-03型號電餅鐺進(jìn)價是280元/臺.

①若x=200，購進(jìn)兩種型號的電餅鐺共用去18000元，求1-01、1-02、1-03三種型號電餅鐺各購進(jìn)了多少臺.

②為使每臺1-02型號電餅鐺的毛利潤是1-01型號的2倍，每臺1-03型號電餅鐺的毛利潤與1-01型號相等，且保證售完這200臺電餅鐺的毛利潤不低于10000元，求每臺1-01型號電餅鐺的售價至少是多少元（注：毛利潤=售價-進(jìn)價）.

③若商家購買的總費(fèi)用為50000元，求x的最大值.

創(chuàng)設(shè)目的：小題（1）和（2）仍然采用數(shù)學(xué)的基本形式作為載體，旨在對數(shù)學(xué)問題的逐步深化，是讓學(xué)生回歸舊知、內(nèi)化吸收的過程，而小題（3）則是生活中一種應(yīng)用性的練習(xí)，有利于學(xué)生在練習(xí)中獲取生活經(jīng)驗(yàn)，同時讓學(xué)生感悟到一元一次不等式組在生活中的應(yīng)用比比皆是.因此，學(xué)好這部分?jǐn)?shù)學(xué)知識是學(xué)生對生活熱愛的追求，也是利用數(shù)學(xué)建模來提升學(xué)科素養(yǎng)的良好載體.

總而言之，八年級學(xué)習(xí)過程是一個關(guān)鍵階段，期末考試備考復(fù)習(xí)可以有效提升學(xué)科成績.此時數(shù)學(xué)知識的難度明顯加大，學(xué)生往往顧此失彼，加強(qiáng)學(xué)法指導(dǎo)和增強(qiáng)備考意識是不容忽視的環(huán)節(jié).所以，唯有鎖定目標(biāo)，為學(xué)生明確復(fù)習(xí)方向；梳理知識，為學(xué)生做好解疑鋪墊，才能讓學(xué)生在期末考試中胸有成竹.