對新定義考題的解題研究與教學思考
——以南通2019年中考卷第28題為例
☉江蘇省海安市城南實驗中學 朱月鳳
新定義考題是近年來不少地區命題熱點,這類問題往往從一個定義出發,通過增設強化條件,組合成復雜的綜合難題,解題時需要深入解讀新定義、深刻理解新定義,并靈活運用.本文以2019年江蘇南通中考新定義壓軸題為例,解析思路并跟進教學建議,供研討.
一、新定義考題及思路突破
考題:定義:點(x,y),若x、y滿足x2=2y+t,y2=2x+t,且
x≠y,t為常數,則稱點M為“線點”,例如:點(0,-2)和(-2,0)是“線點”.
已知:在直角坐標系xOy中,點P(m,n).
(1)P1(3,1)和P2(-3,1)兩點中,點______是“線點”.
(2)若點P是“線點”,用含t的代數式表示mn,并求t的取值范圍.
(3)若點Q(n,m)是“線點”,直線PQ分別交x軸、y軸于點A、B,當|∠POQ-∠AOB|=30°時,直接寫出t的值.
思路突破:(1)直接代入定義中提到的兩個等式運算后可確認點P2是“線點”.
(2)提供兩種思路.
思路1:由“線點”定義可得:
m2=2n+t ①,
n2=2m+t ②.
①-②,得(m+n)(m-n)=2(n-m).因為m≠n,所以m+n=-2.
①+②,得m2+n2=2(m+n)+2t,配方得(m+n)2-2mn=2(m+n)+2t.
把m+n=-2代入,得4-2mn=-4+2t,整理得mn=4-t.
由m+n=-2,得點P(m,-m-2).代入x2=2y+t,有m2=2(-m-2)+t,整理得t=m2+2m+4=(m+1)2+3.
當m=-1時,n=-1,這里m=n,不舍題意,舍去.
當m≠-1時,都有t>3.
綜上,t>3.
思路2:由m+n=-2,得點P(m,-m-2).代入x2=2y+t,有m2=2(-m-2)+t,整理成關于m的一元二次方程m2+2m+4-t=0.
由該方程有實數根,得Δ=4-4(4-t)=4t-12≥0,解得t≥3.
當t=3時,解得m=-1,此時m、n相等,故t≠3.
綜上,t>3.
思路3:由點P(m,n)是“線點”,得m2=2n+t,n2=2m+t,則m2-n2=2(n-m),m2+n2=2(n+m)+2t.又m≠n,則m+n=-2.(n+m)2-2mn=2(n+m)+2t,則4-2mn=-4+2t,則mn=-t+4.由m≠n,得(m-n)2>0,即(n+m)2-4mn>0,則t-3>0,解得t>3.則t的取值范圍為:t>3.
(3)先初步解讀條件,由于點P(m,n)、Q(n,m)也為線點,所以點P、Q在直線y=-x-2上且關于直線y=x對稱(如圖1),結合|∠POQ-∠AOB |=90°,可 得∠POQ=60°或∠POQ=120°.
以下提供三種思路進一步分析.
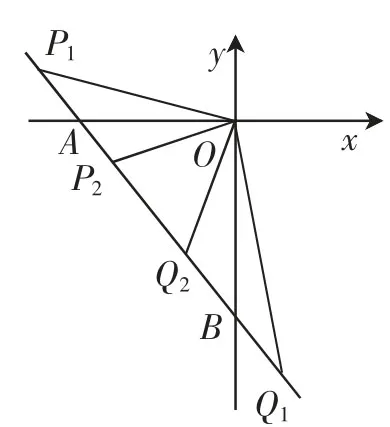
圖1
思路1:分兩種情形討論120°或60°的情形.
①若∠P1OQ1=120°,先求得P1O=.由點P1(m,-m-2),得m2+4+4m+m2=8,即m2+2m-2=0.即2-2m=2(-2-m)+t,解得t=6.
②若∠P2OQ2=60°,先求得P2O=.由點P2(m,-m-2),得m2+4+4m+m2=,即=0.即=2(-2-m)+t,解得t=
思路2:①若∠P2OQ2=60°,易知△P2OQ2為正三角形,可求出點又點Q2的坐標滿足x2=2y+t,代入后解得t=
②若∠P1OQ1=120°,△POQ為等腰三角形,分析出點.又點Q1的坐標滿足x2=2y+t,代入后解得t=6.
思路3:(基于高中圓的方程的視角)由點P(m,n)、Q(n,m)也為“線點”,得點P、Q在以O為圓心、r=的圓上.由|∠POQ-∠AOB|=90°,得∠POQ=60°或∠POQ=120°.
②當∠POQ=120°時,半徑OP=2(-x-2)=6.
二、解后反思與教學建議
這道新定義考題表述簡潔,閱讀量不大,但思維量大,解題教學時要辨明解題難點、關鍵步驟,然后預設必要的鋪墊帶領學生攻克難點.
先說第(2)問.這一問的難點或關鍵步驟有三處.第一處關鍵步驟是通過數式方程的變形求解分析出m、n之間的數量關系m+n=-2,這不僅對這一問的求解非常關鍵,而且對于下一問的探究十分重要,因為這個數量關系揭示了所謂“線點”P所在直線的方程.第二處關鍵是消去參數,將t用含有m或n的式子表示出來,借用方程或函數觀點進行最值分析.第三處關鍵在于t=3要舍去,只能取t>3,這是一個易錯點,因為需要對條件m、n不可能相等再次使用.想清辨明上述關鍵步驟,有助于教學時在這些關鍵步驟上預設一些鋪墊問題,幫助學生順利解答.
再說第(3)問.這小問的關鍵步驟至少有四處.第一處關鍵步驟是想清點P、Q都是“線點”,且它們關于直線y=x對稱,這是引導學生初步感受P、Q兩點位置的關鍵,如果這一點都沒有辨明,則起點不清,難以構圖.若學生沒有發現它們都是線點,教學時要引導學生:“有人說點P、Q都是線點,你同意他的說法嗎?”第二處關鍵步驟是確認“線點”P、Q在直線y=-x-2上,這是由上一問中提出的m+n=-2成果擴大而來的,這樣就可以將點P、Q的位置關系想清,然后結合角度關系式,就能精準定位點P、Q的位置了.第三處關鍵步驟是需要分類討論∠POQ為60°或120°的情況.不少考生容易漏解,對絕對值符號表示的關系式思考不深.第四處關鍵步驟是計算能力要過關.因為涉及15°角的邊角關系,需要構造圖形,轉化為含30°角的三角形進行分析求解.
三、關于新定義考題的解題研究與教學思考
近幾年各地新定義考題成為一個熱點題型,開展相關解題研究十分必要,同時針對新定義考題的教學研究也值得深入思考.
1.明辨新定義的本質或結構是解題關鍵
新定義考題往往是結合初中階段原有的一些定義或性質進行整合、包裝而成,這時需要明辨新定義的本質或對應圖形的本質特征,然后靈活運用新定義進行解題.解決這類問題的難點在于理解新定義,并靈活運用.因為數學教學過程中,關鍵就是帶領學生新學一類數學概念,學生往往對舊知或舊概念有較強的依賴,難以適應新的概念.根據教學經驗,進入初中新學方程之后,有些學生仍然會依賴小學階段的算術解法;全等三角形學習后期會引出角平分線的性質定理,但學生往往不能簡化運用,所以在新定義解題研究時,往往會出現這類思維障礙.
2.新定義考題往往需要精準構圖分析
新定義之后隨著解題條件的增設,往往需要考生繼續構造圖形分析,而很多考生往往是圖形構造不出來,或者圖形構造不準,影響思路獲得.像上文中的新定義考題一樣,有些考生并沒有分析出“線點”所在直線的方程或兩個“線點”關于直線y=x對稱,這樣構造圖形不成功,思路也就難以打開.再比如,北京地區的很多新定義考題,往往都與一些軌跡圓有關,而且有時還會出現“大小同心圓”的情況,如果這些“同心圓”不及時準確分析出來,當然不利于思路獲得.
3.新定義考題教學時要預設鋪墊問題
新定義考題多有一些關鍵步驟或易錯點,這就要求我們在開展新定義考題解題教學之前要認真研判、明辨關鍵步驟,基于班級學情想清學生的易錯點,然后針對這些易錯點、關鍵步驟進行鋪墊式設問,設計這些鋪墊問題不只是幫助學生順利解決一道新定義題,更重要的是通過鋪墊式問題,讓學生學會在以后獨立面對一些較難問題時,知道從哪些地方入手思考,如何發現較難題的解題思路或念頭,如何利用條件或定義揭示的結構組合在一起獲得進展,怎樣防范易錯點,如何審校答案的嚴謹與規范,等等.也就是通過解題教學讓學生學會思考(想得更合理、更高效).

