在解題中提高,在提高中升華*
——以幾何問題為例
☉江蘇省南京師范大學蘇州實驗學校 施文軍
一、問題現狀
眾所周知,幾何是初中數學重點學習的內容.在歷年各地的中考命題中有近50%的考題與幾何相關.由此可見,其重要性毋庸置疑.在多年的教學中,學生普遍認為初中幾何知識過于復雜,涉及的內容太多,考題變化多種多樣,面對一道題時,不知如何作輔助線,找不到解題的切入點.
二、考查要點
結合筆者多年教學經驗,發現在初一的時候我們幾乎已經把初中幾何所考的內容都學完了.面對這個問題,可能部分學生表示不認同.那么筆者的依據是什么?
實際上我們小學就學過幾何,只不過那時我們學習的重點是幾何圖形的基本性質,如周長、面積等.到了初中,除了豐富幾何基本性質,學習的重點則變成了在同一平面內幾何圖形的關系.但這些關系總的來說只有兩種:
(1)邊(線段)的關系,包括位置關系與數量關系.位置關系在初一的時候就學過了,只有垂直與平行兩種.不僅初中,甚至高中也只有這兩個關系會在考試中出現.邊的數量關系考點也只有三種:相等,比例,以及利用數量關系求線段長.
(2)角的關系,只有數量關系及利用數量關系求角度這兩種.
我們整整三年的初中數學,幾何只考這幾類問題.如下面兩例及其解析過程.
例1如圖1,在?ABCD中,∠BAD的平分線交BC于點E,交DC的延長線于點F,連接DE.
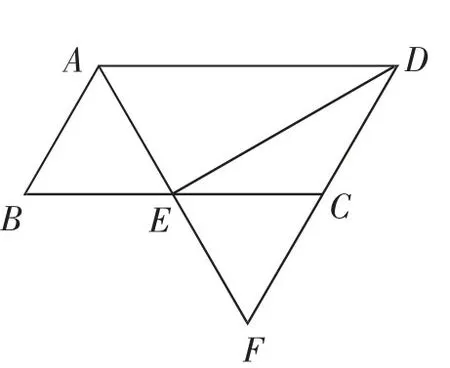
圖1
(1)求證:DA=DF;
分析:本題第(1)問證明兩條邊相等,即兩條線段的數量關系;第(2)問,求平行四邊形的面積,其實是尋找線段的數量關系.第(1)問的解答借助已知中的平行關系,從角的關系入手.第(2)問,通過挖掘題目中隱含的垂直關系,利用直角三角形中的三角函數和勾股定理來尋找邊的數量關系.(具體過程略)
例2如圖2,AB是⊙O的直徑,PA、PC與⊙O分別相切于點A、C,連接AC、BC、OP,AC與OP相交于點D.
(1)求證:∠B+∠CPO=90°;
分析:本題第(1)問考查的是角的數量關系,可從如下兩種視角求解.
方法1:由已知條件可得PO⊥AC.
因為PA、PC與⊙O分別相切于點A、C,所以OA⊥PA,PC=PA,∠PAC=∠PCA.∠CPO+∠PCA=90°.
因為AB是圓O的直徑,所以∠ACB=90°,所以∠B+∠CAB=90°.而∠CAB+∠PAC=90°,所以∠B=∠PAC.
綜上得∠B+∠CPO=90°.
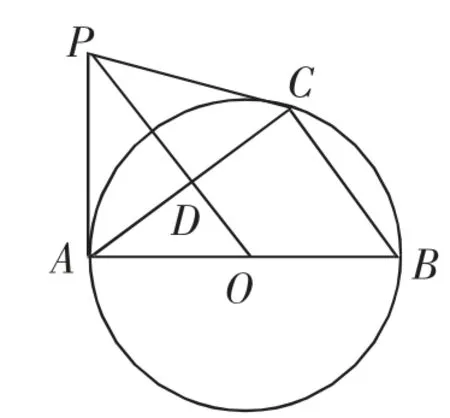
圖2
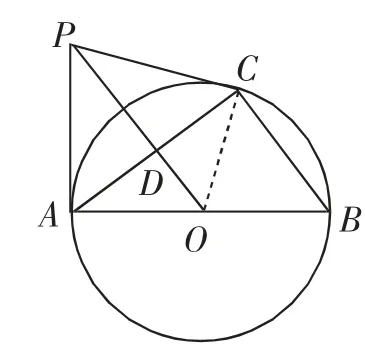
圖3
方法2:連接OC,如圖3.
因為PA、PC與⊙O分別相切于點A、C,所以OC⊥PC,OA⊥PA,∠APC=2∠CPO.所以∠OCP=∠OAP=90°.
因為∠AOC+∠APC+∠OCP+∠OAP=360°,所以∠AOC+∠APC=180°.又因為∠AOC=2∠B,所以∠B+∠CPO=90°.
第(2)問求邊的長度,可將其置于直角三角形中,利用三角函數及勾股定理求解.
如圖4所示,因為AB是⊙O的直徑,所以∠ACB=90°,∠ABC+∠BAC=90°.
因為∠ABC+∠CPO=90°,所以∠BAC=∠CPO=∠APO.

圖4
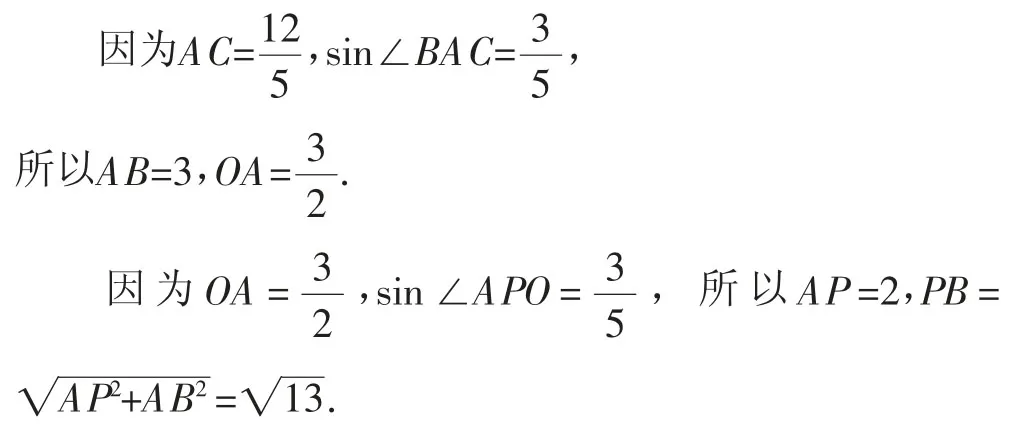
三、策略探析
以線段相等為例,初一我們學習的方法是利用三角形全等來證明線段相等,初二補充了利用特殊圖形(等腰三角形、平行四邊形、構造輔助圖形等)證明線段相等,初三學習函數之后又加入了解析法求線段長、證明線段相等.換句話說,我們所學的問題三年來并沒有增加,一直都是這幾類,而解題的思想方法每年都在增多.如:
例3 如圖5,在Rt△ABD中,∠BAD為直角,AC⊥BD于點C,CD=CE,BF⊥AE的延長線于點F.
求證:AC=CF.
分析:結合已知條件中所給的垂直關系,構造輔助圓,可簡潔證明.
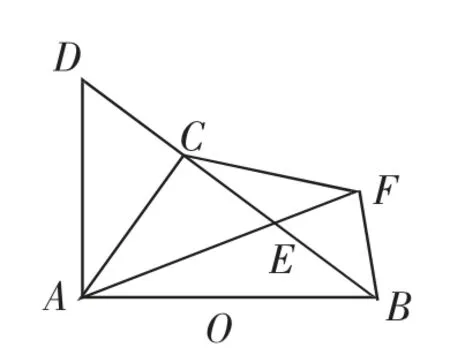
圖5
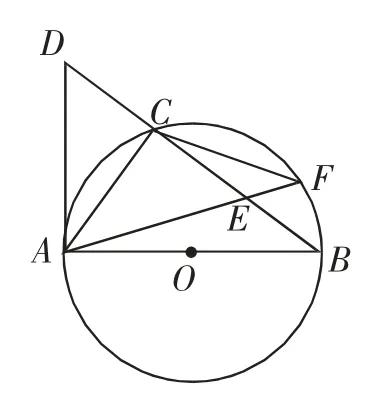
圖6
證明:以AB的中點O為圓心、AB為直徑構造圓,如圖6所示.
可得∠CAD+∠CAB=90°,∠ACB=90°,∠CAB+∠B=90°,則∠CAD=∠B.
因為CE=CD,所以AE=AD,∠CAE=∠CAD=∠B.又因為∠B=∠F,所以∠CAE=∠F.
所以AC=CF.
例4如圖7,AB是⊙O的直徑,弦CD⊥AB于點E,在⊙O的切線CM上取一點P,使得∠CPB=∠COA.
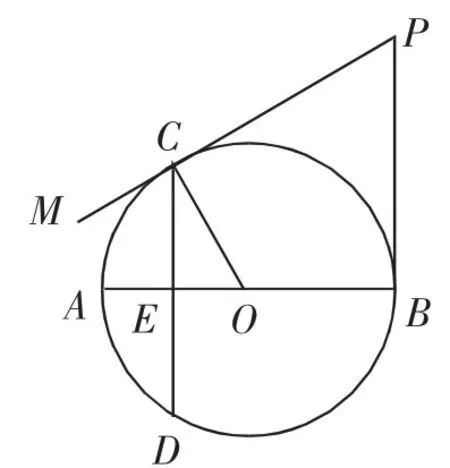
圖7
(1)求證:PB是⊙O的切線;
分析:第(1)問,求證PB是⊙O的切線,可從尋找線段的位置關系入手.
證明:因為PC與⊙O相切于點C,所以OC⊥PC,∠OCP=90°.因為∠AOC=∠CPB,∠AOC+∠BOC=180°,所以∠BOC+∠CPB=180°.
證明:在四邊形PBOC中,∠PBO=360°-∠CPB-∠BOC-∠PCO=90°,所以半徑OB⊥PB,即PB是⊙O的切線.
分析:第(2)問求邊的長度,既可以從邊的關系入手,也可從角的關系入手.
方法1:連接OP,如圖8.
因為PB、PC都是⊙O的切線,所以∠CPO=∠BPO,∠OCP=∠OBP,∠COP=∠BOP=60°.所以PB=OB·tan60°=6.
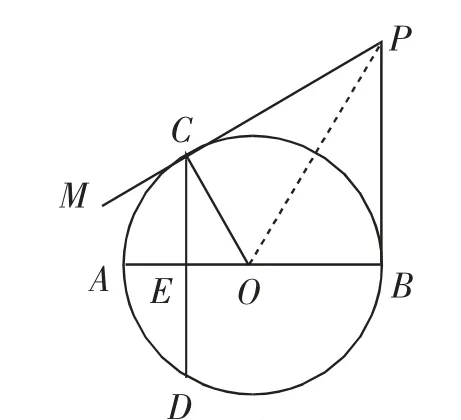
圖8
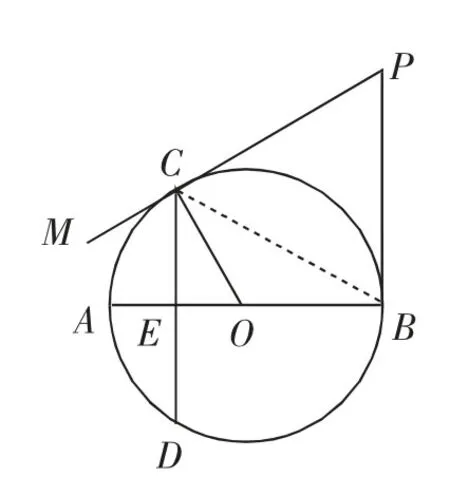
圖9
方法2:連接BC,如圖9.
因為PB、PC都是⊙O的切線,所以PB=PC.
所以△PBC為等邊三角形,所以PB=BC=6.
四、教學建議
筆者在教學中研究發現,大部分學生幾何成績不理想不是單純的基礎知識不好,而是不知道該從什么地方入手,不知道如何作輔助線.幾何題的難點在于圖形的變化和已知條件的隱蔽,問題往往都問得非常直接,這就可以成為我們的入手點.題中會明確告訴我們要求的是線段長還是位置關系,再聯系我們所熟悉的基本圖形,輔助線就呼之欲出了.
以求線段長為例:
初一的時候我們只學過利用全等求線段長,也就是找到與所求線段相等的線段即可.
初二的時候我們學習了用勾股定理求線段長.
初三的時候我們學習了用銳角三角函數與相似求線段長.
這樣根據方法的要求,勾股定理與銳角三角函數都與直角三角形有關,在解決相關問題中通過作垂線,將所求線段放在直角三角形中,就成為了做題的首選.這也就是我們常說的問題切入法.諸如此類的方法很多,例如特殊點切入法、特殊線段關系切入法等.因此教學中教師要注意從這些角度進行滲透,讓學生知其然,又知其所以然.
由于篇幅關系在這里就不再一一介紹了.最后,學習數學是有極強的規律性的,只要我們在教學中善于總結規律,并加以利用這些規律,數學就會越學越簡單.W

