數形結合思想小學數學教學中的巧妙應用

王自豪 廖秀永 張偉

摘要： 在數學教學過程中，“數”與“形”是其中兩個非常基本的概念，并且兩者之間存在一定的聯系。尤其是對于小學生而言，在數學課堂上利用數形結合思想可以將原本比較復雜的數學知識通過更簡單的形式呈現出來，便于學生對數學知識進行更好的理解和掌握。

關鍵詞：數形結合；小學數學；應用

數形結合是指通過數上構形或形中覓數來解決問題的一種思想方法。它既是一種重要的數學思想與方法，又是一種理解數學、學好數學的有效手段。我們在研究數的時候，往往要借助于形的直觀來分析，使數更加清晰、透徹；在探討形的時候，又往往離不開數的本質。因此，在小學數學教學中有機地滲透數形結合思想，通過尋找數與形之間的關系，能使疑惑概念、難解題目豁然開朗，迎刃而解。

一、觀察——培養邏輯思維

1.觀察數形目的明確。小學生喜歡觀察，但不善于觀察，盲目性較大。所以在觀察前，他們明確觀察目的，才會集中注意力，才能收到預期的教學效果。如在教學用割補法推導平行四邊形面積計算方法時，演示教具前，教師應提醒學生觀察：①平行四邊形變成了什么圖形 ？ ②底和高的長度變了沒有 ？ ③平行四邊形的高和長方形的寬，底和長方形的長有什么關系 ？ 通過演示和觀察，學生會很容易理解平行四邊形的面積計算公式。

2 觀察數形本質特征。學生觀察時，常常被一些非本質的表象吸引，教師要引導學生觀察幾何形體的特征，捕捉其本質屬性。為加深學生對平行四邊形特征的認識和比較平行四邊形與長方形的異同，可以拉動長方形活動教具進行演示。拉動長方形的對角，讓學生觀察邊和角的變化，經過演示和觀察，學生可發現：拉動長方形的對角，長方形就變成了平行四邊形，兩組對邊分別平行且相等，內角和是 360°，它和長方形的不同點在于四個角不是直角。再讓學生觀察日常所見鐵拉門格子的實例，學生就易理解平行四邊形的可變特性。

另外，教學時須提供各種變式，不斷變化其非本質屬性，保證其本質屬性，幫助學生認識圖形的基本特征。例如，“只有一組對邊平行的四邊形是梯形”。至于這組平行的對邊的長短、位置，梯形的大小、形狀等則是非本質的。因此，要出示不同的圖形，讓學生辨認，掌握其特征。

二、計算——助力智力發展

（一） 以形助數

所謂“以形助數”，是指老師在講解某些數學知識的時候，僅靠數字講解學生不太能理解。借助幾何圖形的特點，將所要講的知識點更直觀地展現在學生面前。從而將抽象化的問題轉變為具體化的問題。

例1如：一輛汽車從甲地開往乙地，先是經過上坡路，然后是平地，最后是下坡路，汽車上坡速度是每小時20千米，在平地的速度是每小時30千米，而下坡的速度則是每小時40千米，汽車從甲地到乙地一共上坡花了6小時，平地花了2小時，下坡花了4小時。請問汽車從乙地到甲地需要多長時間？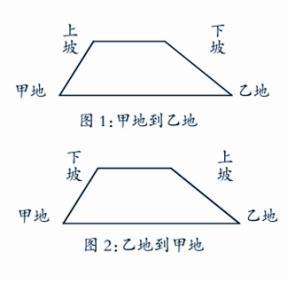

在這道題中，既存在變量，又存在不變量。變量就是上坡路和下坡路隨著汽車行駛的方向而發生改變，當汽車從乙地到甲地行駛時，原先的上坡路變成了下坡路，原先的斜坡路變成了上坡路。而不變量就是這兩個路程汽車行駛的速度都是始終不變的。因此老師在幫助學生解決這道題的時候。可以采用圖形的形式解決，具體如下圖所示：

那么在解決問題的時候，就可以直觀地展現出來。先算出汽車從乙地到甲地的上坡時間，即（40×4）÷20=8（小時），然后算出下坡所花費的時間，即（20×6）÷40=3（小時），而平地所花費的時間是不變的，所以汽車從乙地到甲地所花費的時間是8+3+2=13（小時）。在這道題中，運用圖像將數學中的數量關系、運算都直觀地展現出來。學生比較易于理解，這樣的教學可以在很大程度上提高教學效率。

（二） 以數助形

為了能夠讓學生真正認識數學結合思想，教師應遵從“以數助形”教學原則，讓學生能夠透過圖形掌握其內在數學信息，慢慢養成良好的數學問題解題思維。例如，在《解直角三角形及其應用》一課教學時，教師可采取“以數助形”教學方法，指導學生結合直角三角形角與線段之間、線段之間位置關系和數量關系，進行“形”到“數”的轉換，準確計算出圖形中的數量關系。再如，在《多邊形及其內角和》一課教學時，教師也可指導學生透過多邊形特殊性分析其中數量關系。

例2：已知有一塊長與寬分別是am和bm的草坪，現在要在這塊草坪上修筑一條小路，假設這條小路的寬是1m，余下草坪用m2表示。那么若想增加美感，把原有小路設計為一條寬為1m的彎曲小路，余下草坪面積是多少？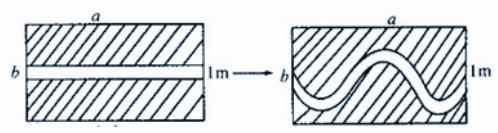

教師在帶領學生解決這一道數學問題時，可先為學生出示相應的圖示，帶領學生透過圖示分析題目本質，了解題目考察的重點內容是矩形面積問題，利用矩形面積=長×寬這個公式，快速求解出正確答案。在上述案例教學中，教師要帶領學生先分析圖示的特殊性，引導學生通過平移圖示發現一個新的矩形，進而通過由“形”到“數”的轉換，快速求出相應答案。

綜上所述，通過對數形結合思想的有效運用，不但可以改變枯燥無聊的課堂氛圍，同時在一定程度上還能不斷帶動學生對于數學課程學習的積極性，使學生在面對問題時可以很快地進行解決。因此，我們應積極地在數學教學中探索數形結合思想的滲透應用方法，從而全面提升教學效果。

參考文獻

[1]季晶.數形滲透思維開花——淺談小學數學教學中數形結合思想滲透策略[J].小學教學參考， 2014（3）

[2]李玉媛.數形結合思想在小學數學教材中的滲透[J].考試周刊，2013（58）