某模塊化槍族導氣裝置動力特性仿真研究

袁 點，張 朋，張 克

(中國兵器工業第二〇八研究所，北京 102202)

某模塊化槍族包含步槍、機槍和短步槍，設計要求步槍和機槍使用相同的活塞、導氣箍、自動機部件，步槍、機槍導氣孔位置相同，以實現模塊化，達到槍族內高比例的零件通用率和相近的動力特性[1-2]。

因槍族槍管長度不同，部分槍型導氣位置、活塞結構存在差異等，造成不同槍型導氣裝置動力特性存在較大差異，通過針對某模塊化槍族導氣裝置動力特性開展仿真研究，應用特定的研究方法，可實現仿真計算與實際試驗結果的高度吻合，便于模塊化槍族的導氣系統參數匹配及后續設計。同時借助仿真研究能避免例如槍管等部件多方案驗證，避免了大量試驗研究工作量巨大，成本過高等弊端。

1 某模塊化槍族內彈道特性研究

1.1 56式7.62 mm普通彈參數

某模塊化槍族使用56式7.62 mm普通彈，該型彈藥主要參數如下：

口徑：7.62 mm；

藥室容積：1.86e-3m3；

彈頭質量：7.75～8.05 g；

發射藥：2/1樟；

裝藥量：1.6 g；

裝藥密度：0.86g /cm3；

發射藥參數如下：

平均燃燒層厚：0.19～0.24 mm；

平均孔徑：0.07～0.15 mm；

平均長度：0.85～1.25 mm；

火藥力：1 000 000～1 050 000 kg·m/kg；

余容：0.9～1 dm3/kg。

1.2 基于遺傳算法的內彈道符合計算

經典內彈道計算是建立在許多假設條件下，實際計算中，許多參數的變化對內彈道的計算結果影響很大且參數變化量多、范圍大，僅靠經驗對內彈道結果進行擬合，很難做到準確修正。

本研究基于遺傳算法，對內彈道參數進行修正，優化參數值，再采用經典內彈道理論對內彈道進行符合計算，實現內彈道計算的精準修正。

1.2.1遺傳算法

遺傳算法(genetic algorithm，GA)是模擬生物在自然環境中的遺傳和進化過程而形成的一種自適應全局優化概率搜索算法。它的思路來源于達爾文的進化論，是模擬生物界遺傳選擇和自然淘汰的生物進化過程的計算模型[3]。

1.2.2內彈道參數修正

內彈道參數中槍膛的橫斷面積S，藥室容積V0，裝藥質量ω，發射藥密度Δ等參數確定。本研究修正的參數為火藥熱力系數θ、次要功系數φ、火藥力f、發射藥弧厚e、發射藥平均長度c、火藥燃燒指數n、火藥燃速u、彈頭重m和火藥余容α等9個參數變量[4]。故優化變量可寫為：

X=[x1,x2,x3,x4,x5,x6,x7,x8,x9]T=

[θ,φ,f,e,c,n,u,m,α]T

遺傳算法以染色體的形式對所有變量進行統一編碼，對自變量沒有限制，適合解決具有多變量的優化問題。本優化模型每個變量均采用長度為20位的二進制編碼串，9個變量組成一個180位長的編碼串。

各修正變量的取值范圍見表1。

該模塊化槍族采用導氣式結構，在內彈道模型計算中，最主要的幾個彈道特性是最大膛壓pm，彈丸出槍口時的膛內壓力pk，彈丸初始v0，內彈道時間t0等， 以上參數對導氣式自動武器的氣室內壓力(導氣式自動武器自動能量來源)影響很大。綜上，本內彈道符合計算是一個多目標優化計算，共有pm、pk、v0、t04個分目標。

對多目標優化問題要想使每個目標函數都達到最優值，一般是很難辦到，通常采用構造一個綜合評價函數，構成單目標優化問題，以求取一個對每個目標來說都相對最優的有效解。

表1 修正參數的取值范圍

本研究采用的優化思路是尋找一組合適的參數使彈道特性計算值與目標值的差盡可能小，故采用平方加權和法構造評價函數，其形式如下：

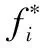
設置遺傳算法的初始種群規模100，交叉概率0.7，變異概率0.05，遺傳代數400。經優化計算得到的目標函數值與迭代次數的關系如圖1，隨著迭代次數的增加，目標函數最小值趨于穩定；計算得到的修正后的內彈道參數值見表2。

以模塊化槍族中的機槍內彈道為計算模型，最終優化得到的內彈道參數值見表3。從表中對比可知，膛口壓強pk誤差2%，其余參數量的誤差均小于1%，內彈道符合計算較合理，與實測值高度吻合，可以用于模塊化槍族的仿真計算。

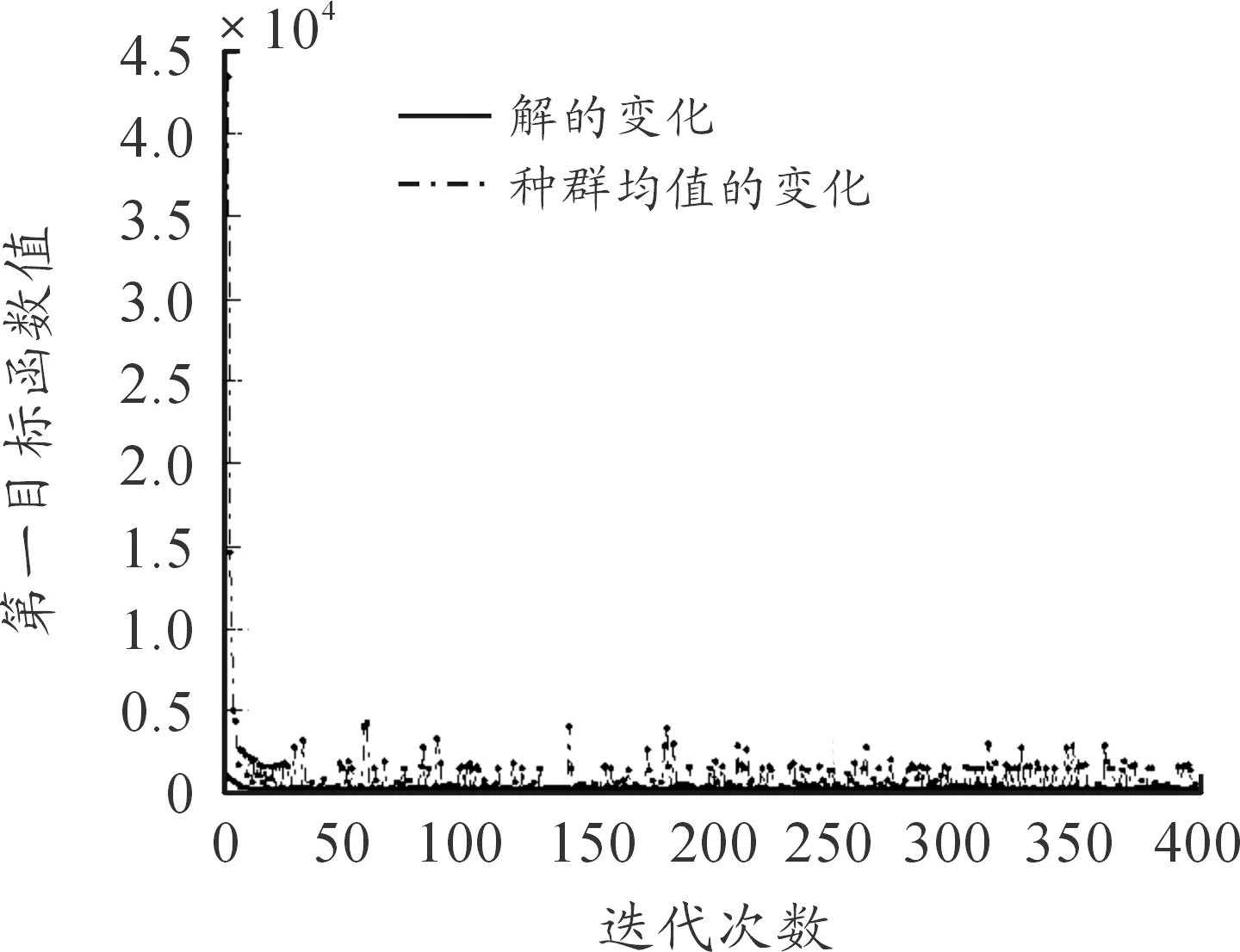
圖1 目標函數值與迭代次數的關系

參數參數值火藥熱力系數θ0.252 64次要功系數φ1.028 5火藥力f93.965發射藥弧厚e/mm1.089 4發射藥平均長度c/mm0.865 32火藥燃燒指數n0.877 69火藥燃速u/(10-9m3/s·kg)7.589 8彈頭質量m/kg7.961 2火藥余容α0.928 27

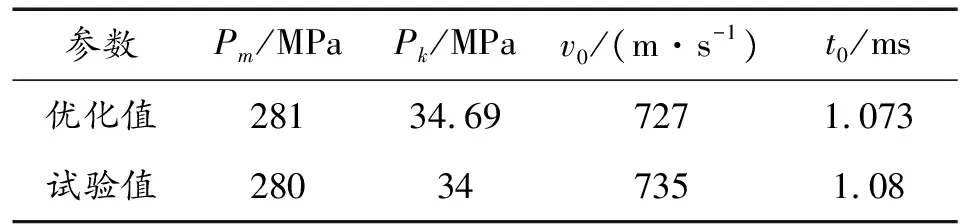
表3 機槍內彈道參數值

1.3 模塊化槍族內彈道計算

已知7.62 mm模塊化槍族槍管長度和導氣孔到槍管尾端面距離，結合已優化出來的內彈道參數量，使用經典內彈道方程組對模塊化槍族內彈道曲線進行計算，得到模塊化槍族詳細的內彈道計算結果見表4。

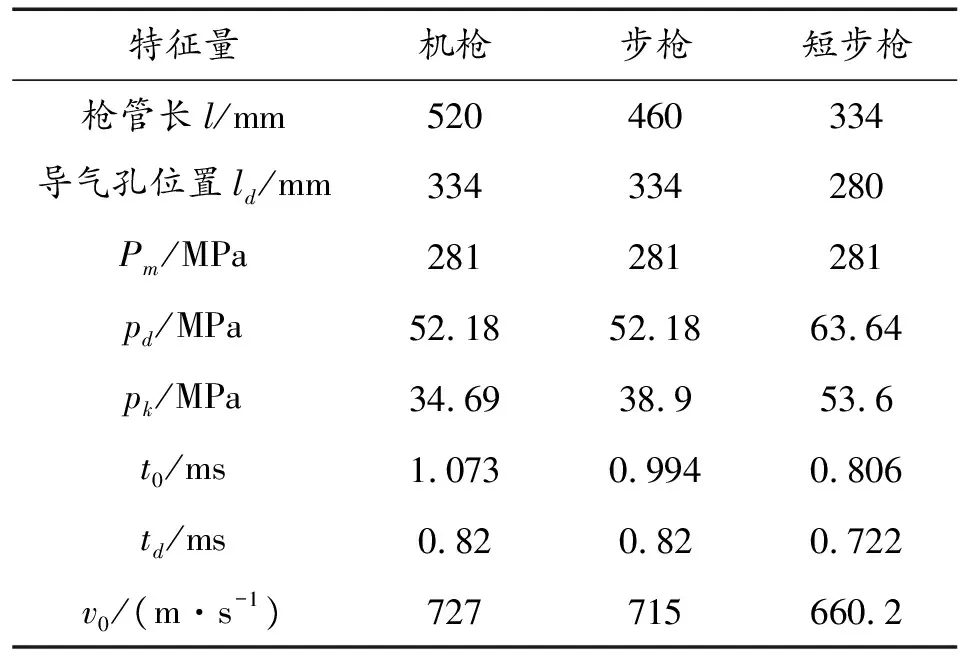
表4 7.62 mm模塊化槍族內彈道計算結果

2 模塊化槍族導氣室壓力計算

導氣室內的火藥燃氣壓力變化規律與膛內火藥氣體變化規律有和導氣裝置結構參數有關。采用布拉文經驗公式描述氣室壓力變化規律為[5]：

式中：pd表示彈丸經過導氣孔位置時的膛內平均壓力；t表示從彈丸經過導氣孔位置時算起的時間，即氣室壓力工作的時間；a表示與導氣裝置結構有關的結構系數；b表示與膛內壓力沖量有關的時間系數。

根據布拉文經驗公式，并對模塊化槍族的導氣裝置進行分析，編寫出氣室壓力的計算程序，計算可得導氣室內火藥燃氣的壓力ps隨時間t的變化關系如圖2所示。

圖2 氣室壓力時間曲線

從圖2可知，機槍與步槍的最大氣室壓力為36.23 MPa，短步槍的為42.13 MPa。

3 模塊化槍族虛擬樣機模型仿真研究

因7.62 mm模塊化槍族采用相同的自動機結構，故本研究主要以步槍為研究對象，建立虛擬樣機模型， 將已完成設計的三維模型通過接口文件導入ADAMS中，在添加載荷、約束、材料、質量屬性和接觸關系后，形成某模塊化步槍的虛擬樣機模型[6-7]，如圖3；分別將由Matlab計算出的各槍型氣室壓力施加于模型，作為自動機運動的動力來源。

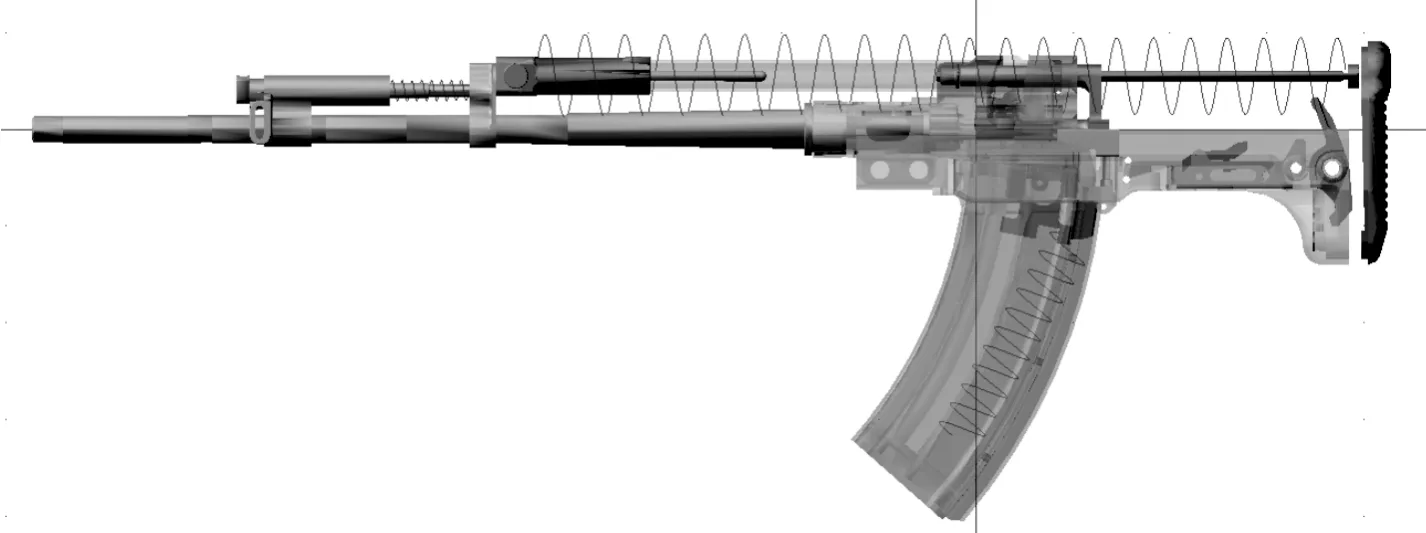
圖3 模塊化步槍虛擬樣機模型

在本仿真模型中，為提高計算效率，仿真只計算一次自動機運動循環，彈膛內已裝入一發彈，彈匣內裝一發彈，一次自動機循環完成拋殼和供彈全過程。其自動循環可詳分為后坐和復進兩個階段，后坐過程動作為：開鎖前行程→開鎖→開鎖后自由行程→抽殼→拋殼→槍機慣性后坐→后坐到位緩沖作用。復進過程動作為：緩沖簧加速→擊錘與槍機一起復進→擊錘掛上阻鐵→槍機空行程→推彈入膛→機頭預轉→閉鎖→閉鎖后自由行程。

自動機運動的動力為氣室壓力，其施加方法為：由Matlab計算出的各型槍的氣室壓力曲線，然后再將載荷導入到ADAMS中，氣室壓力乘以活塞的橫斷面積即為活塞受到的載荷力。綜上，ADAMS仿真計算出某7.62 mm模塊化槍族的自動機運動曲線如圖4所示。

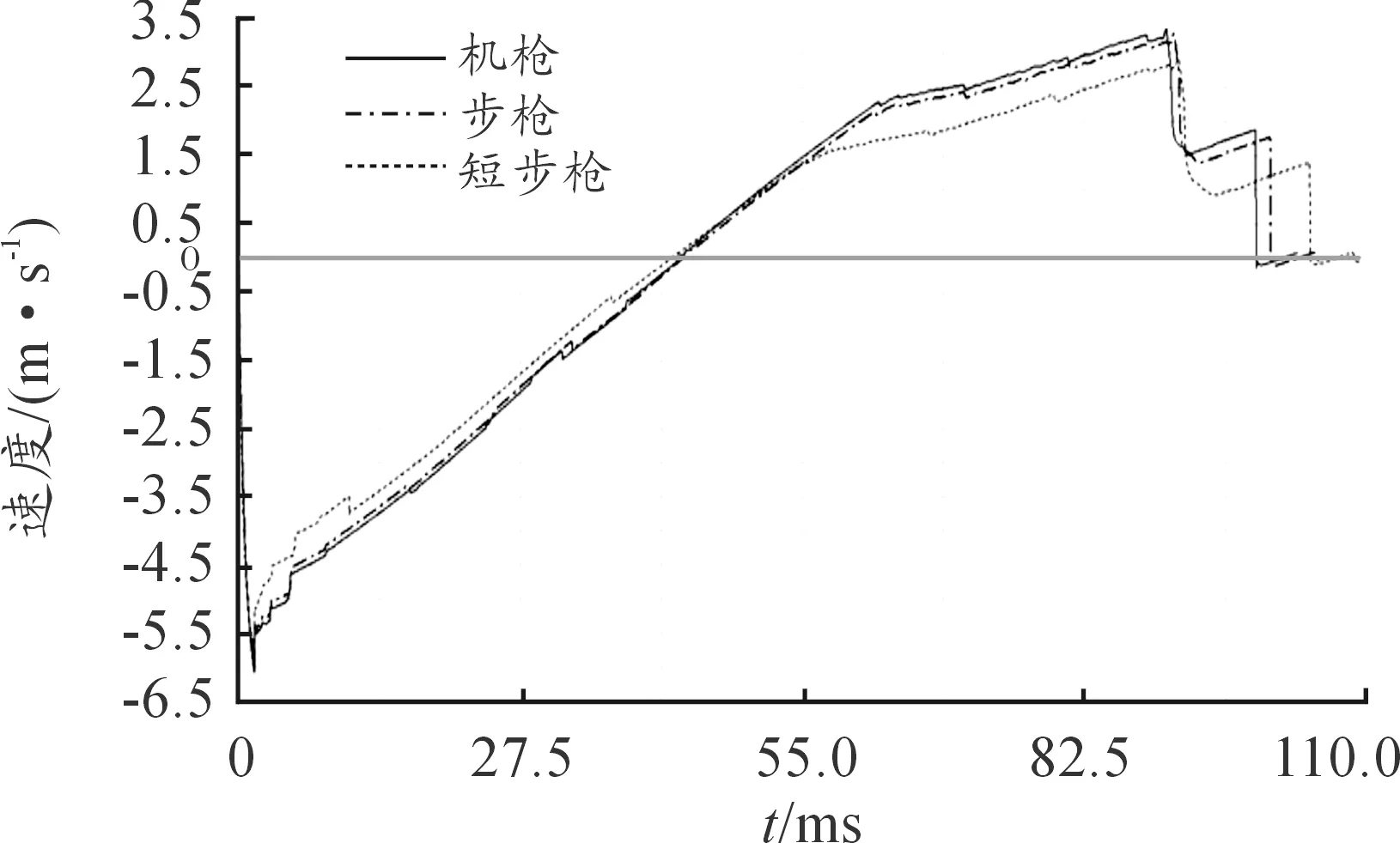
圖4 自動機運動曲線

在某設計結構下，某7.62 mm模塊化槍族的自動機運動仿真參數和測試參數如表5所示。從表5可知，模塊化槍族的仿真結果與測試結果較為吻合，尤其是槍機框開鎖前最大后坐速度與測試值誤差很小。可用于后續優化7.62 mm模塊化槍族的導氣裝置結構參數等工作。

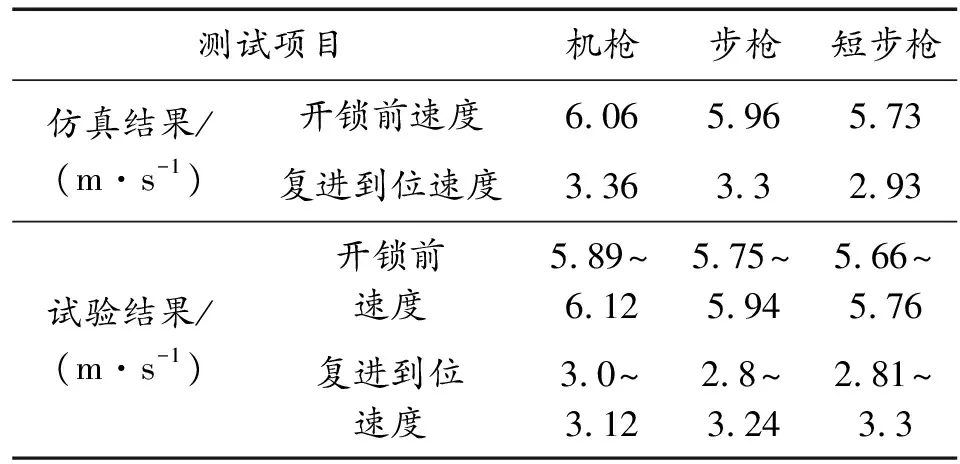
表5 自動機運動速度仿真與測試結果

4 結論

1) 本研究對某7.62 mm模塊化槍族內彈道使用遺傳算法進行了驗證計算，可有效縮小內彈道理論計算與試驗值間差異；

2) 仿真得到的自動機運動曲線結果與試驗測試結果高度吻合，建立的氣室壓力計算模型和虛擬樣機模型比較合理。

3) 該仿真研究可較大地提高后續科研工作研究效率，減少加工及試驗成本。

4) 該研究方法亦可用于其他口徑、其他類型導氣式武器的仿真研究，具有參考價值和指導意義。