測試性試驗樣本量按比例分層抽樣補充分配方法
趙 靖,吳 棟
(1.工業和信息化部電子第五研究所, 廣州 510610; 2.電子信息產品可靠性分析與測試技術國家地方聯合工程研究中心, 廣州 510610; 3.廣東省電子信息產品可靠性技術重點實驗室, 廣州 510610)
隨著裝備五性水平的逐步提高,測試性水平越來越受到重視,裝備測試性水平已經成為了木桶的短板,測試性指標的驗證和評估也越來越受到各方重視,測試性驗證試驗的重要性也愈發彰顯[1-5]。測試性驗證試驗包括測試性非實物驗證試驗和測試性實物驗證試驗[5],本研究所指測試性試驗是指測試性實物驗證試驗。
測試性試驗方案是試驗開展的最基本依據,主要有以下3個方面內容[1]:
1) 試驗樣本量的確定方法;確定試驗所需要注入的故障模式樣本總數,即確定試驗的總規模;
2) 樣本量分配;將試驗樣本量分配到裝備的故障模式中,即確定每個故障模式所注入的次數;
3) 故障模式抽取:即建立備選樣本庫;將所有樣本的詳細故障注入信息列出,供試驗選取;
因此樣本量分配是測試性試驗的關鍵一環,直接影響到試驗結果的準確性,有必要對樣本量分配的方法進行深入研究。
現行的國家軍用標準中有關裝備測試性試驗樣本分配的方法較少,詳細規定了試驗樣本分配方法的只有《GJB2072—94 維修性試驗與評定》,其中“附錄B 維修作業樣本的選擇與分配方法(補充件)”給出了兩種可供參考的維修作業樣本的分配方法,分別為按比例分層抽樣的分配法和按比例的簡單隨機抽樣分配法。雖然該方法針對的是維修性試驗,但該標準在“附錄C 測試性試驗的一般方法”中要求測試性試驗的模擬故障樣本的分配和模擬與維修作業樣本分配和故障模擬相同,因此很多裝備的測試性試驗樣本分配方法參考了該標準。另一標準《GJB 8895—2017裝備測試性試驗與評價》附件J提供了與GJB2072—94完全相同的按比例分層抽樣的分配法做參考。
但是,在采用此兩個標準提出的按比例分層抽樣的分配法且使用固定樣本量的方案時,在多數情況下會出現分配完畢的樣本總數不等于規定的固定樣本量的情況,導致樣本分配失敗,需要手動進行補充分配,并且這兩個標準給出的示例中同樣默認進行了手動補充分配,而對于該補充分配方法兩個標準都未提及。
目前測試性試驗的樣本總量一般較大,故障模式總量也較大,例如某型雷達功能電路級故障模式多達3112個,某型供電處理機功能電路級故障模式多達3160個。因此當采用該方法在使用計算機輔助分配時將存在障礙,且當樣本量較大時,手動補充分配存在很大的執行難度,也難以保證分配的準確度。本研究對該方法進行了詳細分析,根據按比例分層抽樣的分配原則,給出基于最小誤差排序的補充分層抽樣分配方法,并在計算機上予以實現。
1 按比例分層抽樣分配法
GJB2072中給出的按比例分層抽樣分配法是以故障率為基礎進行的分層抽樣,下面舉實例說明該方法。假設某產品的故障模式如表1所示,按比例分層抽樣分配法的具體實施步驟如下:

表1 某產品按比例分層抽樣分配樣本示例
a) 列出受試產品的組成,包括LRU、SRU、功能電路等;
b) 列出受試產品每個層次的所有故障模式;
c) 列出每個故障模式的故障率λi;
d) 統計所有故障模式的故障率之和λT;
f) 以初步樣本量n作為總的樣本量,一般設置總的預選樣本量N為初步樣本量的4倍,列出每個故障模式的預選樣本量Ni=4n×Cpi,進行四舍五入后取整數,試驗時,試驗樣本要從預選樣本中選取。
g) 列出每個故障模式的樣本量ni=n×Cpi,并取整。
通過本例可以看出,根據該方法分配完的樣本量總數比原先規定的總樣本量少1個,總預選樣本量也比規定的總預選樣本量少1個,總樣本量沒有被完全分配。
在某些情況下也會出現總預選樣本量比規定的多一些。出現這種情況是由于每個故障模式的相對發生頻率Cpi在與初步樣本量n相乘時通過四舍五入后,出現了舍入誤差,從而出現部分故障模式的樣本量少于或多于應分配的樣本量。
根據第g步中公式可知,按比例分層抽樣前后的樣本量偏差Δn與初步樣本量n和相對發生頻率Cpi有關,而Cpi與故障模式的故障率和故障模式總數有關,下面對樣本差Δn與故障模式總數Nλ和樣本總量n的關系進一步進行分析,首先構造1個產品,故障模式總數為2 000個,樣本總量n為故障模式總數Nλ的0.2倍到2倍(令該倍數為K),即從400個到4 000個,然后構造每個故障模式的故障率,由于不同產品的故障率的分布各不相同,在此采用了常見的均勻分布,也為了便于實現,采用偽隨機序列對故障率進行構造,所構造的2 000個故障模式的故障率分布如圖1所示。

圖1 2 000個故障模式的故障率分布
按GJB2072的按比例分層抽樣法進行抽樣,抽樣結果如圖2所示,從本例抽樣結果可以得到,當K小于0.24時,分配的樣本量均為0,這是由于樣本總量n相對于故障模式總數K過于小,導致在四舍五入后,全部故障模式的樣本量ni均為零;當K逐漸增大,分配的樣本總量也逐漸增加,直至當K大于0.4時,抽樣結果才接近于初步樣本量n,但是仍與初步樣本量n存在偏差,此偏差由四舍五入所導致。
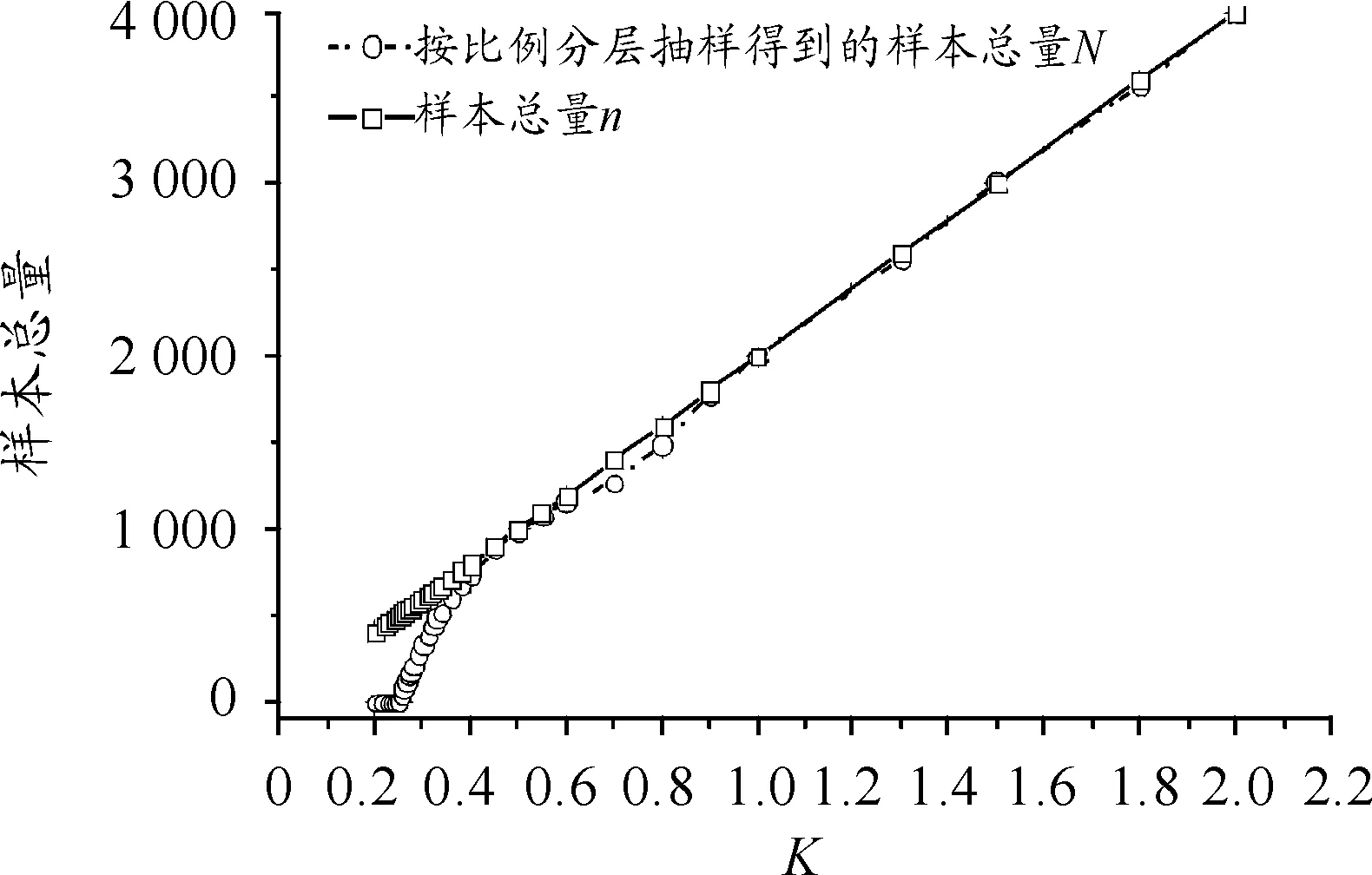
圖2 按比例分層抽樣分配結果
總結以上分析可知,GJB2072所提供的按比例分層抽樣法在K的適用范圍上存在局限,而且抽樣結果往往與樣本總量n存在偏差,導致抽樣失敗。而標準中并未提及補充抽樣的方法,默認進行了手動補充抽樣。本研究提出基于最小舍入誤差排序的補充分層抽樣分配法,不僅每次抽樣能將樣本總量完全分配,并且適合用于計算機編程實現自動抽樣分配。
2 基于最小舍入誤差排序的補充分層抽樣分配法
按比例分層抽樣分配法的基本原則,是對故障率高的故障模式分配多的樣本,對故障率低的故障模式分配少的樣本。為了滿足該抽樣原則,本章給出基于最小舍入誤差排序的補充分層抽樣分配法。
補充分配方法的流程框圖如圖3。
首先,按照GJB2072中的按比例分層抽樣分配法進行樣本量的分配;若出現分配完的樣本總數不等于初步樣本量n,則按照下述方法進行補充分配:
每個故障模式所分配的樣本量浮點數為:

(1)
對每個故障模式所分配的樣本量浮點數進行四舍五入取整:
(2)
分配完的樣本總數與初步樣本量的樣本差為
∑ni-n=Δn
(3)
記每個故障模式的舍入誤差為:
(4)
舍入誤差σi為正,代表其經過四舍五入后誤差被舍去了,導致了樣本量不足;舍入誤差σi為負,代表其經過四舍五入后被進位了,導致了樣本量超額。
根據樣本差Δn進行分別討論:
1) 若Δn<0:
a) 需要對舍入誤差σi為正的故障模式進行比較和排序,舍入誤差σi最大的前|Δn|個故障模式需要進位,即其樣本量增加1個;
b) 若舍入誤差σi為正的故障模式數少于|Δn|個,則需要對所有故障模式的樣本量浮點數加0.5,保證全部進位,此時樣本差記為Δn′;
2) 同理,若Δn>0:
a) 需要對舍入誤差σi為負的故障模式進行比較和排序,舍入誤差σi最小的前Δn個故障模式需要退位,即其樣本量減少1個;
b) 若舍入誤差σi為負的故障模式數少于Δn個,則需要對所有故障模式的樣本量浮點數減0.5,保證全部退位,此時樣本差記為Δn′;
經過以上計算后,若存在nσ個故障模式的舍入誤差在計算精度內完全相同,且樣本量還需要減少或增加少于nσ個時,若給這nσ個故障模式每個都分配一個樣本數時,將會出現分配的樣本總數超過初步樣本量n,則對這nσ個故障模式進行隨機排序,對隨機排序靠前的故障模式各增加一個樣本量直至分配的樣本總數等于初步樣本量n。
本方法主要原理是對每個故障模式的舍入誤差進行排序,舍入誤差越大的故障模式越應當補充1個樣本,并對多種情況分別進行處理,能夠適應多種實際情況。
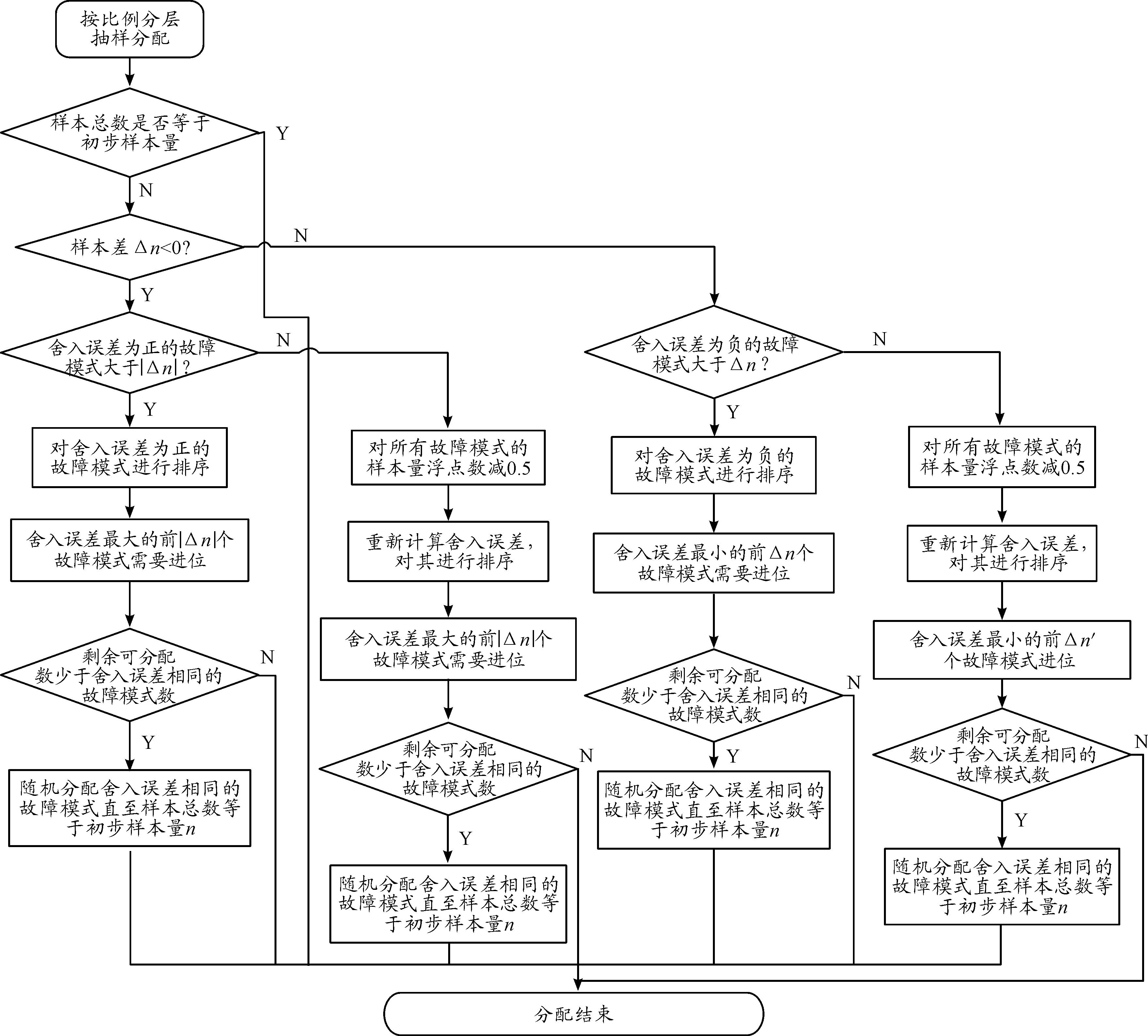
圖3 基于最小舍入誤差排序的補充分層抽樣分配法流程框圖
3 軟件實現及驗證
根據以上算法和流程,項目組在Matlab開發環境下開發了測試性方案設計軟件,實現了樣本總量的計算、樣本量自動分配、自定義補充樣本等多項功能,能夠用于測試性方案的設計。對本軟件的樣本量分配功能進行如下實驗以進行驗證:構造5個產品,其故障率采用偽隨機數進行構造,故障模式總數分別為100、500、1 000、2 000、4 000,對此5個構造產品分別進行樣本量分配,令樣本總量與故障模式的總數的比值K的范圍為0.4 圖4 兩種抽樣方法實驗結果 圖5 軟件抽樣結果 綜上所述,本研究提出的基于最小舍入誤差排序的補充分層抽樣分配法綜合考慮了多種可能因素,按照按比例分層抽樣原則對樣本差進行了補充分配,解決了GJB2072中提供的按比例分層抽樣分配方法存在的抽樣結果中樣本總量與預先確定的初步樣本量不相等的問題,以往只能通過手動進行補充樣本,補充方法具有主觀隨意性,本研究設計了軟件實現自動的補充抽樣分配,使得抽樣分配結果準確、合理,實驗結果也驗證了本方法的有效性和適應性。同時研究也發現,按比例分層抽樣法本身具有適用范圍限制,即其不適合用于樣本量遠小于故障模式總數的情況。本軟件和方法能應用于型號項目的測試性試驗方案設計中,為推廣采用按比例分層抽樣法進行了鋪墊,具有廣闊的應用前景。

4 結論

