流程圖支持下的計算思維培養實踐研究

郁曉華 王美玲

【摘要】? ?? 當前K-12階段的計算思維培養中缺乏一種思維加工的輔助工具，用以記錄并顯性化呈現學習者的思維從識別問題到形成方案的全過程。這使得教學很難深入思維發展的細節部分，做出有針對性的指導和評價，使得計算思維培養的效果存在局限。本文基于工程設計的問題解決視角，從問題識別與分解、系統抽象與方案設計優化、方案實現和問題遷移四個階段探討了流程圖支持下的計算思維教學過程，并對來自上海某中學6年級～8年級的19名學生開展了一個學期的教學實踐，結合流程圖評價、能力前后測、作品評價、作品問答反饋四種方式，從認知和操作層面以及非認知層面對他們的計算思維發展進行評價。實驗結果初步顯示，學生的計算思維在流程圖的支持下得到了有效提升，并且流程圖得分高和流程圖得分提升幅度大的學生其提升效果更加顯著。

【關鍵詞】? 計算思維;流程圖;程序設計;問題解決;K-12;評價;人工智能;信息技術;核心素養;信息素養

【中圖分類號】? G642.0? ? ? ?【文獻標識碼】? A? ? ? ?【文章編號】? 1009-458x（2019）9-0083-09

引言

計算思維作為一種解決問題的重要技能（Wing， 2006），被認為是與閱讀、寫作、計算一樣的當代學習者自我發展必備的基本素養之一（Freeman， Adams Becker， Cummins， Davis， & Hall Giesinger， 2017），也是人工智能（artificial intelligence， AI）時代的獨特能力要求（王本陸， 等， 2018）。2017年7月，國務院（2017）印發的《新一代人工智能發展規劃》明確了新時代下人工智能發展的戰略目標以及AI人才培養的競爭焦點。這一文件的出臺引發了教育界對于人工智能教學和編程教育下計算思維培養的關注，尤其是新一輪發展的落腳點由高等教育向K-12階段的發展遷移（Bocconi， Chioccariello， Dettori， Ferrari， & Engelhardt， 2016）。計算思維的培養強調為學習者建立一種以計算的視角和方法參與問題解決全過程的全新能力（郁曉華， 等， 2018），涉及思維加工過程在問題的識別與理解、問題的分解與重構、方案的設計與實施等多個環節的綜合發展。但在以往計算思維培養模式下，學習者在解決問題時思維加工的過程往往是直接隱含在編程開發（方案的實施環節）中，不被重視、被弱化，甚至被忽略，而學習者計算思維的發展情況又是以最終的編程制品作為評價的主要依據或者是唯一的依據。由于最終的編程制品只能展現學習者思考的結果而不能呈現學習者思考的過程和變化，這種重結果輕過程的培養模式并不利于師生對計算思維發展細節的把握，也與計算思維培養的本質不符。由此帶給我們的思考是，能否引入一種思維加工的輔助工具，用以記錄并顯性化呈現學習者的思維從識別問題到形成方案的全過程，從而更好地幫助師生理解學習中的過程性信息，進而有針對性地加以評價和調整，使計算思維的發展回歸核心本質。在本研究中，流程圖就被選作這樣一種計算思維加工過程的可視化承載工具。

一、流程圖作為計算思維加工過程的可視化承載工具

（一）計算思維培養中對思維加工過程的忽視

編程教學作為目前培養計算思維的最主要手段，在全世界范圍內得到了廣泛的實踐和多元化的發展。比如，美國麻省理工學院媒體實驗室（MIT Media Lab）終身幼兒園研究小組（Lifelong Kindergarten research group）開發了旨在培養計算思維的Scratch創意計算課程，該課程體系下每個學習單元中都有不同的情境和任務，學習者經過自主思考后用Scratch探索開發完成任務（王旭卿， 2014）;DEVTECH研究小組設計的KIBO課程，學習者在操作動手的過程中加強對計算思維概念的理解（Sullivan， Bers， & Mihm， 2017）。Wang等（2014）提出通過有形編程工具培養計算思維，教學分為演示、練習、創造開發和訪談四個環節，學習者在有了一定的操作基礎后進入創造開發環節，自主設計開發自己喜歡的作品;在Atmatzidou等（2016）提出的基于教育機器人的計算思維培養模式下，學習者在工作表的指導下以小組合作的形式由易到難掌握基本操作，開發機器人程序，培養計算思維核心能力。然而，從工程設計的視角看（Massachusetts Department of Education， 2006），這些研究普遍把培養的重心放在方案實現的環節，教學組織上大多是從識別與理解問題直接就進入代碼編程實現的階段，缺乏對問題如何從現實轉為抽象的觀察和指導;在此操作中，學習者對問題進行分解和重組，進而進行系統抽象和建模，形成設計方案的思維加工過程并沒有很好地被凸顯出來，大多被隱沒在具體的程序編寫當中。實際上，計算思維在實踐運用中繼承了工程思維的統籌特性（郁曉華， 等， 2018），圍繞問題的解決，學習者要能發現主客體的屬性以及它們之間的各種價值邏輯，并將這些關聯復合在一起加以提煉抽象（王榮良， 2008），同時還要能識別和評價出最佳解決方案。培養學習者的計算思維能力并不是為了培養將來的程序員，而是要幫助他們更好地掌握解決問題的思維和方法，建立觀察和理解周邊世界的全新視角（Grover & Pea， 2013; 李鋒，2018）。在計算思維的核心內涵下，強調解決問題的過程更重于問題解決的結果。因此，從工程設計角度出發的計算思維教學過程應至少包括識別問題、分解問題、系統抽象、方案設計與優化、方案實現五個部分。其中，前四個部分體現了思維的加工過程，最后一個部分則呈現了思維發展的結果。程序開發只是對思維結果的一個很好的表達和呈現，而在分解重構問題、形成方案的過程中還亟須一個思維加工過程的承載工具來協助學習者進行思路的梳理和建構，記錄并可視化他們解決問題過程中從現實向抽象的過渡與轉變。

（二）流程圖與計算思維過程的可視化

計算思維培養中思維加工過程的弱化甚至缺失，一方面是由于在教學設計當中未受到重視，另一方面是由于沒有尋找到適合的思維承載工具。在已有研究中，主要是通過訪談或調查問卷的形式呈現學習者的計算思維加工過程。比如，布倫南和瑞斯尼克（Brennan & Resnick， 2012）采用基于作品的訪談法了解學習者開發作品的過程性信息，但這種形式耗費大量時間，而且要求學生保持對開發過程的準確記憶，訪談過程中容易出現部分學習者存在表達障礙等情況;科爾克馬茲等人（Korkmaz， ?akir， & ?zden， 2017）通過編制量表來評價學習者計算思維技能的發展，但這種形式容易產生測驗誤差，對低年級學習者易造成理解困難。思維可視化的出現，有力推動了學習者的“思維發聲”，運用可視的技術手段可以將他們隱性的思維過程清晰地呈現出來（趙慧臣， 等， 2014），以協助對學習者的思維加工過程進行理解和認識。思維可視化通過豐富的圖示符號展現了主題元素之間的關系邏輯和過程演繹，近年來開始逐漸納入計算思維的培養環節之中。例如，Chen等（2015）在計算思維的培養過程中引入概念圖幫助教師建構教學問題，有效提升了學習者的計算思維。Repenning等（2016）指出思維導圖可以作為輔助計算思維培養的工具，將概念捕獲為節點和鏈接，學習者通過使用思維導圖可視地組織信息，支持問題表達這一概念化的過程。在各種圖示方式中，流程圖以其特性更適合用于繪制解決問題的過程（劉濯源， 2014），當前編程教學實踐中的應用非常多。例如，基于流程圖的編程環境中將流程圖直接作為一種設計工具，幫助學習者尤其是編程初學者實現系統的開發;通過減少對編程語言和語法的關注，將設計聚焦在解決問題的過程上（Crews & Ziegler， 1998; Powers， et al.， 2006; Hooshyar， Ahmad， Shamshirband， Yousefi， & Horng， 2015）;在正式編寫代碼之前，引入繪制流程圖的環節，可以促進學習者理解程序的邏輯關系，提升編程的學習效果（Hu， 2003）。基于此，流程圖可以很好地作為計算思維過程抽象表達的形式化工具，以有效展現問題解決的細節分解和過程演繹（Gouws， Bradshaw， & Wentworth， 2013）。此外，還可以作為一種評價工具，以考察學習者解決問題的思考過程（Chen， et al.， 2017），但現有實踐在流程圖與計算思維的結合上并不多見。

二、流程圖支持下的計算思維培養實踐

（一）計算思維在流程圖中的體現

有效的培養實踐扎根于對計算思維的深度理解。數十年來，諸如周以真（Wing， 2006）、美國師生創新技術體驗機構（Innovative Technology Experiences for Students and Teachers，ITEST）計算思維工作組（Allan， et al.， 2010）、計算機科學教師協會（Computer Science Teachers Association， CSTA）與美國教育技術協會（International Society for Technology in Education，ISTE）（2011）、美國麻省理工學院媒體實驗室的布倫南和瑞斯尼克（Brennan， et al.， 2012）、南安普頓大學的塞爾比等（Selby & Woollard， 2013）以及中國教育部（2018）等很多組織和研究人員都對計算思維的含義進行了不同闡釋。盡管這些闡釋中關于計算思維所包含的內容和評估計算思維發展的策略不盡相同，但都普遍認為計算思維是一種關于問題解決的復合思維能力，包含計算視角下解決問題的多個要素——問題識別、問題分解、抽象、算法和邏輯等。而選擇的思維承載工具只有能很好地對這些要素加以展示，才能有效呈現問題解決思維的形成與演變過程。本研究中，流程圖的使用與計算思維要素間的映射關系如表1所示。

（二）教學實踐的設計

計算思維是一種建構性思維，需要將解決問題的思維轉化為一系列計算機可以理解并執行的過程，再進一步建立可自動化處理的計算系統。從認知的角度看，計算思維與問題求解密切相關（龔靜， 等， 2018），計算思維的提升依賴于持續的發現和解決問題的過程，即從一個問題開始提出解決這個問題的理論和方法。隨著最初的問題解決會產生新的問題，然后提出新的解決方案，以此循環往復。這種“從問題到問題”的原則對培養學習者的計算思維能力具有一定的參考價值（Chen， et al.， 2015）。本研究中教學的開展基于工程設計的問題解決視角，圍繞項目主題，使用流程圖作為“思維發聲”支架，聚焦于學習者的思維加工過程和方法習得。整個教學過程如圖1所示。

1. 識別問題與分解問題

每個教學項目本質上就是蘊含在實際生活情境中的一個大的問題。教學從學習者熟悉的生活場景或現象導入，使他們能很方便地結合自身的認知經驗識別出問題的主題，從而將思維加工聚焦于從情境中抽象出待解決的問題并加以分解細化。在這個過程中，學習者可借助流程圖的不同等級逐漸呈現他們理解問題的層次，以及他們如何將一個大問題分解為不同粒度的問題和對象的思維過程。

2. 系統抽象與方案設計優化

學習者自主思考，由簡單、基礎的子問題著手，并借助流程圖中的框線和符號逐漸抽象、設計問題解決的計算邏輯，最終建立起系統化的解決方案。在此過程中，雖強調學習者探索的主體作用，但教師適當的引導以及與同伴的交流互動也同樣不可或缺。學習者通過反思不斷更新解決問題的思路，進而不斷優化自己的流程圖設計，即系統的程序邏輯，發現最佳的問題解決方案。這一階段所形成的流程圖，不僅呈現了學習者抽象和優化問題解決系統的思維過程，也為下一步實現方案的具體程序開發提供指導。教師可以根據學習者繪制的流程圖了解他們解決問題的思路，還可以將其作為評價學習者計算思維發展的重要依據。

3. 方案實現

學習者在繪制流程圖的基礎上，使用各類程序開發工具實現問題解決方案的開發，在呈現思維發展結果的同時，也驗證程序邏輯的可行性和效率。學習者在完成一個子問題后，再以同樣的方式進行下一個更深層次子問題的解決。通過這種問題邏輯的逐層疊加、從簡單情境到復雜情境的螺旋式上升方式，最終完成整個項目問題的工程方案設計與開發。

4. 問題遷移

問題遷移是計算思維培養不可缺失的一環，是促使項目習得的思維過程和解決方法真正吸收內化進而遷移運用的一步。在每個項目結束后，通過反饋問答，學習者被要求進一步根據程序的運行結果回看流程圖的計算邏輯，總結擬定的計算邏輯在實現過程中所做出的調整及其原因，同時提煉自己在項目開發過程中對解決方案的抽象過程，思考當前問題的解決模式可否應用于生活中的其他問題情境，又需要做哪些改變。

（三）教學實踐的開展

1. 教學實踐過程

本研究的實驗對象為上海某中學6年級～8年級的學生，共19人（6年級5人，7年級8人，8年級6人），研究人員利用課外興趣拓展課對他們進行了為期一個學期的流程圖支持下的計算思維培養實踐。在教學中，流程圖作為思維過程的承載工具，對流程圖的使用遵守美國國家標準化協會（American National Standards Institute， ANSI）所提出的規范，而App Inventor（一款在線Android可視化編程工具軟件）作為思維結果的呈現工具。研究在項目學習前首先對參與實驗的學生進行了有關流程圖使用的教學，然后依次開展了涂鴉畫板（4課時）、躲避障礙物（8課時）、手機通訊錄（6課時）三個主題項目的教學，主題復雜度依次遞增。

2. 實驗評價方式及其數據處理

計算思維的能力培養涉及認知層面與操作層面。此外，Snow等人（2017）指出測評還需要從認知和非認知角度進行。基于計算思維概念的復雜多元性，單一的評價手段很難全面呈現學習者計算思維的發展情況，因此本研究借鑒以往研究中較為成熟的經驗和方法，整合了流程圖評價法、能力測試題（前后測法）、作品評價法和作品問答反饋分析法四種評價方式。

（1）流程圖的數據

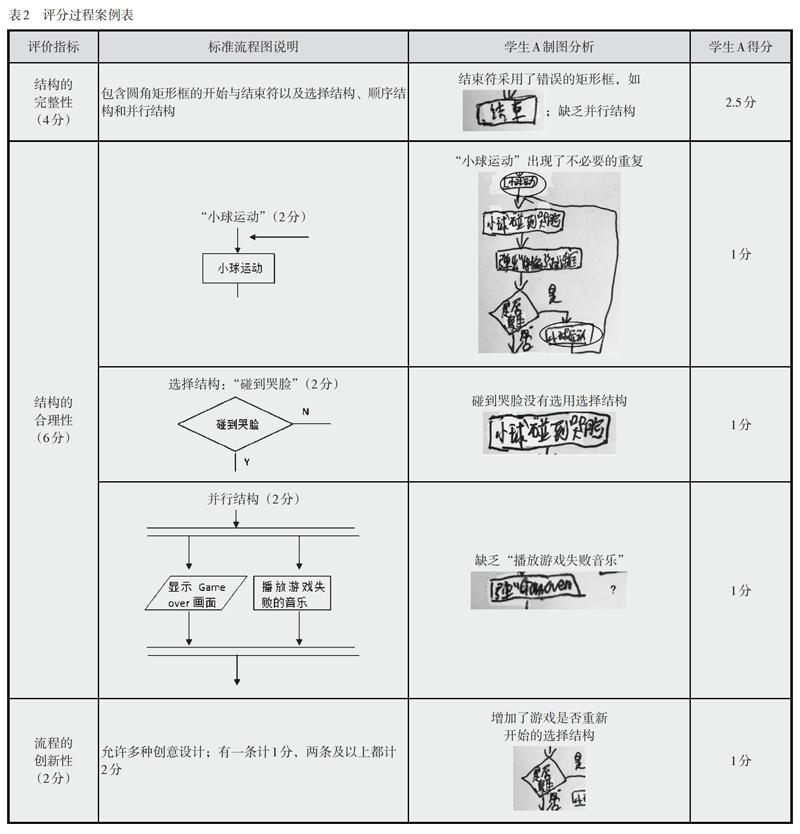
評分員在預設的標準流程圖基礎上分別對學生在三個項目中所繪制的流程圖進行評分，每個項目滿分為12分（如表2所示）。評分規則為：①流程圖結構的完整性，即符號的選用是否正確，是否包含開始結束符，是否包含解決問題所必要的一些結構;②流程圖結構的合理性，即所示流程邏輯是否清晰，是否能夠有效地解決問題;③流程的創新性，即是否包含一些標準之外的獨特設計。流程圖的得分將客觀反映學生計算思維的綜合發展情況。

（2）前后測的數據

本研究參考Román-González等（2017）所編制的計算思維測試題，在教學前后分別進行了前后測。本套測試題是依靠計算的基本概念和使用編程語言的邏輯語法來制定的，由28道單選題組成，適用于5年級～10年級的學生，圖2是翻譯成中文后的計算思維測試題目示例及其說明。參照測試題自身的設置，結合本研究對計算思維的設定，測試結果將從算法、邏輯思維和抽象三個角度來客觀反映學生的計算思維在認知層面的發展變化。

（3）App作品的數據

研究將學生所提交的App作品下載安裝并進行試用，以獲取學生作品相對于教師所要求功能的完成情況，以及學生作品中功能的拓展創新情況，從而了解學生的計算思維在操作層面的發展變化。

（4）作品反饋問答的數據

研究通過作品反饋問答收集學生對參與項目學習的自我評價，對所學問題解決的計算技術與方法的表述，以及對這些技術和方法可遷移用在學習或生活中哪些方面的思考。整理學生的這些觀點或看法，可對其計算思維在教學后在解決問題策略、理解問題發散性等非認知層面的變化有所了解。

三、流程圖支持下的計算思維培養實踐評價

隨著三個項目的教學實踐推進，流程圖的得分直接映射了學生的計算思維在問題識別、問題分解、問題解決、創意拓展等方面的綜合發展。研究還進一步根據學生流程圖的得分對學生繪制流程圖的能力水平進行了分組，再結合其他三種評價方式探究流程圖支持下不同組別的學生計算思維發展的差異，以及在非認知層面的發展影響。

（一）計算思維認知和操作層面的發展評價

1. 對流程圖的分析

兩位評分員基于研究設定的評分細則，分別對19名學生在3個項目中繪制的流程圖進行了評分。評分的斯皮爾曼相關系數分別是，項目一0.756，項目二0.743，項目三0.875，評分一致性較高。因此，可將兩位評分員對每位學生評分的平均值認定為該生在該項目流程圖上的最終成績。各年級學生在三個項目上流程圖的平均得分情況如表3所示。

從表中不難看出，學生在經歷了項目1和項目2的學習后，到項目3的學習時三個年級學生的流程圖得分都有了明顯的提升，即計算思維綜合能力得到了有效發展。

2. 對前后測的分析

前后測試數據顯示，無論從整體上還是分年級段，學生的計算思維后測平均成績均高于前測。可見，經過了一學期的項目教學后，學生的計算思維能力得到了提升。將學生在三個項目中的流程圖得分求平均值后與后測成績做相關分析，皮爾森系數為0.714，呈現出顯著的正相關關系，說明學生計算思維能力的提升與流程圖的使用相關聯。

根據流程圖得分的高低，研究將學生分為高、低兩組（三個流程圖平均得分位于前50%和后50%），排除前后測數據無效的3人后每組8人，高分組學生主要分布在6年級、8年級，低分組主要是7年級學生。兩組學生計算思維的各個維度在前后測中的差異如表4所示。在抽象、邏輯以及總成績方面，高分組進步幅度均大于低分組，而且采用配對樣本T檢驗可以發現高分組在這三方面的提升是顯著的，即流程圖繪制越好計算思維分數提升幅度越明顯，說明流程圖的支持能夠有效促進學習者計算思維的發展。這與已有研究的觀點相符，流程圖能夠幫助學生將他們思考問題的過程顯性化呈現出來從而支持思維表達，提高學生的認知能力（趙慧臣， 等， 2014），并且流程圖的使用與計算思維要素之間還存在緊密的映射關系（見表1）。所以高分組學生流程圖掌握程度好，在其支持下的計算思維就能夠得到更有效的提升。對于算法維度，由于前測時高分組得分已經達到較高水平，所以進步空間有限。

3. 對學生作品的分析

在本研究中，最終有12人完整地提交了3個項目的App作品。研究發現每個項目中流程圖得分高的學生其作品完成度更高，說明流程圖能夠幫助他們梳理思路、明確解決方案，減少直接編程帶來的盲目性。此外，隨著教學項目的逐步推進，越來越多的學生開始能夠在作品中體現個人想法，開發拓展功能。其中，83%位于流程圖高分組或流程圖得分提升幅度較大組（項目三之于項目一流程圖得分提升幅度位于前50%）。可見，流程圖掌握好的學習者更能夠自主發現情境中蘊含的問題，并能結合所學知識開發出解決該問題的功能，這也從側面展現了流程圖的引入能夠使學習者利用計算工具解決問題的能力增強，促進他們計算思維的發展。

（二）計算思維非認知層面的發展影響

在作品反饋問答中，有7名學生提出習得的問題解決思維和方法可以遷移用在日常的學習和生活中（圖3左上）。有2名學生明確表達課程發展了他們的邏輯思維能力，增強了他們學習數學等學科的興趣（圖3右上）。此外，還有7名學生認為在這樣的教學模式下，自身在解決問題的過程中更愿意堅持和探索;有8名同學表示，面對項目學習中遇到的困難他們不會立刻求助老師和同學，而是會優先選擇獨立思考，自主解決（圖3下）。在這些學生中，81%的人位于流程圖得分高分組或流程圖得分提升幅度較大組。這也進一步說明流程圖支持下的計算思維培養方式的有效性，通過體驗與習得解決問題的思維和方法，學習者的探索精神和自主意識有所增強。

（三）實踐中的問題探討

當然，研究中存在不少問題。比如，學生在項目二中的流程圖得分普遍偏低，一方面是因為項目二在三個項目中的算法難度相對最高，另一方面是因為沒有很好地考慮學生對流程圖繪制的適應過程。在學生正式熟悉流程圖應用之前，需要適當地加以引導，必要時可以給出部分支架讓學生以拼圖的形式去建構解決問題的方案。然后，隨著學生掌握程度的提高，再逐漸弱化這種引導和支持，以一種循序漸進的方式讓流程圖在教學中取得最好的效果。另外，研究發現7年級學生的流程圖得分相較于其他兩個年級偏低，7年級60%以上的學生位于流程圖得分低分組。進一步聯系實踐的課堂觀察分析原因，發現7年級的學生更傾向于動手操作，不愿在流程圖繪制上花時間，因此流程圖的完成度以及完成質量都普遍不高。6年級學生對教師的信任感較強，能夠按照課堂要求認真完成流程圖繪制任務;8年級學生自主性和自制力逐漸增強，對于有助于自身學習的方式方法能夠積極主動地貫徹實施;7年級學生在學習上處于一種被動與主動之間的臨界區域，缺乏持之以恒的態度，因而導致流程圖得分較低的現象。這在教學設計上帶給研究者的思考是，要注意提升流程圖繪制任務的趣味性以及問題粒度設置的適當性，以此吸引學生的注意力，讓他們主動投入繪制流程圖的環節。

四、總結與展望

人工智能的迅速崛起正在改變世界發展的態勢，而在K-12階段加快計算思維的培養是這一態勢競爭的重要一環。未來的世界需要能有效理解、應用并創造計算技術的人。我們需要具備主動而非被動地借助技術解決問題的思維和能力，這也將是未來人與人之間的重要區別（Thorson， 2018）。但在計算思維的常規培養模式下，教學過于關注程序的操作開發，強調思維的結果，而缺乏顯性化呈現解決問題的思維加工過程，很難深入思維發展的細節做出針對性的指導和評價，從而局限了計算思維培養的效果。在本研究中，流程圖作為一種思維發展承載工具被引入教學環節對實踐具有一定的指導意義。

新方式強調學習者解決每一個問題都伴隨著繪制流程圖，流程圖作為思維發聲的工具在識別問題、分解重構問題和形成方案的過程中發揮作用，幫助學習者梳理思路，記錄他們思維發展的全過程。研究初步證明了該方式能夠有效促進學習者計算思維中問題識別、問題分解、抽象、算法和邏輯等維度的發展，其中對流程圖得分高或得分提升幅度大的學習者的促進效果更加顯著。但該模式想要進一步推廣實踐還存在優化改進的空間。第一，為減輕學習者對流程圖使用的不適應性，教師在問題解決過程中應適當提供部分支架以輔助學習者完成流程圖繪制，幫助學習者減輕認知負荷。第二，教師要注意問題粒度設置的適當性和趣味性，以提高學習者完成任務的積極性和注意力集中度。此外，研究所采用的流程圖評價法、前后測測試法、作品評價法以及反饋問答題分析法等，全面呈現了學習者計算思維的認知和操作層面以及非認知層面的發展情況，能夠為實踐培養中的評價環節打開新思路。

作為21世紀的必備素養，K-12階段計算思維的培養與國家人才儲備與人才競爭息息相關，但目前這一研究仍處于發展階段（Freeman， et al.， 2017），需要從不同的視角、結合不同的手段加以支持和完善。但不管怎樣，只有將思維的形成與演變過程可視化，才能更好地引導和評價思維的發展。

[參考文獻]

龔靜，侯長林，張新婷. 2018. 計算思維能力發展模型與教學程序研究[J]. 現代教育技術，28（4）：48-54.

國務院. 2017-07-20. 新一代人工智能發展規劃[EB/OL]. [2018- 11-06]. http：//www.gov.cn/zhengce/content/2017-07/20/content_5211996.htm

教育部. 2018. 普通高中信息技術課程標準（2017年版）[M]. 北京： 人民教育出版社.

李鋒. 2018. 中小學計算思維教育：STEM課程的視角[J]. 中國遠程教育（2）：44-49，78-79.

劉濯源. 2014. 思維可視化：減負增效的新支點[J]. 中小學管理（6）：10-13.

王本陸，千京龍，盧億雷，等. 2018. 簡論中小學人工智能課程的建構[J]. 教育研究與實驗（4）：37-43.

王榮良. 2008. 機器人教育與工程思維關系之研究[J]. 中國教育信息化（24）：27-29.

王旭卿. 2014. 面向三維目標的國外中小學計算思維培養與評價研究[J]. 電化教育研究，35（7）：48-53.

楊超培. 1999. 程序化：一種重要的標準化方法[J]. 電子標準化與質量（1）：25-28.

郁曉華，肖敏，王美玲. 2018. 計算思維培養進行時：在K-12階段的實踐方法與評價[J]. 遠程教育雜志，36（2）：18-28.

趙慧臣，王玥. 2014. 我國思維可視化研究的回顧與展望：基于中國知網2003—2013年論文的分析[J]. 中國電化教育（4）：10-17.

Allan， W.， Coulter， B.， Denner， J.， Erickson， J.， Lee， I.， Malyn-Smith， J.， et al. （2010）. Computational thinking for youth. Retrieved November 12， 2018， from http：//stelar.edc.org/sites/stelar.edc.org/files/Computa tional_Thinking_paper.pdf

Atmatzidou， S.， & Demetriadis， S. （2016）. Advancing students computational thinking skills through educational robotics： A study on age and gender relevant differences. Robotics and Autonomous Systems， 75， 661-670.

Bocconi， S.， Chioccariello， A.， Dettori， G.， Ferrari， A.， & Engelhardt， K. （2016）. Developing computational thinking in compulsory education-Implications for policy and practice. Retrieved November 12， 2018， from http：//publications.jrc.ec.europa.eu/repository/bitstream/JRC104188/jrc104188_computhinkreport.pdf

Brennan， K.， & Resnick， M. （2012， April）. New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 annual meeting of the American Educational Research Association， Vancouver， Canada （Vol. 1， p. 25）.

Chen， W.， Li， Z.， Bao， A.， & Tang， Y. （2015， November）. Curriculum design for computational thinking training based on concept map. In 2015 7th International Conference on Information Technology in Medicine and Education （ITME） （pp. 413-416）. IEEE.

Chen， G.， Shen， J.， Barth-Cohen， L.， Jiang， S.， Huang， X.， & Eltoukhy， M. （2017）. Assessing elementary students computational thinking in everyday reasoning and robotics programming. Computers & Education， 109， 162-175.

Crews， T.， & Ziegler， U. （1998， November）. The flowchart interpreter for introductory programming courses. In FIE98. 28th Annual Frontiers in Education Conference. Moving from ‘Teacher-Centered to ‘Learner-Centered Education. Conference Proceedings （Cat. No. 98CH36214） （Vol. 1， pp. 307-312）. IEEE.

CSTA & ISTE. （2011）. Operational definition of computational thinking for K-12 education. Retrieved November 12， 2018， from http：//www.iste.org/docs/pdfs/Operational-Definition-of-Computational-Thinking.pdf

DeCaprio， S. A. （1981）. Flowcharting： A method of problem solving. Retrieved November 12， 2018， from http：//teachersinstitute.yale.edu/curriculum/units/1981/6/81.06.03.x.html

Freeman， A.， Adams Becker， S.， Cummins， M.， Davis， A.， & Hall Giesinger， C. （2017）. NMC/CoSN Horizon Report： 2017 K-12 Edition. Retrieved November 12， 2018， from https：//cdn.nmc.org/media/2017-nmc-cosn-horizon-report-k12-EN.pdf

Gouws， L. A.， Bradshaw， K.， & Wentworth， P. （2013， July）. Computational thinking in educational activities： An evaluation of the educational game light-bot. In Proceedings of the 18th ACM conference on innovation and technology in computer science education （pp. 10-15）. ACM.

Grover， S.， & Pea， R. （2013）. Computational thinking in K-12： A review of the state of the field. Educational Researcher， 42（1）， 38-43.

Hooshyar， D. A. N. I. A. L.， Ahmad， R. B.， Shamshirband， S.， Yousefi， M.， & Horng， S. J. （2015）. A flowchart-based programming environment for improving problem solving skills of Cs minors in computer programming. The Asian International Journal of Life Sciences， 24（2）， 629-646.

Hu， M. （2003， July）. A case study in teaching adult students computer programming. In Proceedings of the 16th Annual NACCQ （Vol. 287）.

Izu， C.， & Weerasinghe， A. （2014）. Flowcharts： A tool for computational thinking. Conference Proceedings of the Australian Computers in Education Conference 2014. Australia， 305-313.

Korkmaz， ?.， ?akir， R.， & ?zden， M. Y. （2017）. A validity and reliability study of the computational thinking scales （CTS）. Computers in Human Behavior， 72， 558-569.

Massachusetts Department of Education （2006， October）. Massachusetts science and technology/engineering curriculum framework. Retrieved November 12， 2018， from https：//files.eric.ed.gov/fulltext/ED508413.pdf

Powers， K.， Gross， P.， Cooper， S.， McNally， M.， Goldman， K. J.， Proulx， V.， et al. （2006， March）. Tools for teaching introductory programming： What works？ In ACM SIGCSE Bulletin （Vol. 38， No. 1， pp. 560-561）. ACM.

Repenning， A.， Basawapatna， A.， & Escherle， N. （2016， September）. Computational thinking tools. In 2016 IEEE Symposium on Visual Languages and Human-Centric Computing （VL/HCC） （pp. 218-222）. IEEE.

Román-González， M.， Pérez-González， J. C.， & Jiménez-Fernández， C. （2017）. Which cognitive abilities underlie computational thinking？ Criterion validity of the Computational Thinking Test. Computers in Human Behavior， 72， 678-691.

Selby， C. C.， & Woollard， J. （2013）. Computational thinking： The developing definition. Retrieved November 12， 2018， from https：//eprints.soton.ac.uk/356481/1/Selby_Woollard_bg_soton_eprints.pdf

Snow， E.， Tate， C.， Rutstein， D.， & Bienkowski， M. （2017）. Assessment design patterns for computational thinking practices in exploring computer science. Retrieved November 12， 2018， from https：//pact.sri.com/downloads/AssessmentDesignPatternsforComputationalThinking%20PracticesinECS.pdf

Sullivan， A. A.， Bers， M. U.， & Mihm， C. （2017）. Imagining， playing， and coding with KIBO： Using robotics to foster computational thinking in young children. Siu-cheung KONG The Education University of Hong Kong， Hong Kong， 110-115.

Thorson， K. （2018， March 18）. Early learning strategies for developing computational thinking skills. Retrieved November 12， 2018， from https：//www.gettingsmart.com/2018/03/early-learning-strategies-for- developing-computational-thinking-skills/

Wang， D.， Wang， T.， & Liu， Z. （2014， February 25）. A tangible programming tool for children to cultivate computational thinking. The Scientific World Journal， 2014， Article 428080. Retrieved November 12， 2018， from https：//www.hindawi.com/journals/tswj/2014/428080/

Wing， J. M. （2006）. Computational thinking. Communications of the ACM， 49（3）， 33-35.

收稿日期：2019-01-15

定稿日期：2019-07-02

作者簡介：郁曉華，博士，副教授，碩士生導師;王美玲，碩士研究生。華東師范大學教育學部教育信息技術學系（200062）。

責任編輯 單 玲