嫦娥四號著陸器月面定時定點著陸軌道控制策略設計與實施

劉德成 周文艷 高珊 李飛 楊眉

(北京空間飛行器總體設計部，北京 100094)

嫦娥三號探測器的目標著陸區為虹灣地區，整個區域面積廣大，地勢均較為平坦，因此可以選一個面積較大的預定著陸區域，對于不同的發射日期和轉移軌道，即便存在一定的軌道飛行控制誤差，總可以找到滿足任務要求的著陸點，因此沒有定點著陸的需求。嫦娥四號探測器任務目標為著陸月球背面。相對于月球正面，背面地形更加崎嶇復雜，大量的撞擊盆地密布，難以找到大片的平坦區域，由此提出了定點著陸的要求[1-3]。另一方面，動力下降前的測控弧段也是必須保證的條件，而測控弧段與著陸時刻直接相關，因此又對嫦娥四號著陸器提出了定時著陸的要求。

根據著陸任務的飛行過程，定點著陸常用的變軌策略主要是圈次調整、調相軌道和軌道面調整等[4-6]。文獻[7]以月面定點采樣返回任務為背景，根據采樣返回任務的飛行時序和測控條件約束分析了月球傾斜軌道的定點采樣變軌策略，采用一個2對2的機動瞄準目標動力下降起始點高度和著陸點緯度，通過軌道平面調整機動瞄準目標著陸點緯度，但該策略未對著陸點時刻進行約束。本文根據嫦娥四號的任務約束，在考慮測控要求、環月傾角接近90°的條件下，以滿足嫦娥四號任務需求為目標，提出了一種基于雙層迭代的高精度“定時定點”月面軟著陸軌道控制策略，然后針對飛控中各種因素的殘差，在近月制動和環月修正增加面外修正速度增量，確保落點位置和時刻的精度滿足要求。

1 單層迭代的軌道控制策略

嫦娥三號軟著陸任務的著陸區為月球正面的虹灣，由于虹灣地區相對而言較為平坦，可著陸區域較大，任務計劃的著陸區域為：月面緯度44.1°N±1.5°N，經度18.2°W～34.6°W。

著陸區域經度方向范圍寬達16.3°，月球每天自轉13.2°，因此對于傾角為90°的環月軌道，通過調整環月飛行時間即可保證探測器落在指定區域內，對于著陸器并不存在定時定點著陸的要求。

嫦娥三號的飛行過程以及軌道控制策略如圖1所示，整個飛行過程由地月轉移段、環月飛行段和動力下降段組成。嫦娥四號著陸器的主要飛行過程與嫦娥三號類似[8]。本文不考慮動力下降段誤差對著陸點的影響，重點闡述的是通過對地月轉移段和環月飛行段的軌道控制策略設計，使得著陸器在動力下降初始點預報的著陸點滿足任務要求。

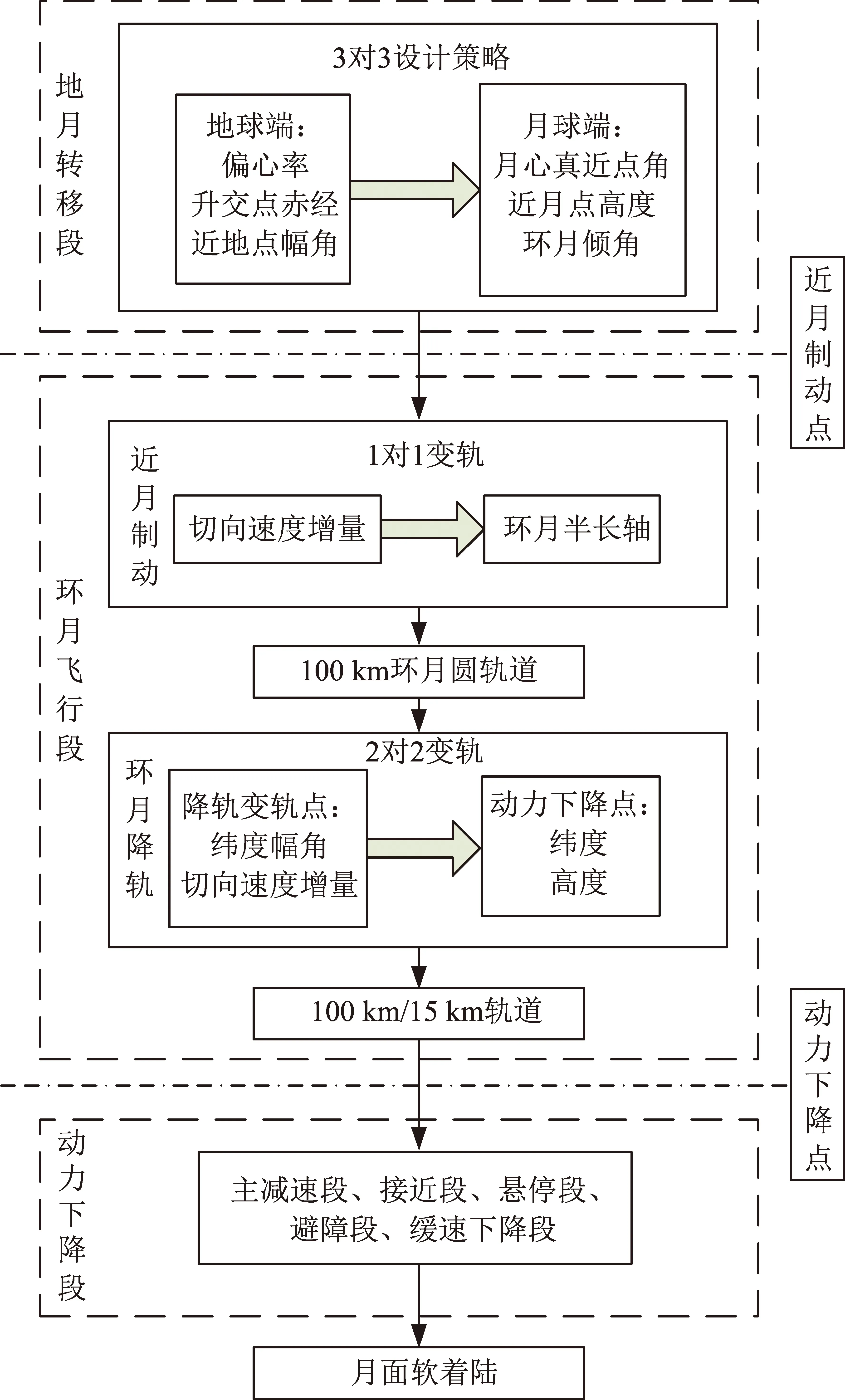
圖1 嫦娥三號探測器飛行過程及軌道控制策略

圖1中，“3對3設計策略”、“1對1變軌”中前面的數字為設計變量的個數，后面的數字為目標變量的個數，采用微分修正方法迭代設計變量滿足目標變量的要求，令q為目標變量，p為設計變量，則目標變量和設計變量之間的關系可以表示為[9]

q=q(p)

(1)

猜測一個初值p0，則q0=q(p0)，得到Δq=qT-q0，其中qT為目標值。

兩者之間的誤差關系可線性化表示為

(2)

p=p0+Δp

(3)

通過若干次迭代，就可以使得Δq滿足允許誤差，這是求解微分方程常用的方法。

在地月轉移段中

(4)

(5)

式中：v0為近地點速度；Ω為升交點赤經；ω為近地點角距；Hm為近月點高度；k為月心赤道慣性坐標系z軸方向的單位矢量；r1，v1是月心慣性系中近月點的位置與速度。由q2和q3的表達式可知：q2表示探測器在近月點時相對于月球的速度和月心矢徑的夾角的余弦，q3表示探測器在近月點時相對于月球赤道面的瞬時軌道傾角。

在近月制動時

(6)

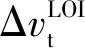
在環月降軌時

(7)

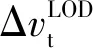
根據圖1的軌道方案進行計算，各發射窗口標稱軌道參數如表1所示。

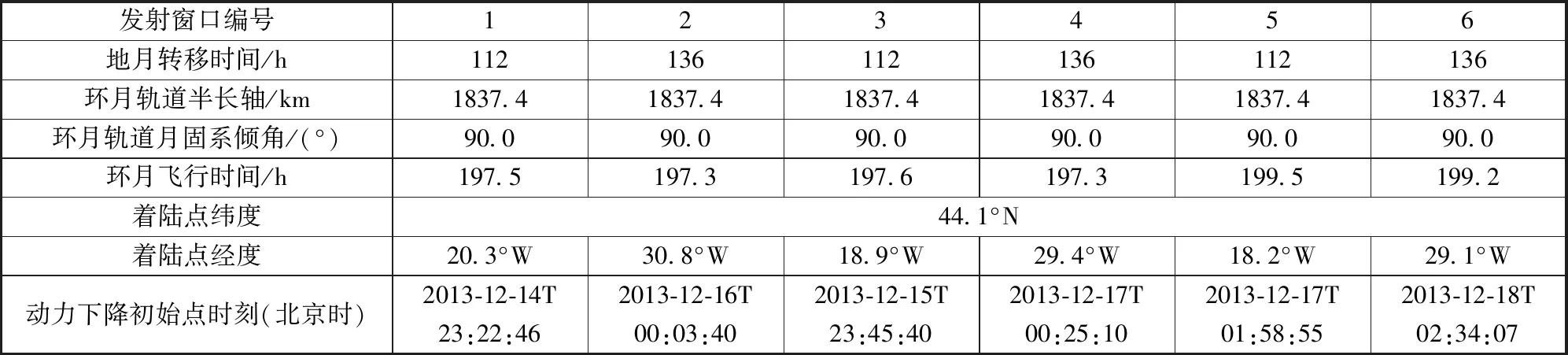
表1 嫦娥三號探測器標稱軌道參數

由以上結果可知，每一個發射窗口的標稱環月軌道半長軸和傾角相同，但動力下降初始點時刻及對應的標稱落點各不相同，112 h轉移時間軌道的標稱落點集中在20°W附近，136 h轉移時間軌道的標稱落點集中在30°W附近。

2 雙層迭代定時定點著陸軌道控制策略

嫦娥四號預定主著陸區為月面經度177.6°E±1.2°E，月面緯度45.5°S±0.5°S，著陸范圍僅有嫦娥三號著陸區范圍的5%，圖2等比例給出了嫦娥三號與嫦娥四號著陸的目標著陸區。

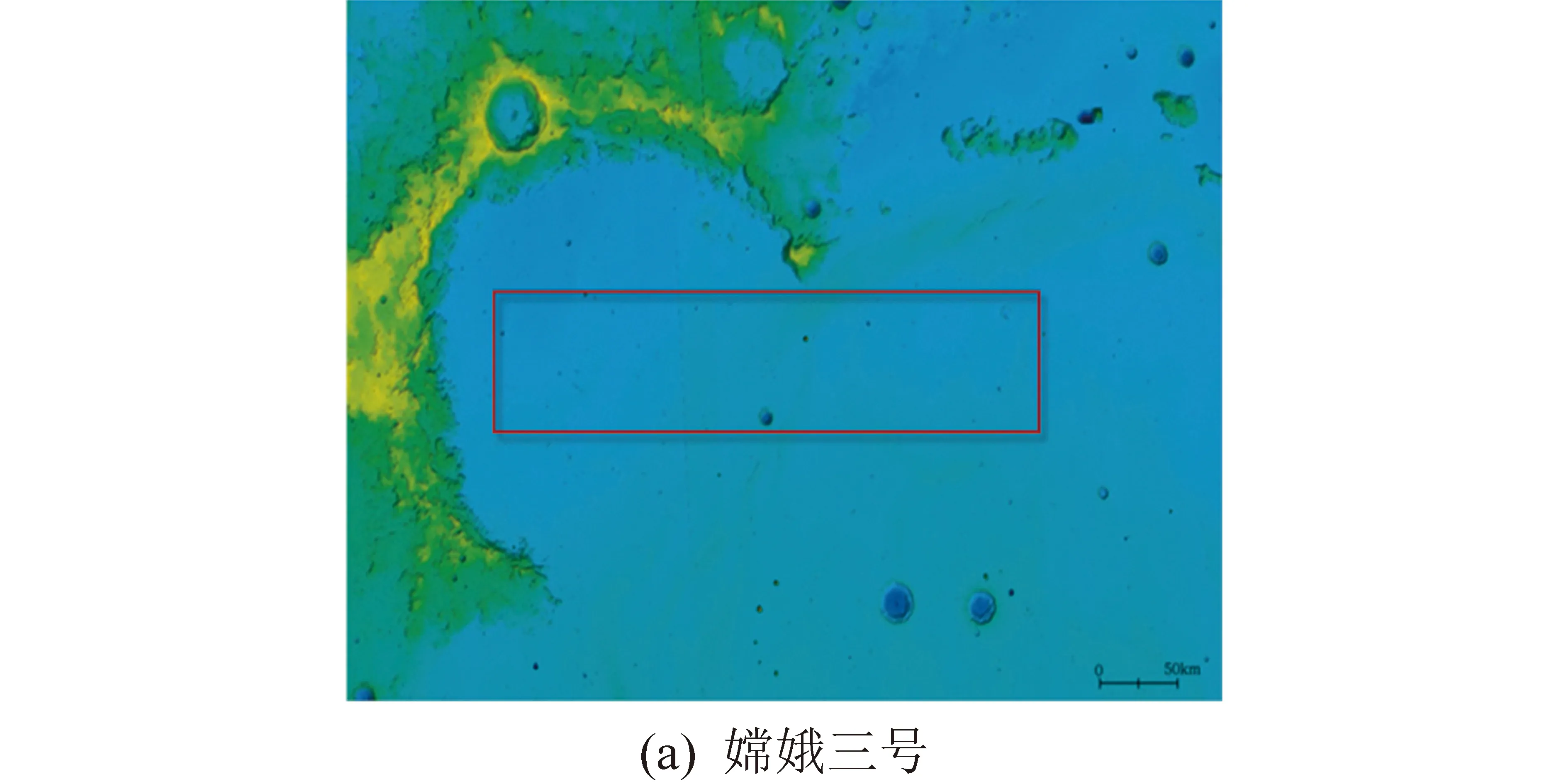
圖2 嫦娥三號與嫦娥四號目標著陸區域

受動力下降段GNC系統制導律的約束，著陸器在動力下降段不具備著陸點位置的調整能力，因此動力下降初始點(自由飛行軌道與動力下降段的銜接點)的位置才是決定著陸點位置的重要因素。考慮到著陸器動力下降過程存在著陸點誤差，并留取一定余量，因此任務要求軌道控制殘差帶來的落點經度(落點緯度誤差通過微調動力下降點時刻保證)精度要求小于0.1°；地面測控站對著陸器的可見性又限定了著陸時刻，任務中要求著陸時刻誤差小于1 min。針對這一問題，設計了一種基于雙層迭代的高精度“定時定點”月面軟著陸軌道控制策略，通過近月制動和環月修正多次應用該軌道控制策略，逐次縮小軌道控制殘差，滿足著陸區范圍縮小帶來的動力下降初始點的位置和時刻精確瞄準的需求。

該軌道控制策略主要包括兩層迭代(流程如圖3所示)：①外層迭代為“2對2”的軌道控制策略，設計變量為環月變軌(包括近月制動和環月修正)速度增量的切向和法向控制量，目標為動力下降初始點時刻與著陸點經度；②內層迭代包含另一個“2對2”的軌道控制策略，設計變量為環月降軌時刻及變軌速度增量，目標為動力下降點高度和緯度。

在實際飛控實施中，當已完成近月制動和環月修正，需要進行環月降軌策略計算時，增加環月降軌變軌速度增量法向控制量為設計變量來瞄準著陸點經度，形成“3對3”的軌道控制策略，即設計變量為環月降軌時刻、變軌速度增量切向和法向控制量，控制目標為動力下降點高度、緯度和著陸點經度。

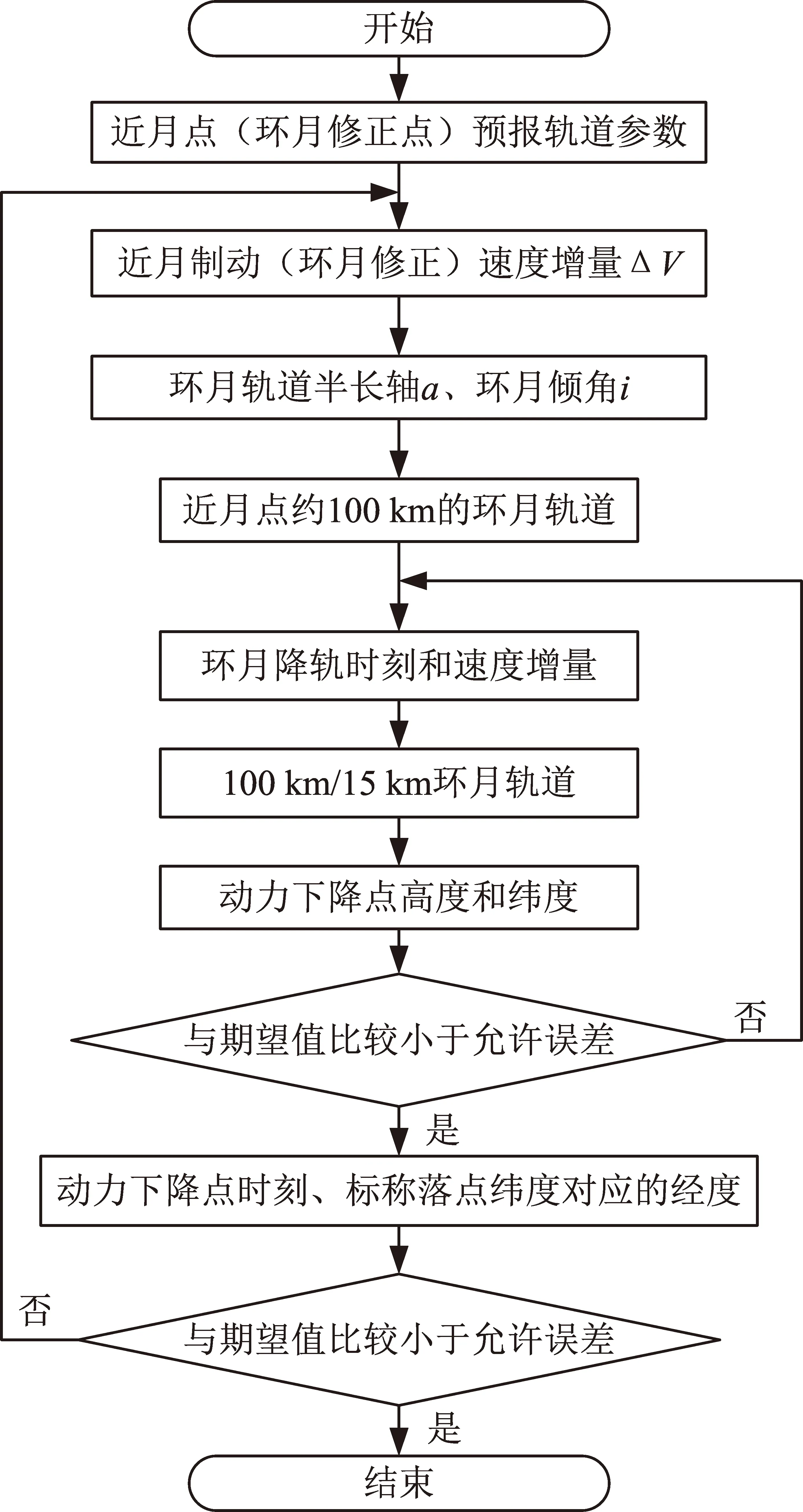
圖3 嫦娥四號著陸器雙層迭代軌道控制策略

雙層迭代的軌道控制策略計算流程如下：

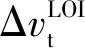
對于近月制動

(8)

(2)得到近月變軌量后，疊加到近月點制動前的軌道狀態，預報至環月降軌點，進入第二個內層迭代，目標變量為動力下降初始點(同時也是此時環月軌道的近月點)高度和緯度，設計變量為環月降軌點緯度幅角和切向軌道控制速度分量，當動力下降初始點高度和緯度值與目標值誤差滿足允許誤差，結束計算。

(9)

(3)得到環月降軌變軌量后，疊加到環月降軌前的軌道狀態，將軌道預報至動力下降初始點，得到動力下降初始點緯度φd、軌道傾角im、動力下降航程L和動力下降飛行時間Td，計算月面著陸點經緯度(λL、φL)和著陸時刻TL。

由動力下降航程L，動力下降緯度φd和傾角im計算落點緯度φL過程如圖4所示。

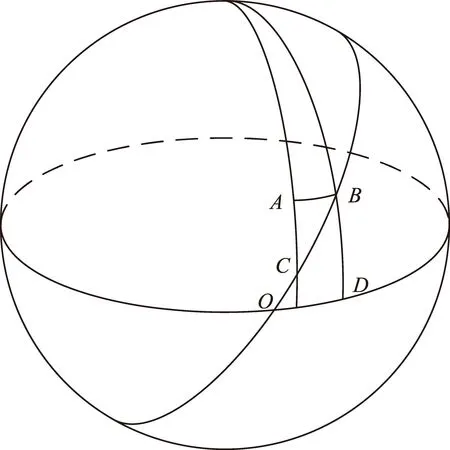
圖4 動力下降段幾何示意圖

(10)

對應升軌

(11)

對應降軌

(12)

式中：Rm為月球參考半徑，一般取1 737.4 km。

則落點緯度φL為

(13)

由落點緯度φL和傾角i計算落點經度λL為

對應升軌

(14)

對應降軌

(15)

式中：ωm為月球自轉角速度，一般取2.661 7×10-6rad/s。

(4)計算得到月面著陸點經緯度(λL、φL)和著陸時刻TL后，進入外層迭代，目標變量為著陸點時刻、著陸點經度，設計變量為環月半長軸am和軌道傾角im。

(16)

當月面著陸點經緯度和著陸時刻與目標值誤差滿足允許誤差，結束計算，進入計算步驟(1)。

(5)在近月制動完成后，以近月制動軌道控制后定軌參數替代近月制動前定軌參數，按步驟(1)～(4)計算環月修正軌道控制速度增量大小和方向。

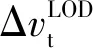
(17)

當目標變量與目標值誤差滿足允許誤差，結束計算。

使用以上策略設計標稱軌道，得到的標稱軌道參數如表2所示。

由表2可知，嫦娥四號探測器每一個發射窗口的標稱環月軌道半長軸和傾角不相同，但對應的標稱落點和動力下降點時刻均相同，實現了理論上的定時定點著陸。

3 軌道控制策略實施

使用雙層迭代軌道控制策略設計標稱軌道，使得不同的發射窗口均可實現的定時定點著陸，但在實際飛控由于定軌、軌道預報和軌道控制執行等均存在誤差[10]，需要在近月制動、環月修正和環月降軌時加入法向修正，相應的變軌策略則變由“2對2”變成“3對3”，這樣通過雙層迭代策略的多次應用，使得動力下降初始點預報的落點經度誤差滿足任務要求。

在飛控實施的過程中，環月段月球引力場采用100×100的高精度模型，由于環月時間較長，考慮兼顧計算效率和執行精度，將地月轉移段和環月段解耦，地月轉移段的中途修正瞄準標稱的近月點高度和環月軌道傾角，從使近月制動開始，每次變軌同時使用面內面外變軌以確保定時定點的著陸任務要求，飛控過程中從近月制動到環月降軌歷次軌道機動執行的軌道控制量的法向修正量如表3所示。

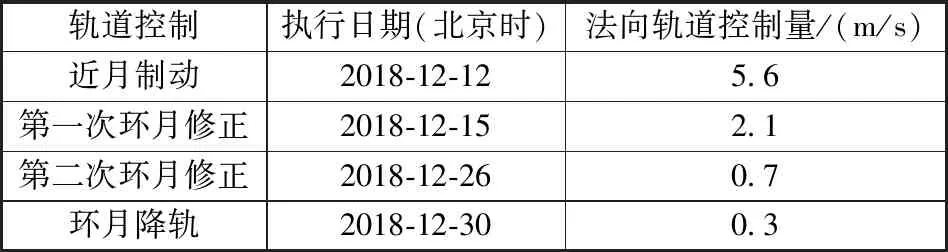
表3 飛控實施軌道控制策略的法向修正量

從飛控中法向軌道控制量的實施結果來看，控制量越來越小，這表明通過多次應用雙層迭代的軌道控制策略，逐次減小了軌道控制殘差，最終根據動力下降初始點定軌參數預報的落點經度差僅為0.004°，落點時刻預報誤差小于25 s，完全滿足任務要求。

4 結束語

在嫦娥三號軌道控制策略的基礎上，針對嫦娥四號任務目標，在考慮測控條件、環月傾角接近90°的條件約束下，在標稱軌道設計時，利用雙層迭代的高精度“定時定點”月面軟著陸軌道控制策略，使得不同的發射窗口實現理論上的月面定時定點著陸；然后在飛控實施階段，在近月制動、環月修正和環月降軌等軌道控制同時進行切向和法向軌道控制，多次應用該策略，可減小軌道控制殘差，獲得的動力下降初始點定軌參數對應理論月面落點經度誤差僅為0.004°，落點時刻預報誤差小于25 s，為實現月面定時定點著陸提供了良好的初始條件。若在該軌道控制策略的基礎上，動力下降段制導律具備一定的針對確定落點的調整能力，則可實現完全的月面定時定點著陸，這在我國將來的建立永久月球基地等月球后續探測任務中具有重要應用價值。