超高維判別分析中的迭代穩健特征篩選方法

何勝美

（廣東金融學院 金融數學與統計學院，廣東廣州510521）

隨著科學技術的發展，大數據成了當下研究的熱點.高維作為大數據的主要特征，得到了學者們的廣泛關注.在數據分析中，當特征的維數超過樣本量，統計建模分析將面臨巨大的挑戰.對于高維數據，涌現出來一批傾向于精確變量選擇的方法，例如 LASSO［1］，SCAD［2］，Elastic net［3］以及它們的各種擴展［4-5］.但是，超高維時，上述變量選擇方法在計算成本，統計的準確性以及算法的穩定性上都遇到巨大挑戰.Fan和Lv在線性模型假情況下，利用邊際皮爾森相關性對協變量做初步篩選，提出了確定性獨立篩選方法（SIS），證明在一定條件下該方法滿足確定篩選性質，即模型所選變量集合包含全部真實變量的概率趨近于1，首次提出了變量篩選的概念［6］.隨之而來，各種以邊際效用為基礎的變量篩選方法相繼涌現.比如線性與廣義線性模型上有基于最大邊際似然的篩選方法［7］和基于邊際經驗似然比的變量篩選方法［8］.非參數方法上有Fan等的基于b樣條估計邊際相關效用的非參數獨立篩選［9］、NIS，Li等的基于Kendall相關的變量篩選方法［10］、距離相關篩選方法［11］、球相關變量篩選方法［12］等.針對超高維判別分類問題，也有相關變量篩選方法出現，例如Ma 和 Zou 的 Kolmogorov filter（KF）［13］；Cui等的適用于多分類的穩健特征篩選方法 MV-SIS［14］及其修正方法 AD-SIS［15］.

邊際思想讓變量篩選方法能夠對超高維模型進行快速降維，但是它忽略了變量間可能存在的強相關性，進而導致漏選重要變量或者錯選不重要的變量.為解決這個問題，很多方法都提出了相應的迭代篩選形式，例如 ISIS［6］，ISIRS［16］，DC-ISIS［17］，MBKR-ISIS［18］和 QC-ISIS［19］，但上述這些方法主要針對連續變量問題，對于超高維分類問題的變量篩選，相應的迭代篩選還沒有得到充分的研究.

本文在Cui等人提出的MV-SIS［14］和He等人提出的AD-SIS［15］的研究基礎上，考慮超高維分類數據的判別分析的迭代變量篩選問題.結合Zhu等的思想［16］，提出了超高維判別分類問題中的迭代特征篩選方法MV-ISIS和AD-ISIS，并通過數值模擬，研究了這兩種方法的有限樣本效果.

1 迭代特征篩選方法

1.1 MV-SIS和AD-SIS

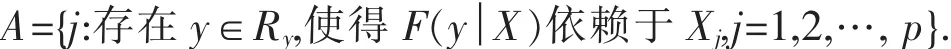
這里 F（y│X），是給定 X 的條件下 Y 的分布函數.則若 j∈A，Xj為重要變量，反之，若 j?A，Xj為不重要變量.令F(x)=Pr(X≤x)是隨機變量X的分布函數，Fr(x)=Pr(X≤x|Y=yr)是給定Y=yr的條件下，X的條件分布函數，以及pr=P(Y=yr)，Cui等人提出了：

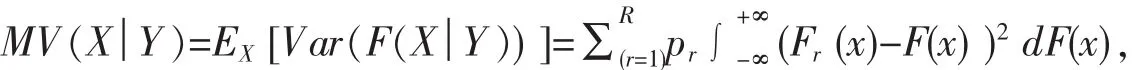
來刻畫X與Y的依賴性［14］.顯然，MV（X│Y）=0當且僅當X與Y相互獨立.因此MV（X│Y）可以作為變量篩選指標.給定n個獨立同分布的樣本{(Xi,Yi),i=1,2,…,n}，Cui等提出了適用于超高維判別分析的變量篩選方法 MV-SIS［14］來求如下特征集合：

其中，d=［n/log(n)］，ω?k是第 k個變量相應指標的樣本估計，其具體計算如下：

對于厚尾數據，MV-SIS并不能很好反映條件分布函數與無條件分布函數在尾部的差異，He等通過引進權重函數φ(F(x))=1/F(x)(1-F(x))對MV-SIS進行修正，得到：

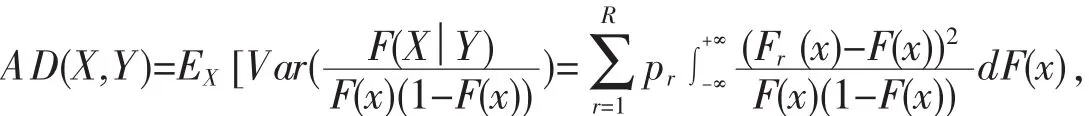
以及：

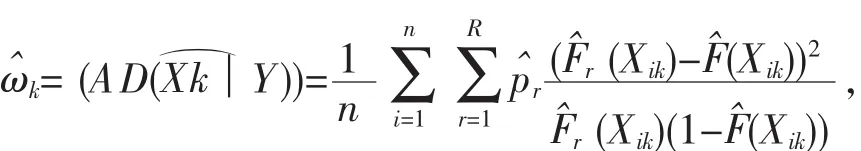
以此得到新的適用于判別分析的超高維特征篩選方法AD-SIS［15］.

1.2 迭代特征篩選MV-ISIS和AD-ISIS

MV-SIS和AD-SIS在數值模擬研究和實際數據研究中都顯示了不錯效果.但是，二者都是基于某一邊際效應指標的特征篩選方法，忽略了變量間可能存在的強相關性，進而可能導致漏選重要變量或者錯選不重要的變量.類似于Zhu等的思想［16］，本文基于MV-SIS（AD-SIS）做如下迭代算法：

第一步，應用變量篩選方法MV-SIS(或者AD-SIS)對觀測樣本(X,Y)進行篩選，記這一步中篩選的變量.

第二步，記 X1=(X1A1,X2A1,…,XnA1)，顯然，X1是是 n×(p-|A1|)矩陣.然后，進一步利用 MV-SIS(或者 AD-SIS)對新數據(Xnew,Y)進行變量篩選，篩選出另外d2個特征，記為

第三步，更新A1=A1∪A2和d1=d1+d2，再重復第二步，直到篩選的變量達到預先給定的數量.最終篩選的變量集合設為A1，則變量數量為d=|A1|.

上述迭代篩選方法簡記為MV-ISIS和AD-ISIS.其中，通常設定d=[n/log(n)]，實際模擬中選擇d1=d2=5.另外，注意到與 Xnew不相關，因此，MV-ISIS(或者AD-ISIS)能在一定程度上解決變量間可能存在的強相關導致的漏選重要變量或者錯選不重要的變量的問題.

2 數值模擬

下面通過蒙特卡羅模擬來評價迭代篩選算法MV-ISIS和AD-ISIS的效果.

例1 考慮其中，預測變量生成于正態分布 N(0p,Σ)的隨機向量，0p是 p 維零向量，Σ=(σij)p×p為協方差矩陣，滿足：（1）σij=1，i=1,2,…,i≠4；（3）σij=ρ，i≠j，j≠4 和 i≠4.ε 為誤差項.按照下列規則離散化得到 Y：

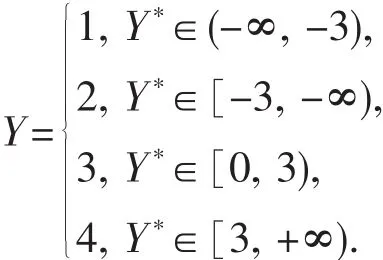
顯然，該模型中，Y依賴于X1,X2,X3和X4，但是不難計算Cov(Y*,X4)=Cov(5X1+5X2+5X3-155Cov(X1,X4)+5Cov(X2,X4)+5Cov(X3,X4)-15=0.因此，Y*與X4是邊際獨立的，從而 Y 與 X4也是邊際獨立的.取 n=200，p=2 000，考慮以下情況：（1）ρ=0.5 和 0.8；（2）ε～N(0,1)和 ε～t(1).

分別利用MV-SIS，AD-SIS，MV-ISIS和AD-ISIS對生成的數據進行變量篩選，比較它們變量篩選的效果.通過500次獨立重復模擬，統計變量Xi正確篩選的頻率pi，i=1,2,3,4,同時4個變量同時正確篩選的頻率pa，結果如表1和表2所示.

表1 例1中誤差項 ε～N（0，1）情形下模擬數據變量篩選結果

表2 例1中誤差項ε～t（1）情形下模擬數據變量篩選結果

表1和表2結果表明，MV-SIS和AD-SIS的變量篩選結果受到變量間的相關性影響較大，當變量間相關系數由0.5增長到0.8時，變量X1，X2和X3被正確篩選的頻率有較大的下滑（無論誤差項是標準正態情形還是t(1)分布情形）.而迭代篩選算法有效的解決了上述問題，尤其是對于p=0.8高相關的情況，MV-ISIS（AD-ISIS）大幅度提高了變量X1、X2和X3被正確篩選的頻率.例如在表2中，當p=0.8時，MV-SIS和ADSIS對第一個變量篩選的概率p1只有0.690和0.712，但迭代方法的結果有了較大提升，MV-ISIS和AD-ISIS均為為0.998，其它情況也都有類似的結果.而對于X4的篩選，由于X4與類別變量Y邊際獨立，MV-SIS和AD-SIS在各種情況下都未能正確的將X4篩選出來，相應的概率p4都為零，從而導致4個變量全部被正確篩選的概率pa全為零.而兩種迭代篩選方法得到了滿意的結果.表2結果顯示，在誤差項，ε～t(1),p=0.8時，MV-ISIS和AD-ISIS對應的p4分別從零上升到了0.864和0.918，相應的pa也從零分別提高到了0.864和0.918.

3 結語

本文研究了超高維判別分類問題中的迭代變量篩選問題，針對以往邊際篩選方法忽略了變量間可能存在的強相關性，進而可能導致漏選重要變量或者錯選不重要的變量的問題，提出了兩種迭代穩健變量篩選方法MV-ISIS和AD-ISIS，并通過數值模擬，討論了這兩種方法在有限樣本上的效果.模擬結果表明，在判別分類模型中，某些不重要變量與重要變量高度相關，而其他重要變量與類別變量的相關性較弱；或者某些變量與類別變量邊際相關性較弱，但聯合相關性又較強時，MV-ISIS（或者AD-ISIS）能大幅提高原始方法MV-SIS（AD-SIS）的變量篩選效果.