方格網法土（石）方計算的參數選擇與誤差分析

趙治華

摘要：本文分析了目前流行的方格網法計算土（石）方開挖回填計算時，如何選擇計算參數與地形特征要素，并通過各種參數和地形特征要素之間的誤差分析與對比，從而確定在不同地形特征要素情況下合理、正確的參數選擇，以提高土（石）方計算的精度。

關鍵詞：方格網法;計算參數;誤差分析

在數字化測圖非常普及的時代，作為場地平整土（石）方計算的首選方法——方格網法，以它簡便直觀，易于操作的特點，深受廣大技術工作者的青睞，因此這一方法在實際工作中應用非常廣泛。方格網間隔計算參數可以是5m、10m和20m，也可以是任意值，但在實際的計算中一般多采用10m×10m的方格網。而方格網間隔到底存在多大的誤差，誤差的主要來源在哪里，如何降低計算誤差，目前沒有明確的規范與要求來統一這個技術范疇的參數。由原理可知，方格的寬度越小，計算精度越高。但如果給定的格網間隔的值太小，超過了野外采集的點的密度也是沒有實際意義;如果給定的格網間隔的值太大，就會出現計算誤差的增加。如何合理、正確地計算出結果，就顯得尤為重要。

一般工程在“三通一平”的階段地形圖的比例尺為1∶500和1∶1000兩種，本文均以比例尺為1∶500地形圖為例。在《1∶500_1∶1000_1∶2000外業數字測圖技術規程》中規定，比例尺為1∶500地形圖的地形點平均間距25m，在地形圖整飾

階段，為美觀起見，地形點離散后的間隔也就在20m左右，就作為正式圖紙成果發布提交了。

1.土（石）方計算參數的分析

1.1CASS9.1的方格網計算原理

該軟件的方格網計算土（石）方量是根據實地測定的地面點坐標（X，Y，Z）和設計高程，通過生成方格網來計算每一個方格內的填挖方量，最后累計得到指定范圍內填方和挖方的土（石）方量，并繪出填挖方分界線。程序系統首先將方格的四個角上的高程相加（如果角上沒有高程點，通過周圍高程點內插得出其高程），取平均值與設計高程相減。然后通過指定的方格邊長得到每個方格的面積，再用長方體的體積計算公式得到填挖方量。

由此可見，地形點的高程值是計算土（石）方的關鍵參數，并由其疏密程度決定方格網的間隔值。

在山區地貌特征的數字化的地形圖中，等高線就可以作為高程點加密的首選要素。在地形點稀疏的地形圖中，一般地形點的平均間隔在25m左右，理論上只能計算方格網間隔值20m以上的土（石）方量，相對計算結果誤差較小或比較合理、正確，而采用10m方格網間隔值來計算土（石）方量，顯然是存在誤差或不合理性的。

在CASS9.1軟件中有一個等高線生成高程點的功能，如左圖。利用這個功能，生成相對密集的高程點，就可以彌補高程點不足的缺陷。但前提是：等高線的屬性一定要正確，因為等高線繪制的屬性在非專業看來也就是一條曲線，但這一功能在還原地形點上是不能存在錯誤的。錯誤的屬性，必然帶來錯誤的結果，只有正確的結果，才能實現較小方格網值的土（石）方計算過程，并且把計算誤差降低到最小。

在外業測量過程中，許多地形點沒有刪除的必要。不應該因為美觀，而離散地形點，這樣會喪失掉數字化地形圖本身其他計算的精度要素。數字化圖的判讀和直接利用

（DTM數字模型的建立）是兩個概念。以某工程的土（石）方計算為例就很直觀看出計算誤差的存在。

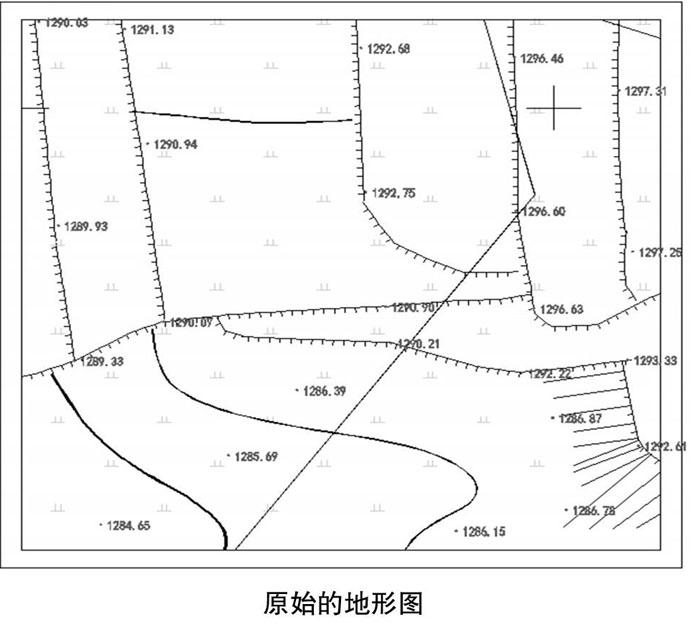
下圖為原始的地形圖，地形高程點的疏密程度在10m～20m之間，滿足《1∶500_1∶1000_1∶2000外業數字測圖技術規程》中規定。

從上述計算結果來分析，格網間隔值越小，計算的填挖方量越大，這也是乙方施工單位追求的理想結果，而甲方業主單位則反之。這其中存在很大的系統誤差，或者說人為因素。但如何準確地計算出實際量，就需要如實地進行地形特征要素的加密與取舍，真實地建立DTM數據結構模型，才能得到較為真實的結果。這也正是許多工程技術人員忽略的地方。

2.地形特征要素取舍的原則分析

在實際的測量數據還原原地形地貌特征點時，也就是形成DTM數字模型時，往往需要加密地形點，才能真實的反映出真實的地貌特征。下圖為原始數據形成的DTM模型圖。

從這張圖上，我們明顯地看出跟實際的地貌特征出入較大，而大家往往根據這個DTM數據模型在計算土（石）方量，即便是土（石）方計算的間隔再小，得出的土（石）方計算結論也存在較大的誤差。要準確地建立DTM數據模型，就得進行地形點的加密工作。

加密地形點的位置一般在：A.陡坎的頂底位置;B.坡面的頂底位置;C.計算范圍的邊緣地帶;D.其他地形變化的交界地帶等。

加密地形點一般采用內插法進行。加密地形點不必顧忌地形圖的整體美觀性，要以DTM數字模型和實際地貌特征反復比對，直到符合客觀實際為止。

下圖為加密地形點后的地形圖和加密地形點后的DTM數據模型。

從上述計算結果來分析，在地形點加密處理后，格網間隔值的大小，不再是決定計算填挖方量的決定因素，更在一定程度上體現出準確、公平、公正和合理。系統誤差或者說人為因素在很大程度上得以解決。這才是作為一名工程技術人員需要把握的根本。

3.土石方計算的誤差值的確定

如何確定土（石）方計算的誤差，首要的因素是確定真值。就土（石）方計算而言，在地形點加密處理后，用三角網法計算的結果最接近真值。就本例而言三角網法的計算結果如下：

在確定了真值以后我們進行土（石）方計算的誤差分析，土（石）方計算的誤差分析表就是分析比照表。

從土（石）方計算的誤差分析表可以看出，在土（石）方計算中，雖然沒有較為明確的計算參數可選擇，但從準確、合理、公正的立場出發，在土（石）方計算時，必須進行地形點的加密處理，在此基礎上方可進行計算方法的選擇。計算方法不是決定計算誤差的主要因素，地形點的稀疏周密，才是根本上反映地貌特征的決定因素，也是決定計算準確性的唯一客觀依據，這一點在山區不規則地形中，顯得尤為重要。

在實際工程現場中，一般將土（石）方計算誤差控制在5%～10%的范圍內，認為是較為合理的，但也不能把計算誤差看成土（石）方計算的參考值，隨著土（石）方量的加大，計算誤差理論上應該是越小的。就筆者經驗而談：1×104m3挖填量以內，控制在5%以內，1×104m3～10×104m3控制在3%范圍內，10×104m3以上控制在1%～2%的范圍內是較為合理的誤差范圍。

4.總論

綜上所述，在我們的實際工作中，若較為準確計算出土（石）方挖填客觀實際計算量，必須經過以下過程：

（1）客觀準確地加密地形點，尤其是陡坎、坡面等。這往往是地形點較為缺失的地方，也是土（石）方計算的決定性特征。

（2）建立DTM數據模型。根據所反應的特征與實地對照，反復增加地形點，直到模型與實地一致。

（3）選擇多種土（石）方計算方法，擇其優者，得出結論。

（4）土（石）方計算的誤差率，應該隨著土（石）方計算量的增大而減小。

參考文獻：

[1]《Cass91 For Aotocad 2008》廣州南方數碼科技有限公司編著，2012版.

[2]《工程測量規范》GB50026-2007，國家技術監督局和中華人民共和國建設部聯合頒布.

[3]《1∶500_1∶1000_1∶2000外業數字測圖技術規程》GB14912-2005中華人民共和國國家質量監督檢驗檢疫總局、中國國家標準化管理委員會發布.

[4]萬義有，李勇華，王小衛.土方量計算中的方格網法邊長最優選擇分析[J].科技資訊，2018（19）：65-68.

[5]田旦，成國輝，徐景，熊仕穩.方格網法土方計算精度提高的改進方法[J].城市勘測，2017（03）：148-150+170.

[6]邱文雙.方格網法在復墾工程土方量計算中的應用[J].礦山測量，2017，45（03）：114-116.

[7]楊永平，陳占，張曉倫.關于方格網法計算土方公式的探討[J].昆明冶金高等專科學校學報，2016，32（05）：57-61.

[8]曾懷恩，葛奎.利用方格網法計算復雜地形開挖土方量[J].地理空間信息，2016，14（09）：82-84+8.

[9]張衡，李通，肖鵬，吳學超，徐花芝.利用方格網法計算土石方量的探討[J].山西建筑，2016，42（04）：217-218.

[10]劉宏宏.方格網法土石方計算與高程中誤差關系的探討[J].江西測繪，2016（01）：57-58.

[11]廖小延，熊俊杰.方格網法計算土方量的應用分析[J].城市勘測，2015（01）：155-158.

[12]粟晟，歐陸.南方CASS計算兩期間土方與方格網法土方計算相結合準確計算土方量[J].中國井礦鹽，2013，44（05）：32-34+37.

[13]曹祥寅，趙崇陽.淺談方格網法土石方算法在土石方工程中的應用[J].廣東科技，2013，22（02）：86-87.

[14]黃紅鎮.土方工程計算若干問題的思考——以FastTFT方格網法為例[J].中外企業家，2018（23）：113.

[15]徐劍，王振.方格網法土方計算在公路服務區場地計算中的應用[J].工程與建設，2018，32（01）：33-36.

[16]劉士霞.基于CASS方格網法土方量計算應用[J].水土保持應用技術，2018（01）：34-35.