數據缺失環境下基于DCTPLS-PCA的路網速度預測研究

姚加林，朱闖

數據缺失環境下基于DCTPLS-PCA的路網速度預測研究

姚加林，朱闖

(中南大學 交通運輸工程學院，湖南 長沙 410075)

準確可靠的短時交通流預測是實現良好交通控制與誘導的基礎，由于設備故障和通信干擾等原因，交通數據經常存在缺失現象，給交通流預測造成了很大困難。在數據缺失環境下，通過基于三維離散余弦變換的補償最小二乘回歸(DCT-PLS)算法對缺失數據進行修復，利用主成分分析(PCA)對修復后的數據降維，用K近鄰(KNN)算法預測路網中各路段速度，并計算預測誤差。以長沙市某路網為例，在數據完整和數據缺失2種情況下進行數值實驗。研究結果表明：DCT-PLS算法修復精度高于概率主成分分析(PPCA)和貝葉斯主成分分析(BPCA)；PCA降維能夠大幅減少預測時的計算成本；在數據缺失環境下，基于DCTPLS-PCA的方法在大幅降低計算成本的同時，能夠保證很好的預測精度。

數據缺失；DCT-PLS；PCA；路網；速度預測

隨著經濟社會的快速發展，小汽車保有量急劇增加，由此導致了日益嚴重的城市交通擁堵問題。智能交通系統被認為是緩解城市交通擁堵的重要方案之一，交通控制與誘導是城市交通管理中的重要組成部分，在智能交通系統中發揮著舉足輕重的作用。而準確可靠的短時交通流預測是實現良好交通控制與誘導的基礎，因此研究短時交通流預測對于緩解城市擁堵具有重要意義。數據采集是實現交通流預測的第一步，然而在交通數據采集過程中，由于設備故障、通信干擾等原因，經常存在數據缺失現象，這給準確的交通流預測造成巨大困難。在加拿大亞伯達7 a的交通數據中有近50%的數據存在缺失，某些時段缺失比例更是高達90%[1]。數據修復是處理缺失數據的常用方法，數據修復算法可分為3類，第1類為基于向量的修復方法，包括近鄰方法[2]，回歸補值方法[3?4]等。第2類為基于矩陣的修復方法，包括概率主成分分析(PPCA)和貝葉斯主成分分析(BPCA)[5?6]等。第3類為基于張量的修復方法，包括CP分解方法和Tucker分解方法[7]等。基于矩陣的修復方法具有修復精度高、速度快的優點，在交通數據修復領域應用廣泛，PPCA和BPCA是其中常用的2種算法。但是當缺失率高時，上述2種算法的修復結果不盡如人意。基于三維離散余弦變換的補償最小二乘回歸(penalized least square regression based on three-dimensional discrete cosine transform，DCT-PLS)算法在高缺失率時仍能保證很高的修復精度[8?9]，本文首次將該算法引入交通數據修復領域。以往的研究[10?12]多是預測單個路段上車輛的速度，但是單個路段的交通信息對于交通管理與控制的指導作用有限，因此，本文以路網為研究對象，預測路網內各路段的速度，為交通管控提供更全面的信息。當研究對象由路段擴展為路網，帶來了數據量激增的問題，特別是對于數據驅動的預測方法而言，數據量的激增會導致難以承受的計算成本。為解決該問題，引入數據降維技術以降低計算成本。主成分分析(Principal Component Analysis，PCA)計算簡單，易于實現，是常用的降維方法，本文采用該方法對修復后的數據降維。綜上，在數據缺失環境下，本文首先采用DCT-PLS算法對缺失數據進行修復，然后應用PCA算法對修復后的數據降維，最后以該數據作為實驗數據，用K近鄰(K nearest neighbors，KNN)算法預測路網內各路段速度。

1 研究方法

1.1 DCT-PLS算法

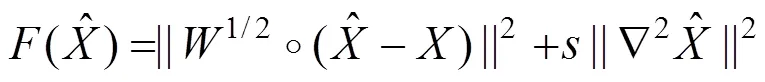
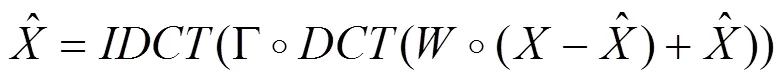
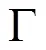
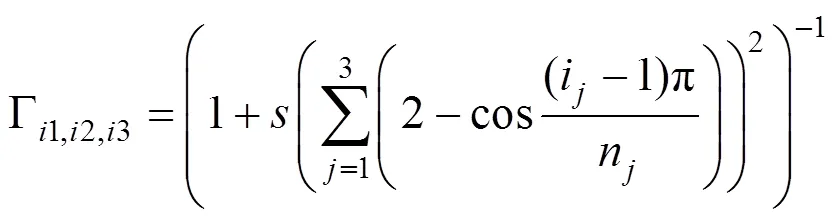
其中：i表示第維的第個元素，n表示的第維的大小。

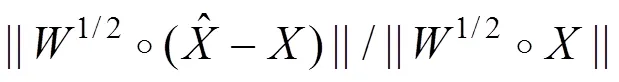
根據歸一化誤差，即可由DCT-PLS預測缺 失值。

1.2 PCA算法

PCA是一種統計方法。通過正交變換將一組可能存在相關性的變量轉換為一組線性不相關的變量，轉換后的這組變量叫主成分。其步驟為：

1) 數據標準化：設有個向量，個樣本點的矩陣，將矩陣標準化，得到矩陣矩陣的相關系數矩陣設為。

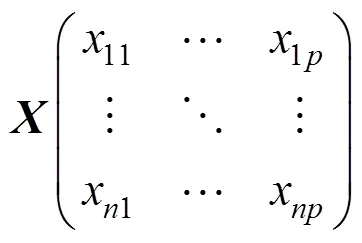
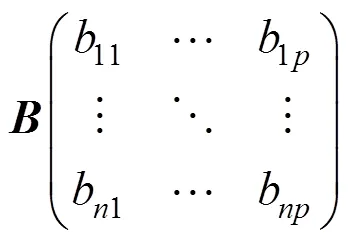
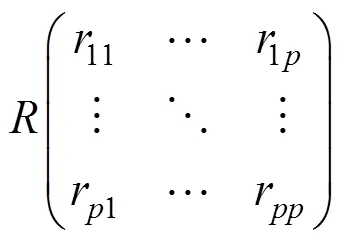
其中：

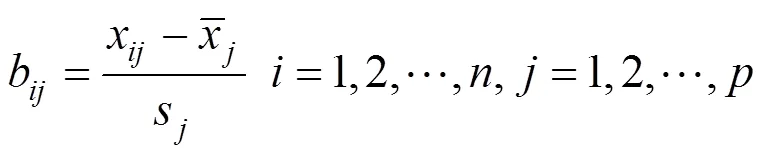
2) 計算矩陣的特征值與特征向量：解特征方程求得特征值λ(=1, 2, …,)然后求出特征值對應的正交化單位特征向量e(=1, 2, …,)

3) 計算主成分貢獻率及累計貢獻率

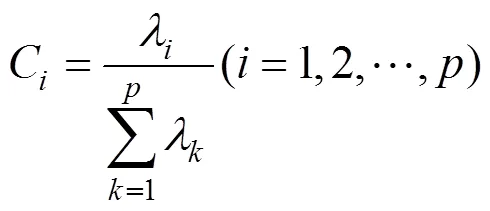
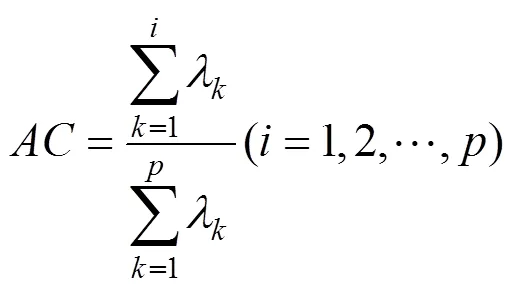
4) 計算主成分載荷

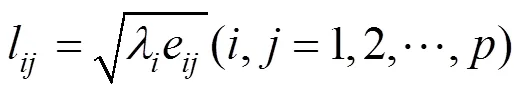
5) 計算各主成分得分

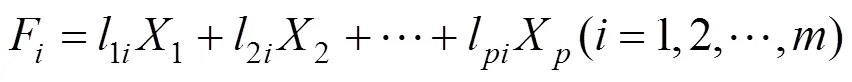
其中：為選取的主成分個數，其值取決于使用者選定的累計貢獻率閾值。

1.3 KNN算法

K近鄰(KNN)算法是一種典型基于數據驅動的算法，具有參數少，易于拓展的優點。其算法步驟如下：

1) 將數據分成2部分，一部分作為訓練數據，另一部分作為測試數據。

2) 選定參數

3)維護一個大小為，按距離由小到大排列的最近鄰數組；維護一個大小為K的優先級隊列。

4) 遍歷訓練數據，計算當前訓練數組與測試數組的距離，將該距離與最近鄰數組中最大距離max比較。

5) 若>=max，則舍棄該數組，遍歷下一個數組。若＜max，刪除優先級隊列中最大距離的數組，將當前訓練數組存入優先級隊列。

6) 遍歷完畢，計算優先級隊列中個數組的多數類，并將其作為測試數組的類別。

2 實驗場景與數據處理

2.1 實驗場景

選取長沙市中心城區某一路網為研究對象，該路網內包含4個信控交叉口和26個路段。路段上的出租車GPS數據被用來估算該路段上車輛的平均速度。GPS數據包含以下信息：路段編號、每個路段上出租車數量、出租車運行速度、時間戳等。該數據的采樣間隔為2 min，因此每天采集720個數據。本文使用16 d共11 520個數據作為實驗 數據。

實驗路網圖如圖1所示，其中圖1(a)為衛星圖；圖1(b)為路網拓撲結構圖，為方便表示和閱讀，將路段重新進行了編號。

圖1(a)中未被編號的建湘路將蔡鍔路和芙蓉路之間的人民路分為2個路段(即路段1070201/ 1070301，相反方向為1070303/1020703)，在此情況下，本文將同方向2個路段視為一個路段(路段11，相反方向編號12)，其速度值取2個路段上車輛速度的平均值。因此，實驗路網中總包含24個路段。

2.2 數據缺失形式

在數據采集過程中，由于設備故障、通信干擾等原因，采集到的數據經常存在缺失的情況。根據缺失的形式不同，可以分為3種形式即隨機缺失、模塊缺失和混合缺失。本文中，在隨機缺失情況下，產生一系列隨機位置，該位置的數據缺失，用NaN代替。在模塊缺失情況下，產生一系列隨機位置，該位置及之后的個數據連續缺失(本文取10)，用NaN代替。值得注意的是，該隨機數序列中，各隨機數之間的差值不得小于-1。當數據混合缺失時，首先將數據平均分為2部分，一部分數據采用隨機缺失的方法處理，另一部分采用模塊缺失的方法處理。將數據分組可以避免出現同一個數據多次缺失的情況。

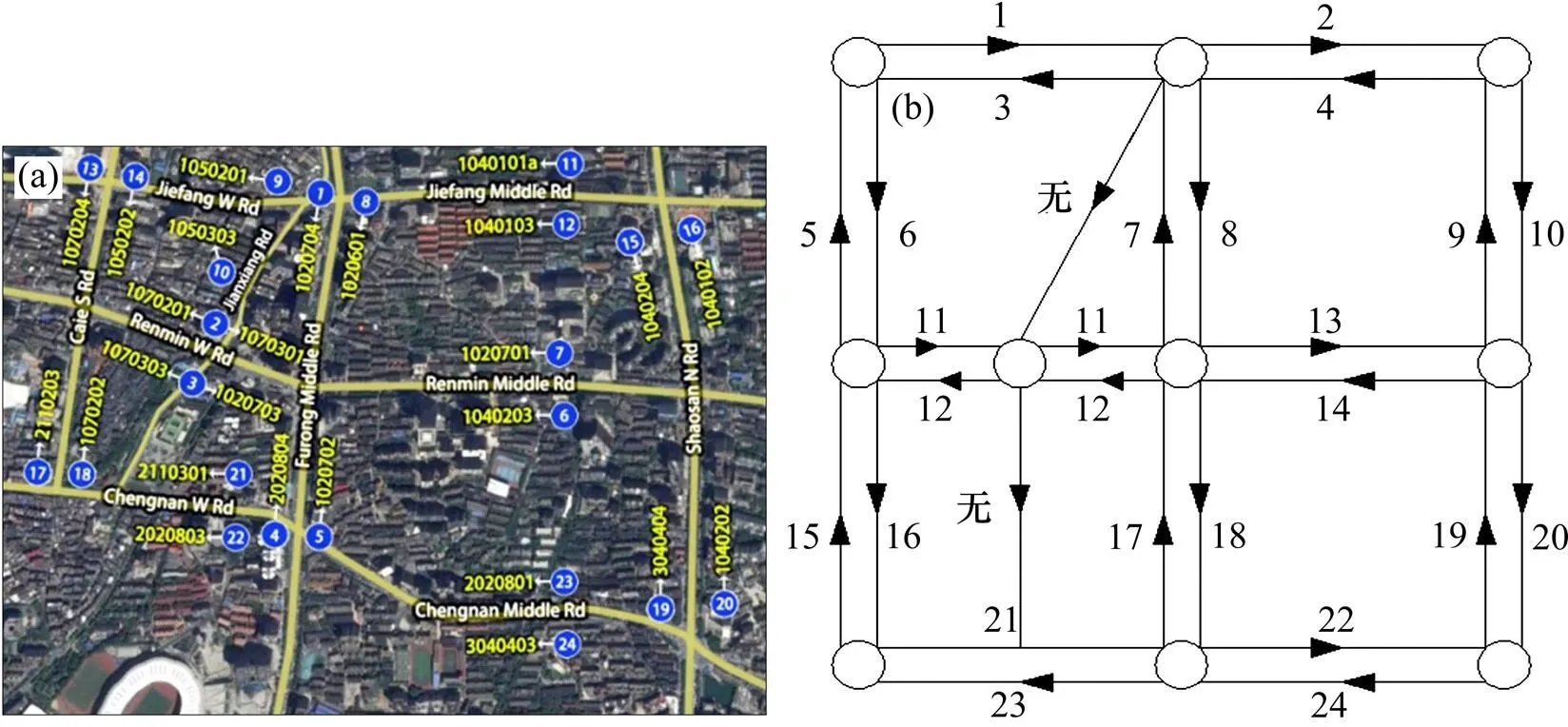
(a) 衛星圖；(b) 拓撲結構圖

另外，為了衡量修復誤差及預測誤差，采用3個常用指標，即平均絕對誤差(Mean Absolute Error，MAE)、平均絕對百分比誤差(Mean Absolute Percent Error，MAPE)、均方根誤差(Root Mean Square Error，RMSE)。

3 數值實驗

3.1 修復算法比較

PPCA和BPCA是修復交通數據常用的算法，本文從修復精度和計算時間2個維度比較PPCA、BPCA與DCT-PLS。

實驗數據缺失率從10%開始，以10%的步長遞增至90%。因為數據缺失位置(或缺失起始位置)是隨機產生的，為了降低隨機因素對實驗結果的影響，每種缺失率下均進行10次重復實驗。

表1~3列出了10次實驗的平均MAPE(10次實驗結果方差很小，這里沒有列出)。值得注意的是，表中列出的時間為90次實驗的總時間。另外，在缺失率較高時，BPCA算法在短時間內(10 min)無法完成修復工作，因此，表中沒有列出其相應的修復誤差及總計算時間。

從表1可知，隨機缺失時，在各缺失率下，DCT-PLS的修復精度均最高。當缺失率超過70%時，DCT-PLS的修復精度比PPCA高出10%。PPCA的修復精度較DCT-PLS略低，但是其運行速度更快。BPCA在缺失率不超過50%時，修復精度與PPCA及DCT-PLS相當，但是隨著缺失率進一步增加，該算法難以在短時間內完成修復工作。

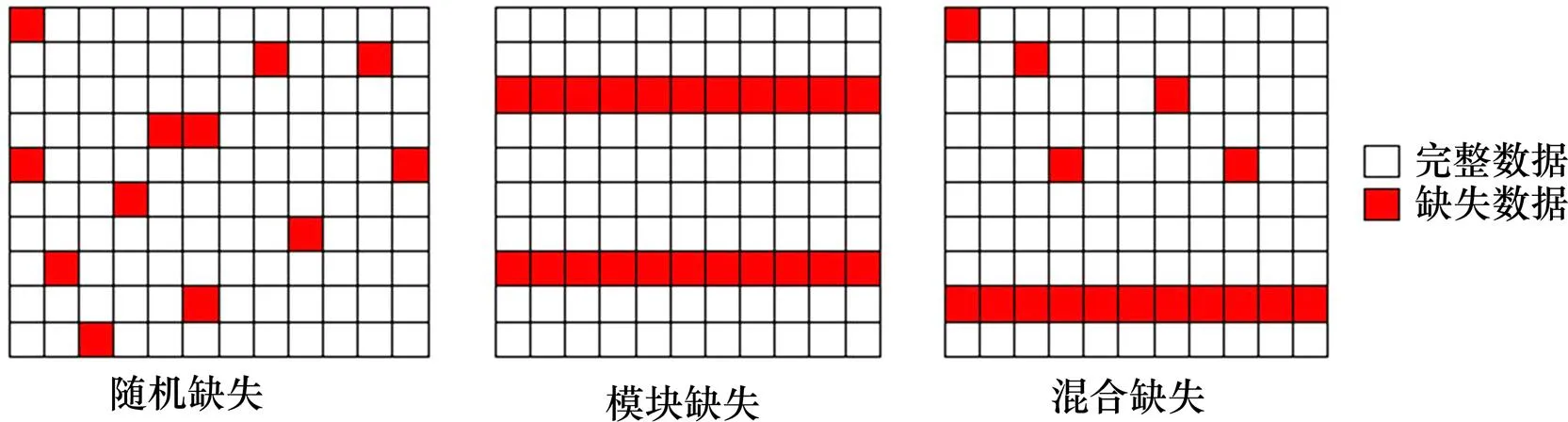
圖2 3種缺失形式示意圖

表1 隨機缺失下不同算法修復誤差

表2 模塊缺失下不同算法修復誤差

表3 混合缺失下不同算法修復誤差

模塊缺失時，由表2可知，當缺失率不超過50%時，PPCA修復精度最高，隨著缺失率繼續增加，PPCA的修復誤差增長較快。

DCT-PLS在高缺失率時優勢明顯，當缺失率達到80%時，其誤差低于20%，且較PPCA低10%左右。BPCA在低缺失率時修復精度與PPCA及DCT- PLS相近，但是當缺失率較高時，該算法的計算成本迅速增加。

與模塊缺失類似，混合缺失時，由表3可得，缺失率較低時，PPCA修復較高，隨著缺失率增加，其修復誤差快速增加。隨著缺失率增加，DCT-PLS的修復誤差也逐漸增加，但是其誤差增長幅度小于PPCA,特別是缺失率高于60%后，其誤差增長明顯低于PPCA。BPCA同樣在低缺失率時修復精度較好，但是無法在短時間內完成高缺失率數據的 修復。

綜上所述，相較于PPCA、DCT-PLS，BPCA算法在修復精度和運算時間上均沒有優勢。PPCA算法計算速度快，在低缺失率時，修復精度高，當缺失率不超過50%時，建議采用PPCA算法進行數據修復。DCT-PLS算法計算速度較PPCA略慢，但是在各種缺失率下，其修復精度均較高，特別是高缺失率時(缺失率>60%)，其修復精度明顯高于另外2種算法，因此在高缺失率時，建議采用DCT-PLS算法。后續的預測實驗中數據缺失率很高，因此采用DCT-PLS作為本文的修復算法。

3.2 預測實驗

3.2.1 實驗參數設定

本文將前15 d的數據作為KNN算法的訓練數據，第16 d數據作為測試數據，同時，根據經驗將K近鄰算法中K值設為5。因為GPS數據周期為2 min，因此本文的預測周期設為2 min。另外，模塊缺失中參數設為10，主成分分析中累計概率閾值取值設為90%。

3.2.2 數據完整情況

在數據完整情況下，不需要使用DCT-PLS修復數據，直接用PCA算法對數據降維。數據降維后，使用KNN算法預測。

一次預測能夠輸出全部24個路段的預測值及相應誤差，但是由于版面限制，無法對各個路段進行單獨分析，因此取24個路段的平均誤差作為路網的預測誤差，結果見表4。

由表4可知，在數據完整情況下，KNN能較好的預測路網上各路段的速度值。

表4 數據完整情況下路網預測誤差

3.2.3 數據缺失情況

在數據缺失情況下，首先使用DCT-PLS算法對缺失數據進行修復，之后用PCA方法降維，最后使用KNN算法預測。同樣的，為了避免隨機因素對結果的影響，每組實驗重復10次。

表5列出來了數據降維的結果(10次實驗平均值)。同樣的，由于版面限制，無法對路網內各路段的預測結果進行單獨分析，只列出路網內所有路段的平均預測誤差。表6~8中列出了10次實驗的平均誤差，圖3以盒圖的形式展示了10次實驗的 結果。

另外，城市交通網絡具有很強的時效性，為了驗證本文提出的方法的廣泛適用性，在3種缺失形式下，分別計算了全天平均預測誤差(即表6)，8:00~9:00時段的誤差(表9)及20:00~21:00時段的預測誤差(表10)。

表5 PCA降維后列向量個數

表6 隨機缺失下路網平均誤差

表7 模塊缺失下路網平均誤差

表8 混合缺失下路網平均誤差

表9 隨機缺失下路網平均誤差(8:00~9:00)

表10 隨機缺失下路網平均誤差(20:00~21:00)

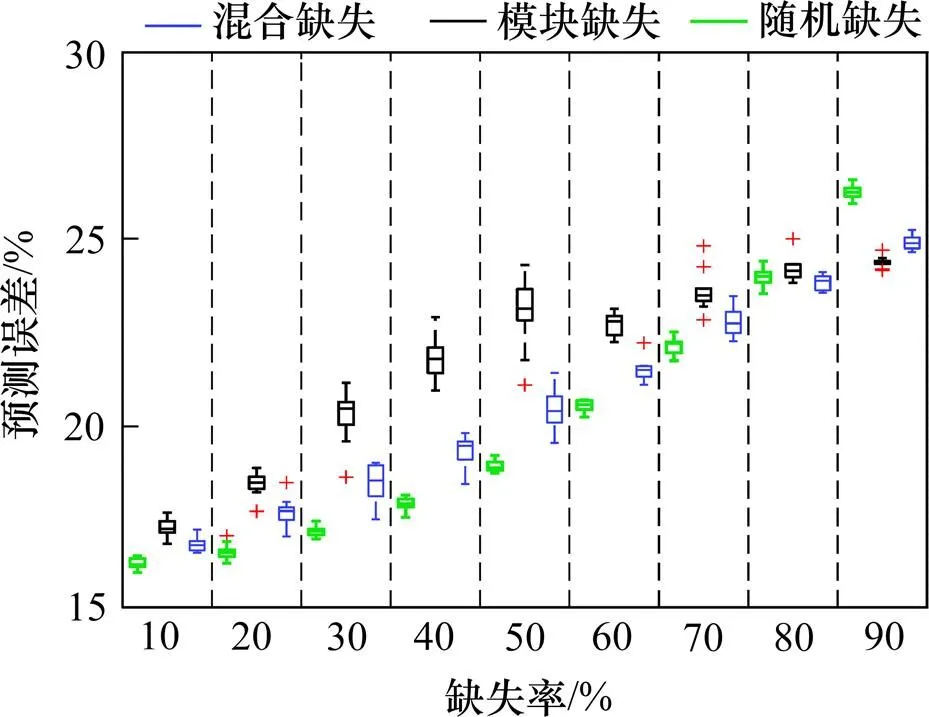
圖3 10次實驗預測誤差(MAPE)

由表5可知，應用PCA之后數據變為2-12列，降維之后的數據量約為原始數據的1/12-1/2(降維之前數據由24個列向量組成(24個路段))。比較不同缺失率的降維效果可知，缺失率越高降維后剩余的數據量越少。當缺失率為90%時，降維后的數據量僅為原始數據的1/12，與原始數據中不缺失數據量(10%)相當。另外，本文中應用PCA完成一次降維所需時間約為0.5 s，相對于預測時間可以忽略不計，因此使用數據降維技術可以大幅降低基于數據驅動的預測方法的計算成本。

從表6可知，隨著數據缺失率的增加，平均誤差也相應增加。當缺失率為10%時，預測誤差為16.18%，與不缺失時的誤差相近；當缺失率為50%時，預測誤差為18.82，比不缺失時增加2.80%；當缺失率達到90%時，MAPE也僅為26.53%，較數據完整時增加了10%，MAE為4.6511，較不缺失時增加約0.8。

在模塊缺失時，由表7可得，預測誤差同樣隨著缺失率增加而逐漸增加。缺失率為10%時，誤差為17.15%，較數據完整時增加1.13%；缺失率達到90%時，MAPE為24.33%，較不缺失時僅增加8%，而MAE為4.508 0，比不缺失時增加約0.7。

由表8可知，混合缺失時，當缺失率在50%以下時，預測誤差均小于20%，較不缺失情況僅僅增加4%。當缺失率繼續增加時，預測誤差隨之增加，但是增加幅度較小。缺失率為90%時，誤差也僅為24.87%，較不缺失時僅僅增加了8%，MAE為4.529 0，比不缺失時增加約0.7。

在隨機缺失環境下，由表6、表9可知，8:00~ 9:00時段的預測誤差低于全天平均誤差。對比表6和表10可知，20:00~21:00時段的MAE及RMSE值低于全天的對應值，但是其MAPE值比全天平均MAPE值高。全天平均、8:00~9:00時段及20:00~ 21:00時段的預測誤差存在差異但預測精度均較好。在模塊缺失及混合缺失環境下可得出與隨機缺失環境下相同的結論。

從圖3中可以看出,隨著缺失率增加，MAPE值隨之增加(對MAE、RMSE有相同結論)。比較不同缺失形式可知，隨機缺失時預測效果最好，混合缺失次之，模塊缺失最差。另外，從盒圖可以看出不同缺失率下，隨機缺失時10次實驗結果的方差最小，模塊缺失與混合缺失方差相近。

4 結論

1) PPCA算法效率最高，DCT-PLS算法效率略低，BPCA算法的效率明顯低于上述2種算法。在低缺失率時，3種算法的修復精度相近；在高缺失率時，DCT-PLS算法優勢明顯，其修復精度比PPCA高10%左右。

2) 使用PCA算法降維后數據量變為原來的1/2-1/12，說明使用降維技術可以大幅減少數據量，從而降低預測時的計算成本。

3) 3種缺失形式下，當缺失率為10%時，預測誤差較數據完整時僅增加1%左右，當缺失率達到90%時，預測誤差也僅增加10%左右，證明在數據缺失環境下，基于DCTPLS-PCA的方法在大幅降低計算成本的同時，能夠保證很好的預測精度。

[1] 徐健銳, 李星毅, 施化吉. 處理缺失數據的短時交通流預測模型[J]. 計算機應用, 2010, 30(4): 1117?1120. XU Jianrui, LI Xingyi, SHI Huaji. Short-term traffic flow prediction model for processing missing data[J]. Computer Applications, 2010, 30(4): 1117?1120.

[2] Smith B, Scherer W, Conklin J. Exploring imputation techniques for missing data in transportation management systems[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003(1836): 132? 142.

[3] CHEN C, Kwon J, Rice J, et al. Detecting errors and imputing missing data for single-loop surveillance systems[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003 (1855): 160? 167.

[4] ZHONG M, Lingras P, Sharma S. Estimation of missing traffic counts using factor, genetic, neural, and regression techniques[J]. Transportation Research Part C: Emerging Technologies, 2004, 12(2): 139?166.

[5] QU L, LI L, ZHANG Y, et al. PPCA-based missing data imputation for traffic flow volume: A systematical approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(3): 512?522.

[6] LI L, LI Y, LI Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence[J]. Transportation Research Part C: Emerging Technologies, 2013(34): 108?120.

[7] Kolda T G, Bader B W. Tensor decompositions and applications[J]. SIAM Review, 2009, 51(3): 455?500.

[8] Garcia D. Robust smoothing of gridded data in one and higher dimensions with missing values[J]. Computational Statistics & Data Analysis, 2010, 54(4): 1167?1178.

[9] WANG G, Garcia D, LIU Y, et al. A three-dimensional gap filling method for large geophysical datasets: Application to global satellite soil moisture observations [J]. Environmental Modelling & Software, 2012(30): 139?142.

[10] ZHENG L, ZHU C, ZHU N, et al. Feature selection- based approach for urban short-term travel speed prediction[J]. IET Intelligent Transport Systems, 2018, 12(6): 474?484.

[11] TANG J, LIU F, ZOU Y, et al. An improved fuzzy neural network for traffic speed prediction considering periodic characteristic[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(9): 2340?2350.

[12] MA X, DAI Z, HE Z, et al. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction[J]. Sensors, 2017, 17(4): 818.

Research on road network speed prediction based on DCTPLS-PCA under data missing

YAO Jialin, ZHU Chuang

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Accurate and reliable short-term traffic flow prediction is the basis of traffic control and guidance. However, traffic data missing that result from communication interference and other reasons, makes traffic flow prediction difficult. In this paper, the compensated least square regression algorithm (DCT-PLS) based on 3D discrete cosine transform was used to repair the missing data, and then the dimension of the repaired data was reduced by principal component analysis (PCA). Finally, the K-nearest neighbor (KNN) algorithm was used to predict the speed of each link of the road network, and the prediction error is calculated. The numerical experiments were conducted with and without the data missing based on a real network information in Changsha. The results show that the accuracy of repairing data of DCT-PLS algorithm is higher than that of probabilistic principal component analysis (PPCA) and Bayesian principal component analysis (BPCA); PCA can greatly reduce the computational cost of prediction. Under data missing, the method based on DCTPLS-PCA can greatly reduce the computational cost and ensure good prediction accuracy.

data missing; DCT-PLS; PCA; road network; speed prediction

U491

A

1672 ? 7029(2019)10? 2612 ? 08

10.19713/j.cnki.43?1423/u.2019.10.030

2019?01?01

姚加林(1961?)，男，湖南婁底人，副教授，從事交通運輸規劃與管理研究；E?mail：yaojialn@csu.edu.cn

(編輯 蔣學東)