數學課堂中幾個常見“遺憾”的剖析和反思

浙江省寧波市第七中學 姚力嬌

動態生成的課堂是真實的，體現的是新課程的理念，但隨之出現的是教師無法預料的情況，難免會帶著或多或少的遺憾.不過，作為新課改背景下的教師，我們無需苛求完美無缺的課堂，但需學會關注、捕捉和反思每一節課中的遺憾，并努力找尋方法彌補和改進，讓數學課堂更靈動、更優化.那么，我們如何不斷反思和改進教學中的缺失現象呢？本文中，筆者選取具有典型意義和探究價值的教學片段或一些實施環節進行案例分析，反思課堂中常見的教學遺憾.

一、教師過度讓位的“遺憾”

新課改風向標下，師生的角色也發生了重大改革，學生的主體地位越發凸顯，“以生為本”已成為教學的一種習慣.這樣一來，不少教師便會片面地認為，無論是什么教學內容，不管是什么教學目標，放權給學生，讓學生親歷知識的形成便是對學生主體地位的一種肯定.學生的主體地位放大化，教師轉變成教學過程中的一個旁觀者，這種過度讓位的現象實際上是對學生主體的一種放任自流，教學效果也是可想而知的.

案例1：以“直線和圓的位置關系”（第2課時）的教學片段為例.

首先，教師以“任務串”的形式快速導入課堂：翻開教材并仔細閱讀第38至39頁除練習以外的內容，并獨立完成活動單，然后小組合作交流，最后分組展示，比一比哪個小組的學習更有效.學生快速投入到自主學習中，仔細研讀教材，不少學生能準確圈出概念中的關鍵字詞；一個個都能認真思考活動單上的問題并一一解決，最終一個解決問題讓大部分學生“卡殼”了.

例題：如圖1所示，OM為∠AOB的角平分線，點P是OM上一點，現以點P為圓心作⊙P，⊙P和OA相切，且切點為D.求證：⊙P與OB也相切.

事實上，教師很快便發現了學生的“卡殼”現象，但他并沒有施以援手或引導學生小組合作討論，大概是不想過早介入，不想給予學生過多的牽制.

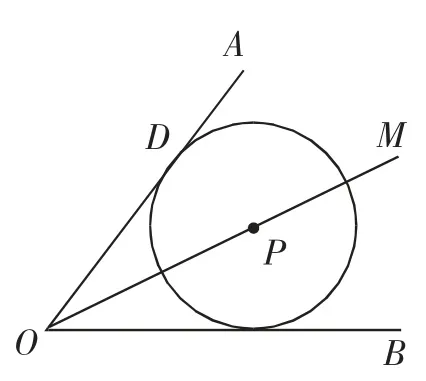
圖1

隨著時間的流逝，學生再也按捺不住，展開了一番討論……教師僅僅是這組聽聽，那組看看，整個過程保持沉默，似乎僅僅是實施課堂教學的“監控”.展示環節有條不紊地開始了，終于輪到了這道讓大多數學生困惑不已的題了.此時距離下課僅剩6分鐘.

生1：我認為點P作為∠AOB的角平分線上一點，可以過點P作OA和OB的垂線……

生2：你這樣是錯的，應該連接點P和點D，不然的話過點P作OA的垂線不和點D重合嗎？

師：還有其他不同意見嗎？

此時，教師顯然有些著急了.他這里想呈現的結論是：若題設中呈現了直線與圓的公共點，則“連接半徑，證明垂直”即可；若題設中未呈現直線與圓的公共點，那么就需“作垂直，并證半徑”.

不過，此刻學生面面相覷、滿臉疑惑，無法作答.

反思：此案例中學生自主學習、合作交流的過程一覽無遺，充分體現了學生的主體地位.但是，學生對于切線三種判定方法掌握了幾分？會添加輔助線嗎？此處的數學本質僅憑學生閱讀教材是無法領悟的，這些必須由教師以“問題鏈”進行引導，由學生展開辯論方可實現.

可以在原有教學過程的基礎上改一改，牢牢把握學生“迫切生成”的時機，由以下一系列“問題鏈”為指引，引導學生在分析和辯論中突破教材中的難點，并落實重點：

（1）如圖2所示，直線l是否為⊙O的切線？

讓學生清楚不能依靠直觀判斷，判定方法之一是定義法，需明示直線與圓有唯一的公共點.

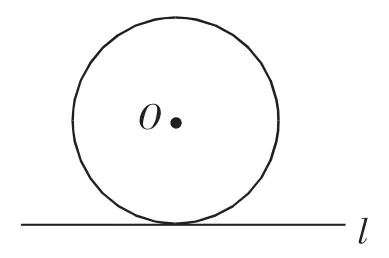
圖2

（2）若⊙O的直徑是10cm，點O到直線l的距離是5cm，那么直線l是否為⊙O的切線？

讓學生清楚判定方法之二“d=r法”，可以通過計算來判定.

（3）如圖3所示，已知⊙O上有一點A，過點A的直線l和半徑OA在滿足什么條件時，可證明直線l為⊙O的切線？這種判定法與“d=r法”有何區別？

對判定法進一步鞏固，讓學生清楚這里所用的定理就是從推理角度判定的“d=r法”.

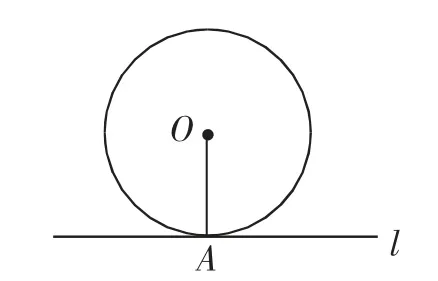
圖3

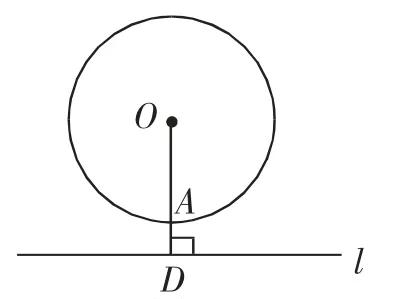
圖4

（4）如圖4所示，過圓心的直線OD與⊙O相交于點A，且直線OD垂直于直線l，現將直線l向上平移，當平移到哪個位置時，直線OD和⊙O第一次相切？

讓學生清楚此題的本質也是判定法“d=r法”.

（5）分析用切線判定定理證明某直線為圓的切線存在幾種情況，并思考與之對應的證明策略是什么.

總結歸納出案例中教師嘗試呈現的結論.

教材是引領學生認知發展和建構知識的“中介”，也就是說，教材是實施教學的范例，是師生之間交往互動的平臺.這就要求教師主動設計和開發教材，從“教”教材轉變為“用”教材，將教材中的知識本質提煉出來，生成自身的數學思考，促進學生的發展.同時，在教學過程中，教師應當智慧地開展教學，關注學情，以學定教，及時給予學生點撥和誘導，創造性地開展教學，讓課堂成為自主學習的課堂，而非放任自流的課堂.

二、淺顯數學理解的“遺憾”

專家與一線教師一致認為，新課程改革的三大基石為理解數學、理解學生、理解教學.然而現實教學中，相當一部分教師在第一基石方面存在著一定的遺憾，自身對數學理解淺顯，導致教學淺顯，教學效果自然是低效的.

案例2：以“待定系數法求一次函數解析式”的教學片段為例.

教師用“直入式”揭題后引導學生閱讀教材，并回到以下問題：

（1）什么是待定系數法？

（2）運用待定系數法求一次函數的解析式有哪些步驟？

（3）分析例題，嘗試解決以下問題.

（4）在問題解決的過程中，需注意哪些問題？

本章節的知識與方法都呈現單一化的特點，再加以例題的輔助，更適宜通過學生自學來完成教學過程，并可以較為高效地完成教學任務.

反思：思考并反思教學過程，在案例的教學過程中，似乎存在著一些遺憾.比如，觀察表1并寫出y與x之間的函數關系式：

表1

學生可以正確填寫這個表格嗎？答案是不確定.此案例中，學生的學習過程僅僅是學習的第一階段“模仿”，對“用待定系數法求一次函數解析式”的認識不夠深刻.筆者認為，需從以下三個方面進行滲透：

第一，需讓學生明確函數的類別.教師需將例題中出示的“一次”略去，采用引導學生合作討論的方式，使學生對這里的函數解析式有一個清楚的認識.

第二，需讓學生明確函數的一般表達式.即使前一個課時中已然借助生活實例充分概括，但此課中仍需進行不斷強化和鞏固.

第三，需讓學生明白待定系數的個數與序數對的個數應當一致.筆者認為，本課的教學重點之一為“變式中活用待定系數法求一次函數解析式”.我們可以借助文字型、圖像型、表格型的題目，去設置開放題，讓學生在富有“數學味”的課堂中厘清重、難點，充分開發學生的潛能，創設高效數學課堂.

總之，在教學中，伴隨著教學的深入，學生會生成各種想法和質疑.教師則需依據學生的具體情況厘清思想脈絡，觀察學生的思維走向，并隨時隨地地調整教學策略，讓學生成為課堂的主人.教師還需充分理解數學，引導學生去實踐、思考、探究、交流等，獲得數學的基礎知識、基本技能、基本思想、基本活動經驗，促進學生積極主動、富有個性地學習.當然，帶有遺憾的課堂才是真正靈動的課堂，但我們需厘清遺憾所在，并不斷找尋策略調整和彌補，讓遺憾不斷成熟我們的課堂，讓師生共同在遺憾中成長.