培養高中學生數學運算能力的案例與思考
☉江蘇省通州高級中學 姚振飛
集算理、算法、計算、推理、轉化等多種數學思想方法于一體的運算能力對于數學學習及相關學科的學習來說都是極為關鍵的,但很多高中生對運算能力的忽視導致其運算能力低下并最終影響到數學學習的整體效果.教師應該能夠注意到運算能力對于數學學習的重要影響,并在實際教學中關注學生運算能力的訓練.
一、運算能力的涵義和層次
運算能力這一綜合性能力是不可能獨立于其他能力而獨立存在與發展的,和記憶能力、理解能力、表達能力、邏輯推理能力、解題能力相互滲透與支持的運算能力在發展上應與其他能力同步進行,教師應充分關注到這一點,并在教學中恰當滲透培養學生運算能力的教學以促進學生的數學學習進步.
運算能力其實包含著很多方面的內容,學生對算理、公式、法則的記憶、理解和正確運用是運算能力的最基本的內容,對數、式、方程、映射、向量等進行運算與變形屬于更高層次的運算,除此以外,尋求并設計合理而簡捷的運算途徑、估算或近似計算及數據處理、思維能力與思想方法在運算中的滲透、運算品質與心理素質、運算速度等都是包含在運算能力范疇內的內容.
運算能力具有一定的層次性,理解、記憶及運用算理、公式和法則是屬于最低層次;掌握數、式、方程、映射、向量的運算、變形的基本技能屬于運算能力三個層次中的第二層次;計算中發揮思維作用并尋求、設計合理而簡捷的運算途徑,具備較高的運算速度、準確率及穩定的心理素質則屬于最高層次.
由此可見,運算能力是從低層次向高層次發展的,教師在學生的運算能力訓練中應著眼于基礎,縱觀全局并結合知識水平與其他能力的發展進行有針對性的訓練,使學生能夠在循序漸進的反復訓練中獲得各層次的運算能力的發展.
二、培養途徑
對運算能力的發展過程進行分析可以發現,培養學生運算能力的途徑主要有以下三個方面:
1.在算理、公式、法則的理解、記憶和運用上進行針對性的教學和訓練
充分認識、理解算理和法則是提升學生運算能力中最基本的一個步驟,因此,教師在培養學生的運算能力上首先應關注到以下兩點:
第一,提出公式、例示運用的教學模式在算理、公式、法則的理解與記憶教學中并不具備特別的價值,重視算理、公式、法則的形成過程并引導學生深刻認識其本質能使學生在理解的基礎上產生牢固的記憶.
例1試求(1-2x+3x2)6展開式中x5項的系數.
分析:如果運用二項式定理和通項公式對此題進行直接求解將會產生相當煩瑣的運算過程,但如果能夠領會并運用組合原理來求解x5項的系數則會簡捷許多.
解:展開式中含x5的項有(-2x)5,(-2x)3·(3x2),(-2x)·(3x2)2這三種類型.根據組合原理,展開式中含x5的項為因此(1-2x+3x2)6展開式中x5項的系數為-2712.
第二,引導學生在靈活運用算理、公式、法則中加深理解與記憶.比如:
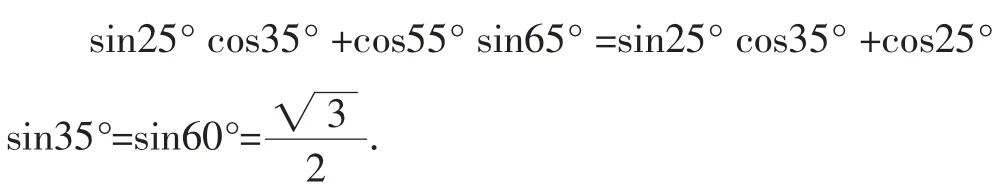
教師在實際教學中重視此類運算的訓練才能令學生對兩角和與差的公式產生更好的理解與記憶.
2.關注數學思想方法的應用
運算能力發展成為運算基本方法與技能意味著運算能力已經發展到了中級水平,這一過程隱含著數學思想方法所起到的積極意義與作用,等價轉化與數形結合就是這一過程中經常用到的數學思想方法.
教師應該能夠關注到轉化思想在運算中的具體體現形式并幫助學生獲得切實的掌握,一般來講,其中重要的技能有下述幾種.
(1)配湊(配方)變形.
例2求tan20°+tan40°+tan20°tan40°的值.
解析:將原式變形為:
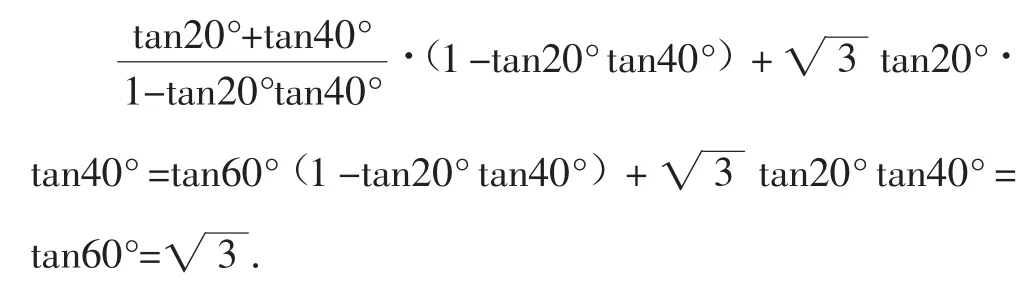
從此題的求解過程可以看出,配湊(配方)變形在解題中起到了特別重要的作用.
(2)適當換元.
例3求函數的值域.
解析:令,則x-1=t2(t≥0),故y=t2-2t+4=(t-1)2+3,因此函數的值域為[3,+∞).
(3)整體代換.
例4已知等比數列{an},若公比q≠±1,S10=8.試求的值.
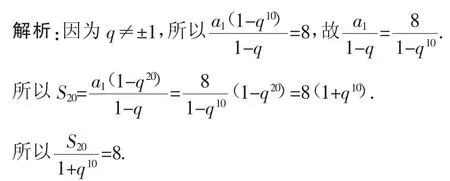
運用數形結合解決一些運算問題的關鍵在于對運算式中的幾何意義進行充分的挖掘.
例5若實數x,y 滿足x2+y2-2x-4=0,則u=2x+y 的最大值為多少?
解析:對此題的幾何意義進行充分挖掘,可知x2+y2-2x-4=0 表示圓心為(1,0)、半徑為的圓,u=2x+y 即2x+y-u=0 表示斜率是-2 的直線,而且圓與直線存在公共點,則圓心至直線的距離應滿足,即|u-2|≤5,解得-3≤u≤7.故umax=7.
3.突出“思維”的作用
為了培養出學生又快又準的運算能力,教師還應在運算途徑上進行設計,運算途徑的探尋是建立在思維活動的基礎上的,因此,教師首先應突出思維活動在運算中的價值與意義并引導學生在運算過程中養成探求合理、簡捷的運算途徑的意識和習慣.
例6試求函數的值域.
分析:常用的求值域的方法在此題的求解中顯然都是不可行的,因此,教師在此題的教學中應引導學生開動腦筋,對有效的解題途徑進行思考與探求.
思路1:聯想斜率,則可看成點(2,-1)和圓x2+y2=1 上的點(cosx,sinx)連線的斜率,然后在數形結合思想的運用下進行解題,此題得以求解,雖令人欣喜,但以下方法卻在解題思路上表現得更加簡捷.
思路2:由的形式聯想asinx+bcosx=sin(x+θ),則有ycosx-sinx=2y+1,可得·sin(x+θ)=2y+1,即,則有即(2y+1)2≤y2+1,解得因此函數的值域為
例7直線l:3x-y+4=0 和圓D:x2+y2+2x=0 相交于點A 和點B,O 為坐標原點,試求△ABO 的面積.
分析:如圖1,若根據常規思路來解決此題,一般都會先求|AB|的長,再求點O 到AB 的距離,最后再求出△ABO 的面積.常規思路雖然一樣能令此題得解,但運算對于學生來說卻存在不小的難度.我們不妨換一種解題思路,設l 與y 軸相交于C點,則S△ABO=S△ACO-S△BCO,如此求解顯然簡便很多.
解:設A(x1,y1),B(x2,y2),直線l和y軸相交于點C(0,4).
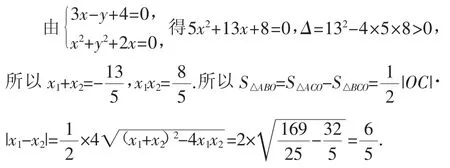

圖1
總之,學生數學運算能力的培養離不開運算的效率、合理、靈活、簡捷、正確等多方面的支撐.因此,教師首先應在思想上重視學生數學運算能力的培養,并在教學中進行針對性的引導,幫助學生養成良好的運算習慣及驗算習慣,使學生能夠在充分理解記憶公式、法則的基礎上獲得有意義的訓練.同時,教師還應關注到運算能力與數學其他能力之間的聯系與滲透關系,并引導學生在運算面前開展積極的思維,靈活運用數學思想方法尋求更加合理、簡捷的運算方法,只有這樣,學生才能在針對性的訓練中獲得數學運算能力及數學學習水平的不斷提升.

