對平面幾何問題求解入手點的思考

湖南省雙峰縣永豐中學 匡牡丹

在初中數學平面幾何問題的求解中，我們會遇到各種類型題，每類題都有不同的思路和解法.這些題型是否具有共同的本質？不同的解法之間是否有相通之處？到底應該從哪里下手來解決這些問題？該如何作輔助線？下面，介紹一下筆者對于解答平面幾何問題的思考與感悟.

一、從特殊角入手

在平面幾何題目的條件中，往往給出一些特殊角，如30°、45°、60°（或150°、120°、135°）、90°等，或者兩個角之間存在倍半關系，幾個角之間存在和差關系.如果出現90°角，可以構造直角三角形，運用勾股定理求解；如果出現60°角，可以與其他條件相結合，構造等邊三角形等.

在這類問題的求解中，利用這些特殊角，通過添加輔助線，構造特殊三角形，常常可以快速找到簡潔的求解思路.

例1如圖1所示，在△ABC中，點D在邊AB上，且∠ACD=30°，∠BCD=90°.則

分析：本題中給了兩個特殊角∠ACD=30°，∠BCD=90°，因此可基于此構造特殊三角形求解.

圖1

圖2

方法1：如圖2所示，過點A作CD的垂線，交CD的延長線于點E.

在直角△ACE中，因為∠ACD=30°，所以AC=2AE.

在△ADE和△BCD中，∠AED=∠BCD=90°，∠ADE=∠BDC，所以所以，所以BC=3AE.

方法2：如圖3，過點D作DF垂直AC于點F.

圖3

二、從特殊邊入手

特殊邊或邊的關系主要有：勾股關系，即一個三角形兩邊的平方和等于第三邊的平方，進而可以得到直角三角形，利用直角三角形的有關性質，證明垂直關系.

邊的倍、半、和、差關系等.與倍半有關的定理有：“直角三角形中，30°角所對的直角邊等于斜邊的一半”“直角三角形中斜邊上的中線等于斜邊的一半”“三角形的中位線等于相應邊的一半”.

邊的相等關系.主要有：“等角對等邊”“平行四邊形的對邊相等”“軸對稱圖形的對應邊相等”等.此外，還可以運用全等三角形得到邊的相等關系.

解題中遇到與上述條件有關的問題時，首先應該想到應用這些關系，構造特殊圖形.例如，當我們看到角平分線時，應想到過角平分線上的已知點作垂直于角的兩邊的線段；當我們看到中點時，應想到添加輔助線，使兩中點所連線段成為某三角形的中位線.這樣，許多難題便迎刃而解.

例2已知：如圖4所示，在△ABC中，點M為AC邊的中點，點E為AB上一點，且AB=4AE，連接EM并延長交BC的延長線于點D.求證：BC=2CD.

分析：本題的條件中含有相等線段及比例線段，因此可通過構造平行線或三角形的中位線等進行求解.

方法1：如圖5，過點C作CF∥AB交DE于點F.

因為點M為AC的中點，所以AM=CM.

因為CF∥AB，所以∠BAC=∠MCF.又∠AME=∠CMF，AM=CM，所以，所以AE=CF.

因為AB=4AE，BE=AB-AE，所以BE=3AE，所以

因為BC=BD-CD，所以BC=2CD.

圖4

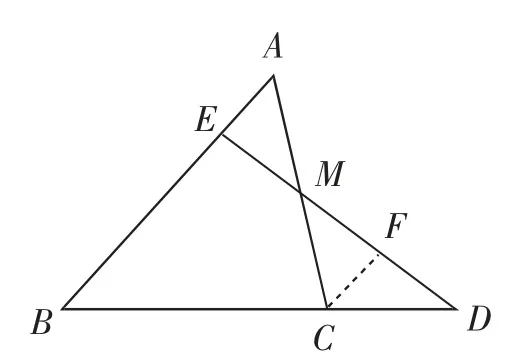
圖5

方法2：如圖6，過點C作CF∥DE交AB于點F.

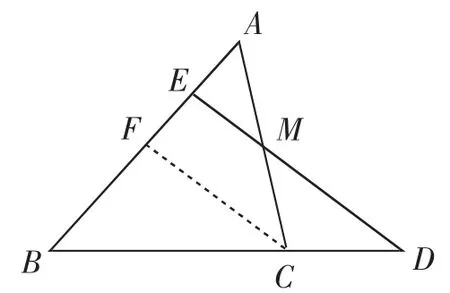
圖6

因為點M為AC的中點，所以AC=2AM，AF=2AE，AE=EF.

三、從特殊圖形入手

特殊的圖形主要包括正方形、長方形、等腰或等邊三角形、平行四邊形、菱形、圓等.例如，遇到涉及圓的問題，首先要想到構造已知直徑所對的圓周角；若已知切線，要想到連接圓心和切點等.熟練運用輔助線，化未知為已知，從而解決不能直接運用定理解決的平面幾何題.

例3如圖7所示，點C是以AB為直徑的圓O上一點，直線AC與過點B的切線相交于點D，點E是BD的中點，直線CE交直線AB于點F.

（1）求證：CF是圓O的切線；

（2）若ED=3，EF=5，求圓O的半徑.

分析：本題所給的條件中有直徑、有切線，據此構造垂直關系，可迅速找到解題的切入點.

（1）方法1：如圖8，連接CB、OC.

因為BD為圓O的切線，AB是圓O的直徑，所以∠ACB=90°，∠ABD=90°，∠BCD=90°.

因為∠BCD=90°，點E是BD的中點，所以CE=BE，所以∠BCE=∠CBE.又因為∠OCB=∠OBC，所以∠OBC+∠CBE=∠OCB+∠BCE=90°，所以OC⊥CF.

所以CF是圓O的切線.

圖7

圖8

方法2：如圖9所示，連接OE.

因為DB是圓O的切線，所以∠OBD=90°.

因為AB為圓O的直徑，所以BC ⊥AD，所以△BCD是直角三角形.

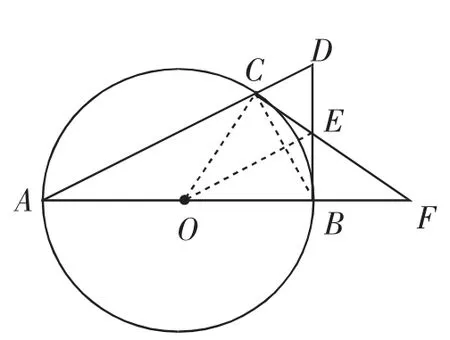
圖9

因為∠BCO=90°，點E為BD的中點，所以CE=BE.

在△OCE和△OBE中，OC=OB，OE為兩三角形的公共邊，CE=BE，所以所以∠OBE=∠OCD=90°，所以OC⊥CF.

所以CF是圓O的切線.

（2）解：因為CE=BE=DE=3，EF=5，所以CF=CE+EF=8.

因為∠ABD=90°，所以∠EBF=90°.又因為∠OCF=90°，所以∠EBF=∠OCF.又因為∠F=∠F，所以所以，所以OC=6，即圓O的半徑為6.

另外，需要注意的是，在某一問題中這些關系并不是獨立給出的，求解時要綜合運用這些特殊關系.

總之，在平面幾何問題的求解中，熟練運用特殊角、特殊邊、特殊圖形，快速聯想，熟記定理，適當添加輔助線，運用這些方法，即可快速找到問題的求解思路，從而順利、準確解決問題.