人教A版高中數學教材若干問題的商榷

徐小琴 張靜

對高中數學教材中函數定義、指數函數引例、任意角的表示、等差數列中的省略符號、幾何概型中轉盤表示等案例提出質疑，并提出若干編寫建議，意在引導學習者研讀教材、質疑教材、重構教材，從而激發學習者的科學精神、批判精神、創新精神。

人教A版? 數學教材? 編寫建議

教材的作用是系統的傳授知識。章建躍先生認為，教材的科學性體現在教材內容的準確性，包括素材的準確性，概念原理的正確性，問題解答正確無誤，用詞、術語、符號、圖表規范等[1]。教材是使得教學活動按照一定組織方式、邏輯順序、知識體系順利進行的載體，是教師的教與學生的學的聯系樞紐。教材不僅反映了課程改革的理念，也是指導教師課堂教學、學生學習的依據[2]。

一、函數定義不相稱

概念的定義是準確揭示一個概念的內涵和外延的邏輯方法，要使概念的定義合理、表述正確，應該遵循以下四條規則：第一，定義要相稱;第二，定義不得循環、反復;第三，定義要簡明;第四，定義一般不用否定形式[3]。仔細研讀高中數學教材函數的定義，發現其定義不科學，與概念定義規則中的“定義要相稱”相悖。

例1? 關于函數的定義，人教A版高中教材給出的定義為[4]： 設A，B是非空的數集，如果按照某種確定的對應關系f，使對于集合A中的任意一個數x，在集合B中都有唯一確定的數f（x）和它對應，那么就稱f：A→B為從集合A到集合B的一個函數（function），記作y=f（x），x∈A.

顯然，高中函數定義的是一元函數，而一元函數與二元函數、多元函數的外延并不相同，即定義項的外延大于了被定義項的外延，定義過寬。教材是教學實施的基本資料，是多數一線教師、學生知識獲取的主要來源，具有權威性與濃厚的信任色彩，定義應該做到精確、科學。函數定義建議更改為“那么就稱f：A→B為從集合A到集合B的一個一元函數（function）”。

二、指數函數引例不科學

例2 指數函數及其性質一節，在引入新課的環節設計了生物體碳14的含量P與死亡年數t之間的關系P=（■）■（t？叟0）與人口增長模式y=1.07x（x∈N*，x≤20）。從這二式的共同特征中抽象出了指數函數，進一步給出指數函數的定義，即函數y=ax，（a>0且a≠1）且叫作指數函數（exponential function），其中x是自變量，函數的定義域是R.

我們通過對定義的觀察發現，指數函數是有一定結構形式的，即y=ax其中自變量x作為指數，也就是說此處的指數若為2x，3x，■x…形式的都不是指數函數。基于此P=（■）■，就不是指數函數，正確的形式應改為P=[（■）■]■.

根據生物碳14的衰減規律來推斷生物死亡年數，我們不難發現此處自變量t∈Z，而指數函數y=ax中自變量x∈R，且形式應嚴格化為形式P=[（■）■]■.作為指數函數的引例應該要內容的準確和形式的規范，本例中的函數式嚴格意義上說不滿足指數函數定義，混淆學生對概念的理解。函數是對現實世界數量關系的抽象表示，函數本身不具有現實意義，需通過函數具有的性質并結合現實意義產生效力作用于現實世界。反之，實際生活的數據需要抽象出數，再借助函數表示，而抽象的過程不可省略。

三、任意角表示不規范

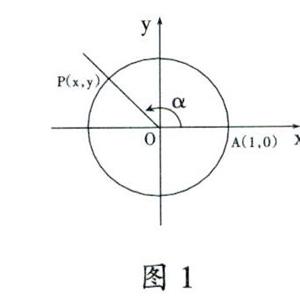
例3人教A版必修4第一章第2節任意角的三角函數“如圖，設？琢是一個任意角，它的終邊與單位圓交于點P（x，y）[5].”教材用圖1的？琢角表示任意角的方式是不規范的。

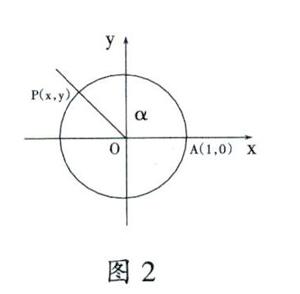
圖1的角？琢顯然是一個屬于（■，？仔）的鈍角，位于第二象限，以x軸正方向為始邊，以OP為終邊的角。其旋轉量及角度是固定的，具有特殊性。教材此處用這樣的一個特殊角來表示具有一般性的任意角顯然是不規范的。也有研究認為用圖2的方式表述任意角[6]，但是此處角的概念為圓弧所對的圓心角，即始邊與終邊的夾角，應將角標注在始邊與終邊之間，而標注在終邊之上僅能表示終邊與單位圓的交點，與交點P重復，與任意角的表述也大相徑庭。因此，筆者認為在表述任意角時去掉旋轉量，僅標注角？琢，既能充分表示角的任意性，還能讓學習者充分想象角的正負性（旋轉方向順時針或逆時針）。角的始邊與軸正方向重合，旋轉方向決定角的正負，終邊為OP。

四、等差數列省略符號意難測

例4 人教A版高中數學教材必修5等差數列一節習題2.2（A組），教材40頁第5題，給出某種昆蟲爬行速度的記錄，如下表所示[7]。

問題需要學生建立等差數列的模型，表示甲蟲爬行距離與時間之間的關系。

根據已有數據難以確定甲蟲的爬行距離與時間之間滿足等差數列的定義，因為省略號部分的運動情況不得而知，或許單位時間內甲蟲的爬行距離逐漸縮短，亦或甲蟲某個時間段停滯不前。

省略號的使用是判定數列是否為等差數列的陷阱。省略號省去的部分未必按照前面的規律傳遞下去，此時省略號不具有傳遞性。因此，筆者建議在表述等差數列時，一種是窮舉，即將數列每一項表示出來，如數列1，3，5，7，9，11，13，15。另一種是將等差數列的通項寫出，如數列1，3，5，7，9，…，2n-1，…

五、幾何概型轉盤意義模糊

例5 人教A版高中數學教材必修3第135頁幾何概型。圖3中有兩個轉盤，甲乙兩人玩轉盤游戲。規定當指針指向B區域時，甲獲勝，否則乙獲勝。在兩種情況下分別求甲獲勝的概率是多少[8]？

圖3中轉盤分為B，N兩個區域，其中轉盤分區規則、比例并未標注。如第一個轉盤未注明小區域N，B的相同，大區域的N，B也相同。第二個轉盤未注明轉盤每個區域均勻劃分。教材用“顯然”兩字得到區域的劃分比例實屬不易。建議在問題中注明轉盤劃分規則。本題轉盤指針指向區域的概率本質為指針指向不同區域圓心角的范圍。與區域面積或弧長、指針長度非本質聯系。本題的轉盤改為三角形、正方形、梯形等，其區域面積或弧長之比可能發生變化，而圓心角之比不變，此題結果不變。

參考文獻

[1]中國教育學會.如何在教材編寫中落實核心素養？[EB/OL].[2017-02-22].http：//www.sohu.com/a/126953497_387107.

[2] 嚴卿，胡典順.中國和日本初中數學教材中問題提出的比較研究[J].數學教育學報，2016（02）.

[3] 翁凱慶.數學教育概論[M].成都：四川大學出版社，2007.

[4] 劉紹學，等.普通高中課程標準實驗教科書數學必修1（A版）[M].北京：人民教育出版社，2007.

[5] 劉紹學，等.普通高中課程標準實驗教科書數學必修4（A版）[M].北京：人民教育出版社，2007.

[6] 王佩，趙思林.對人教A版高中數學教材中幾個問題的商榷[J].教學與管理，2018（02）.

[7] 劉紹學，等.普通高中課程標準實驗教科書數學必修5（A版）[M].北京：人民教育出版社，2007.

[8] 劉紹學，等.普通高中課程標準實驗教科書數學必修3（A版）[M].北京：人民教育出版社，2007.

【責任編輯? 郭振玲】