不同倒角半徑方柱繞流數值模擬研究

張志超，楊漢彬

(西南交通大學土木工程學院，四川成都 610036)

鈍體繞流(尤其是方形柱體繞流)是流體力學的經典問題之一。當流體以一定速度流經柱體結構時，流體會在結構后方產生規則的旋渦脫落，即卡門渦街現象。方形截面是典型的柱體截面形式之一，但工程中也存在方形帶倒角的截面形式，如各種大型橋梁的橋墩、高樁碼頭、高層建筑的立柱等。到目前為止，許多學者對方柱繞流問題進行了研究，Lyn等[1]對雷諾數Re=21400的方柱繞流流場特性進行了詳細的研究，給出了流動速度及其脈動量的分布，為數值模擬提供了事實依據和考核標準。秦浩等[2]對高雷諾數下方柱繞流問題進行了PIV(Particle Image Velocimetry)試驗和二維數值模擬，研究表明通過PIV試驗可準確觀測到方柱尾流的整個脈動流場且γ-Reθ模型對方柱繞流流場的模擬十分準確。付英男等[3]對方柱繞流進行了三維數值模擬，發現Re=100、300時方柱繞流存在三維特性，導致三維數值模擬計算的阻力系數和升力系數均小于二維計算結果。李雪健等[4]對方柱繞流進行了二維和三維數值模擬，結果發現三維數值模擬優于二維數值模擬且隨著雷諾數的增加，Cd的平均值增加而St先增大后減小。王遠成等[5]采用RNGk-ε湍流模型對方柱繞流流場進行了數值模擬，結果表明RNGk-ε湍流模型可以成功模擬繞方柱的不穩定，非定常和劇烈分離流動。朱夢楠等[6]對單個方柱及間距為1H，2H，3H的兩并列方柱的流動進行了數值模擬，研究發現當兩并列方柱之間的間距為2H時，方柱壁面處的升阻力會發生突變，間距為3H時，兩并列方柱繞流數值模擬的結果與單方柱繞流的結果類似。周強等[7]對高雷諾數下方柱繞流進行了三維數值模擬，結果表明：雷諾數為22 000下方柱尾流區回轉長度為1.37倍方柱寬帶，St為0.121，脈動升力系數為1.40，展向長度取8倍方柱寬帶可更準確地獲得三維湍流特性；沈立龍等[8]等人對亞臨界區圓柱和方柱繞流進行了數值模擬，發現同一雷諾數下圓柱繞流阻力系數較方柱繞流阻力系數要小，但圓柱的Strouhal數較方柱的要高，單圓柱和單方柱繞流生成的旋渦脫落周期不同，方柱的偏大，二者的旋渦脫落特性與流場運動具有相似特性。圓柱的分離點隨著雷諾數的增大而逐漸向柱后方推移，方柱的分離點則固定在柱前兩個棱角位置。雖然之前對方柱繞流問題進行了很多研究，但對于帶倒角方柱的研究卻很少，杜明倩等[9]采用數值模擬的方法對不同倒角半徑下方柱繞流進行了二維數值模擬，研究發現增加倒角半徑會改變方柱的分離點，使尾流區長度增加，旋渦尺度減小，柱體截面越接近圓形，斯托羅哈數會逐漸增大。Kumar等[10]使用粒子圖像流速測量技術(PIV)，研究了不同倒角半徑的流場特性，發現當倒角半徑越大時，尾流附近旋渦脫落越均勻。

本文運用CFD軟件、基于k-ωSST模型對亞臨界區Re=22000的單方柱和倒角半徑為0.15D、0.25D和0.35D的方柱進行了三維數值模擬，計算得到這幾種情況下的升阻力系數、斯特羅哈數等重要動力學參數，并對圓柱、方柱和帶倒角方柱繞流機制進行了分析。

1 控制方程與建模

1.1 控制方程

不可壓縮粘性流體的運動可用Navier-Stokes方程來描述，連續性方程與動量方程分別為：

式中：ui，uj為速度分量；p為壓力；ρ為流體的密度；v為流體的動力粘性系數。

對于湍流情況，本文采用k-ωSST模型，該模型綜合了k-ω模型在近壁區計算的優點和k-ε模型在遠場計算的優點，將k-ω模型和標準k-ε模型都乘以一個混合函數后再相加就得到這個模型。在近壁區，混合函數的值等于1，因此在近壁區等價于k-ω模型。在遠離壁面的區域混合函數的值則等于0，因此自動轉換為標準k-ε模型。與標準k-ω模型相比，k-ωSST模型中增加了橫向耗散導數項，同時在湍流粘度定義中考慮了湍流剪切應力的輸運過程，模型中使用的湍流常數也有所不同。這些特點使得k-ωSST模型的適用范圍更廣，如可以用于帶逆壓梯度的流動計算、翼型計算、跨音速激波計算等。模型方程如下：

(3)

(4)

式中：k為湍流動能，ω為湍流比耗散率，σω2=0.856，β*=0.09，混合函數`定義如下：

(5)

(6)

式中：y表示距離壁面的距離，CDkω代表比耗散率輸運方程中交錯擴散項的正值部分，渦粘系數定義為

(7)

式中：a1=0.31，Ω為渦量，混合函數F2定義如下：

(8)

模型中常數的取值為OpenFOAM中的默認值。

1.2 參數定義

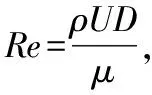
1.3 邊界條件和初始條件設置

計算流場的邊界條件和初始條件設置如下：

初始條件：初始設定一個從左向右的速度場，u=U0=0.22m/s，v=0，w=0；其中，u、v和w分別為x、y和z方向的速度，方柱邊長D=0.1m。

邊界條件：來流方向為均勻流速U0，出口為自由出流，方柱采用無滑移固壁邊界，其余邊界采用對稱邊界(圖1)。

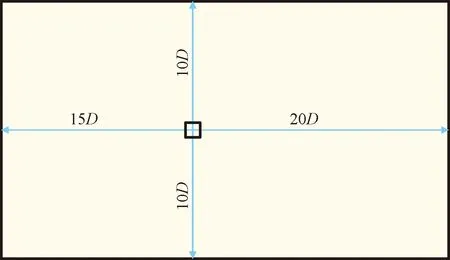
(a)XY方向計算域示意

(b)Z方向計算域示意

網格劃分采用六面體結構化網格，方柱壁面處y+取20，具體網格劃分如圖2所示。

(a)方柱

(b)倒角0.15D

(c)倒角0.25D

(d)倒角0.35D

2 計算結果分析

2.1 升阻力系數

圖3為利用OpenFOAM軟件模擬Re為22 000時方柱和倒角半徑為0.15D，0.25D和0.35D方柱阻力系數Cd及升力系數Cl隨時間t變化。

由圖3(a)可以看出，單方柱的阻力系數和升力系數在20s附近開始穩定，阻力系數穩定在2.12，升力系數在-1.92到1.92之間波動。當倒角半徑增大到0.15D時，方柱的升力系數和阻力系數都開始減小且阻力系數降低約46 %，而后當倒角半徑繼續增加時，方柱的阻力系數繼續減小，升力系數變化不大，當倒角半徑為0.35D時，阻力系數相對于倒角半徑為0.25D時無明顯變化，但升力系數卻開始增大。

表1為三維計算結果與實驗及以往文獻結果的對比，結果顯示，Re=22000時的模擬結果能很好的與參考文獻中數據相吻合，即說明本文模擬結果的正確性。

2.2 斯托羅哈數

斯托羅哈數又被稱為渦脫落的無量綱頻率。根據模擬所得結果繪制了Re=22000時單方柱和倒角半徑為0.15D、0.25D和0.35D方柱繞流的St隨倒角半徑的變化曲線如圖4所示。

(a)方柱

(b)倒角半徑0.15D

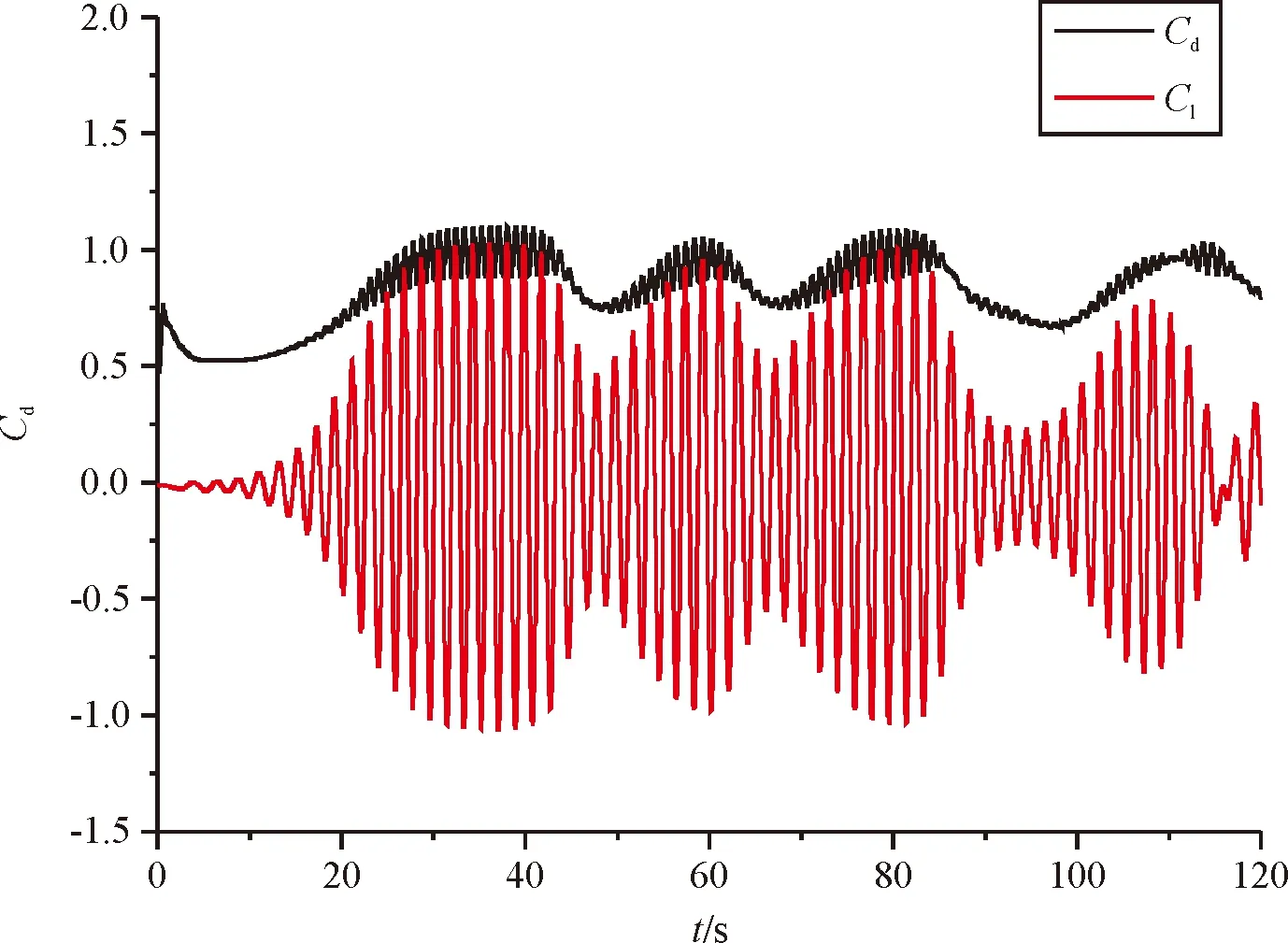
(c)倒角半徑0.25D

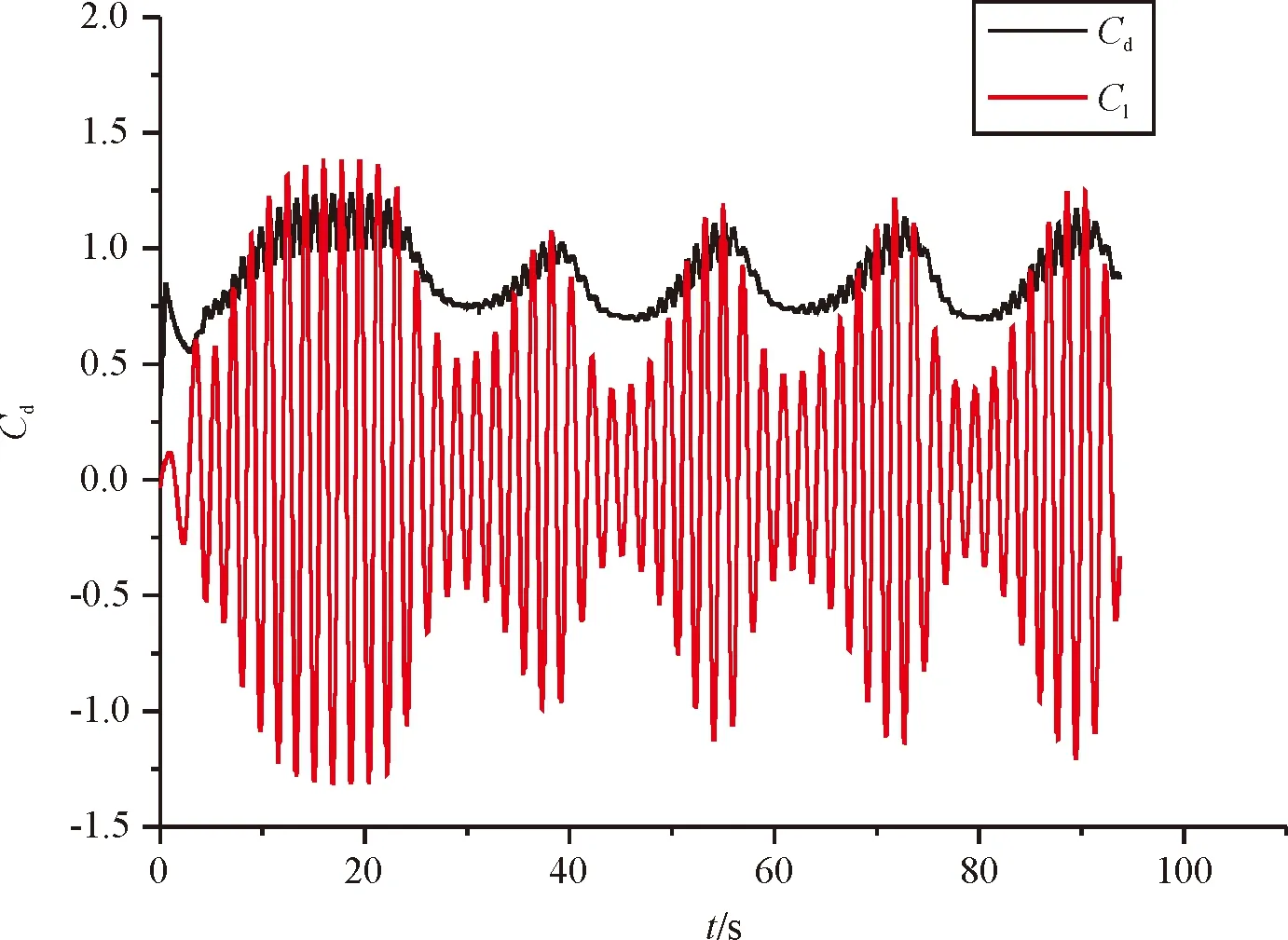
(d)倒角半徑0.35D

由上圖可知，單方柱的St為0.124，當倒角半徑增大到0.15D時，St以較快速度增大到0.212，當倒角半徑繼續增大時，St的增速變得平緩，說明方柱增加倒角后，旋渦脫落頻率

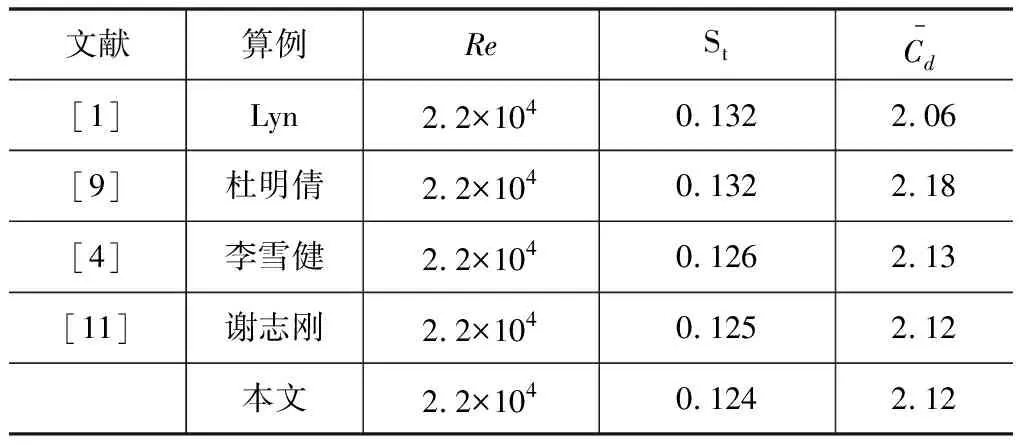
表1 Re=22 000時單方柱繞流模擬計算結果

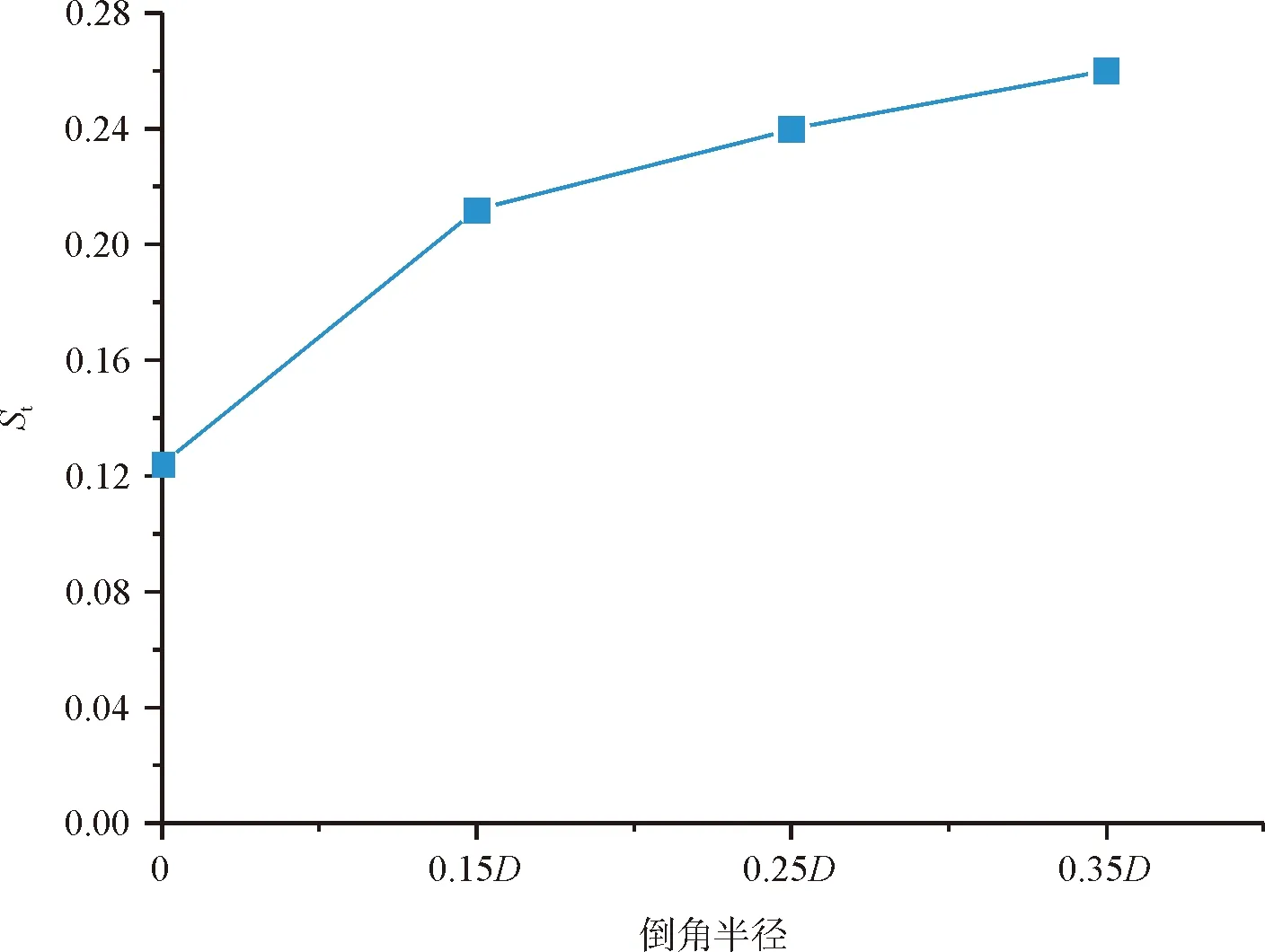
圖4 方柱繞流的斯托羅哈數隨倒角半徑變化曲線

會加快，脈動更強，這也與文獻[9]中的結果相一致。

2.3 三維渦量圖

方柱及倒角半徑為0.15D、0.25D和0.35D方柱的三維渦量圖如圖5所示。

(a)方柱

(b)倒角半徑0.15D

(c)倒角半徑0.25D

(d)倒角半徑0.35D

從上圖可以看出，由于方柱具有固定的分離角，其旋渦脫落在高度方向一致，而帶倒角方柱具有明顯的胞體結構，呈現明顯的三維特征。由于胞體結構的存在說明其旋渦脫落的相關性較弱，這也是導致其阻力系數小于方柱的原因之一。

2.4 邊界層分離

亞臨界區雷諾數下方柱繞流邊界層分離為層流分離，且邊界層內液體運動時會伴有能量損失，本次模擬的方柱雷諾數Re=22000，正好處于亞臨界區。對于圓柱見圖6(a)，隨著雷諾數的增大，分離點會逐漸向后推移。在壓強最大的P點至柱上下A、B兩點的邊界層內液流處于加速減壓狀態，在A、B兩點時壓強最小，流速最大，在這兩點之后液流處于減速增壓狀態，當動能減小至零無法提供壓能時，完成分離。對于方柱見圖6(b)分離點固定在柱前的兩個棱角位置。而對于帶倒角方柱見圖6(c)分離點則相對復雜，其分離點介于圓柱和方柱之間。

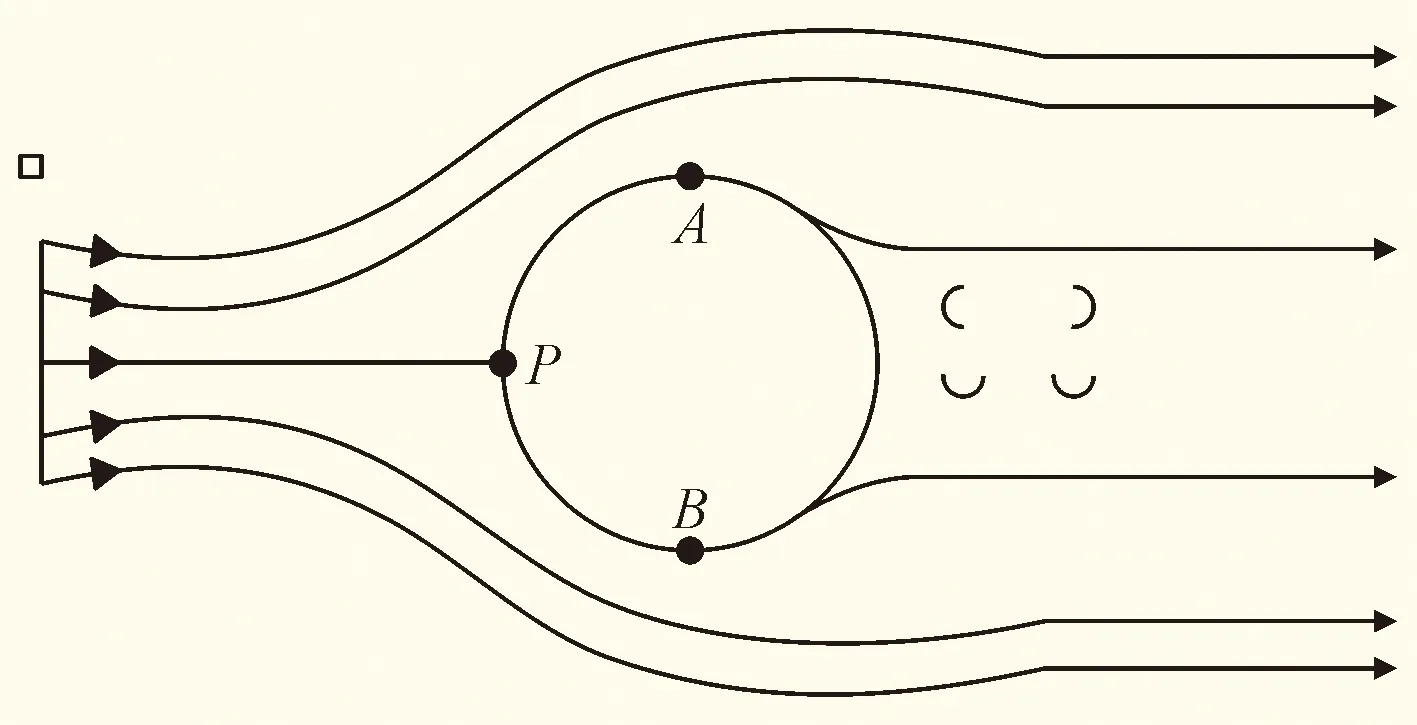
(a)圓柱

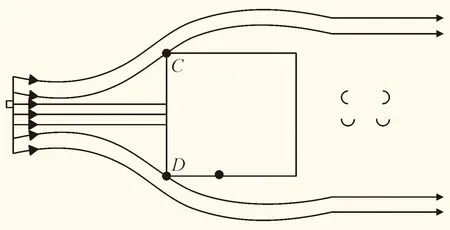
(b)方柱

(c)帶倒角方柱

3 結論

本文運用OpenFOAM軟件，通過對亞臨界區Re=22000下單方柱和倒角半徑為0.15D、0.25D和0.35D的方柱進行了數值模擬，得出以下結論：

(1)Re=22000時，單方柱的升力系數和阻力系數最大，隨著倒角半徑的增加，升阻力系數會減小，但當倒角半徑為0.35D時，升力系數相對于倒角半徑半徑為0.15D和0.25D時會增加，但始終小于方柱的升力系數。

(2)帶倒角方柱的三維數值模擬會出現胞體結構，呈現明顯的三維特性，柱體高度方向旋渦脫落的相關性較弱。

(3)在一定范圍內，帶倒角方柱的斯托羅哈數會隨著倒角半徑的增大而逐漸增大。

(4)單方柱繞流存在固定的分離點，即柱前兩個棱角的位置，當方柱出現倒角后，方柱的分離點發生改變，不再固定在之前的棱角位置，而是介于圓柱和方柱之間。隨著倒角半徑的增大，帶倒角方柱的流動特性越來越近似于圓柱。