基于TMD的鈍角風嘴鋼箱梁渦激振動控制研究
曾要爭, 喻 梅
(1.重慶市交通規劃勘察設計院, 重慶 400000;2.重慶交通大學山區橋梁結構與材料教育部工程研究中心, 重慶 400000)
來流氣流遇到鈍體結構時會發生分離和再附進而產生漩渦的脫落,當漩渦脫落頻率與結構振動頻率一致時,結構就會發生渦激振動,它是一種具有自激和限幅雙重性質的風致振動,大多發生在常見風速下[1]。目前世界上很多橋梁,如中國香港昂船洲大橋[2]、丹麥Great Belt East橋[3]、俄羅斯伏爾加河大橋等均出現過渦振現象。長時間的振動也會引起結構的疲勞破壞,同時渦激振動也會影響橋上行人的舒適度和行車安全[4],因此,進行橋梁結構渦振性能試驗及抑振措施研究具有重要的工程借鑒意義。
渦振的抑制措施主要有結構措施、機械措施和氣動措施三類[5]。結構措施不能從根源上解決渦激振動的問題。氣動措施是通過改變橋梁主梁的氣動外形進而優化主梁的渦振性能,但需要通過反復試驗找出渦振的影響因素。機械措施則是通過布置調制阻尼器抑制結構振動。Fujino Y等[6]在1985年討論了TMD抑制橋塔的馳振,較早地介紹了TMD在橋梁上的應用。顧明等[7]針對大跨度橋梁的抖振采用TMD進行控制,并提出了TMD的最優阻尼比等參數。陳艾榮等[8]在試驗室完成了應用TMD對斜拉橋豎向抖振控制研究。氣動優化方案基本上是通過風洞試驗完成的[9],而TMD制振措施的部分參數可以通過程序計算得到,比如:最優阻尼比、減振率、自振頻率等[10]。流線型鋼箱梁截面接近流線型,常被應用于大跨度橋梁。實際中,由于各種因素的限制,存在風嘴短而鈍的流線型鋼箱梁斷面,且考慮人行道欄桿、檢修車軌道等作用后,會進一步弱化主梁的渦振性能。
本文以流線型鋼箱梁懸索橋為背景,通過1∶50節段模型風洞試驗研究其渦振性能,基于TMD抑振機理,分析了TMD的相關參數給出最優方案,對以后同類橋梁渦振控制有一定的指導和借鑒意義。
1 TMD振動控制機理
機械措施控制渦激共振主要包括TMD(被動振動控制),AMD(主動振動控制)和HMD(混合振動控制)。TMD(Tuned Mass Damper),意思為調諧質量阻尼器,也被稱為諧波吸收器,是安裝在結構上,以減少機械振動振幅的裝置。其應用可預防結構振動引起行人的不適、損傷或失效。它們經常用于電力傳輸、汽車、橋梁和其他建筑物等。TMD的作用機理如圖1,它由一個小質量M2通過剛度為K2的彈簧連接在彈簧剛度為Ke的主結構質量Me。在簡諧荷載f(t)的作用下,小質量M2可以通過自身的振動來吸收能量,從而減小主結構質量Me的振動,這樣的結構極大增加了阻尼。
(1)

圖1 主結構-TMD模型
由于渦激振動時橋梁受到了類似諧和激勵,故在計算過程中把f(t)假設為諧和激勵。
令f(t)=Peiωt,x1=A1eiωt,x2=A2eiωt,有:
(2)
式中:H(ω)=G-1(ω);G(ω)=[k-mω2+icω]。

(3)
H(ω)=ke-meω2+ic1ω
(4)
TMD參數包括阻尼器與結構的廣義質量之比、頻率之比及阻尼比,其參數的選取對制振效果至關重要。
對于調諧式阻尼器的頻率之比、阻尼比可以按照下面公式計算:
(5)
(6)
式中:ω0為阻尼器的圓頻率;ζ0為阻尼比;ωs為受控振型圓頻率。
μ為阻尼器與結構受控振型的廣義質量比,按下式計算:
(7)
式中:L為橋梁跨長或塔高;m0為阻尼器質量;m(x)為橋梁單位長度質量(kg/m);Φi(x)為受控振型值;x0為阻尼器安裝位置;Φi(x0)為阻尼器按照位置相應于Φi(x)的振型值。
2 流線型鋼箱主梁渦振控制
某主跨410 m的單主纜懸索橋,橋塔采用混凝土結構,主梁采用流線型鋼箱梁。橋寬36.4 m,高3.5 m,主梁寬高比為10.4,風嘴截面夾角為79.6 °,風嘴寬0.6 m,風嘴短而鈍(圖2)。橋梁結構的主要振型以及對應的頻率見表1。
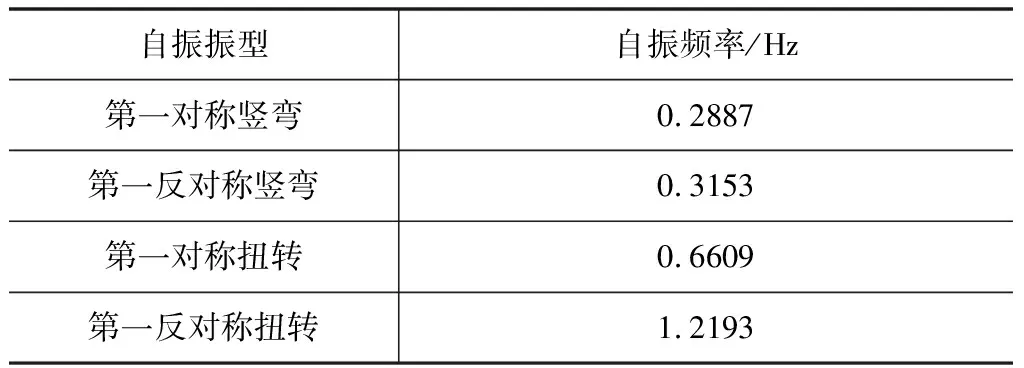
表1 橋梁動力特性

圖2 主梁斷面(單位:m)
2.1 節段試驗模型試驗及結果
為研究該橋的渦振性能,制作主梁的節段模型進行風洞試驗。節段模型的幾何縮尺比為1∶50,模型長2.095 m,寬0.728 m,高0.070 m,且風洞試驗阻塞比小于5 %。模型采用優質木材和塑料板制作,人行道欄桿等附屬構件均采用高級塑料板由數控雕刻機制作而成。試驗在均勻流場中進行,節段模型由8根拉伸彈簧懸掛在支架上,且模型兩端設置端板(圖3),相關試驗參數見表2。根據JTG/T D60-01-2004《公路橋梁抗風設計規范》的有關規定,按一階對稱豎彎計算的渦振振幅允許值為:0.1386 m。

圖3 節段模型

參數實橋模型第一階對稱豎彎頻率/Hz0.28873.59第一階對稱扭轉頻率/Hz0.66099.53質量/(kg·m-1)2506010.47質量慣性矩/(kg·m2·m-1)23762211.023
本文主要分析阻尼比為0.3 %,攻角為±5 °、±3 °和0 °時主梁的渦振性能。
成橋狀態下,主梁在-5 °、-3 °攻角時,未出現明顯的渦激振動(未列出數據)。如圖4,0 °攻角時,主梁出現了1個豎向渦振區;+3 °攻角時,主梁出現了2個豎向渦振區,其中第2個豎向渦振區的主梁豎向最大振幅為438 mm,遠大于規范允許值。+5 °攻角時,出現了2個豎向渦振區,其中,最大渦振振幅對應的風速均在30 m/s左右,與該橋主梁設計基準風速30.1 m/s較接近。因此,本文重點關注風速小于主梁高度處設計基準風速時主梁的渦振性能,即攻角3 °和0 °時的主梁渦振性能。
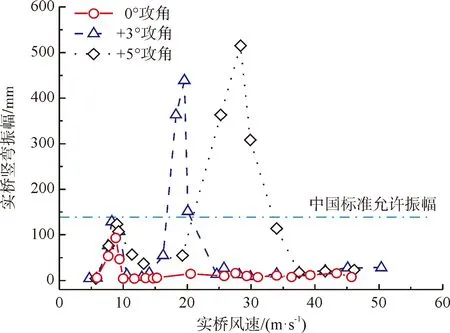
圖4 主梁斷面豎向渦振響應
2.2 TMD振動控制與參數分析
為了取得最大減振率,TMD一般布置在振型最大處。TMD質量,在橋跨范圍內按兩個截面布置,每個截面分成一個到兩個箱布置,對于第一階豎向振型布置1處,每處Mt,M/2×2(每處兩個箱各1)×1(處)=Mt。對于M和T的取值見表3。
試驗時考慮實橋阻尼比為0.1 %、0.3 %、0.5 %和0.8 %。行程比為安裝TMD后的橋梁振動振幅與TMD的振動振幅的比值;減振率為安裝TMD后,與未裝TMD相比振動振幅的減小的比例。TMD的質量分別取為10 t、30 t、40 t、50 t、60 t、70 t和80 t情況;另外還考慮一些特殊情況,比如質量比為0.4 %和0.5 %的情況。

表3 TMD不同質量時的最優參數
圖5、圖6給出了不同質量比時的行程比和減振比結果,可知,TMD的阻尼比對制振效果影響顯著,取最優阻尼比時效果最好,阻尼比為15 %時效果最差。但TMD取最優阻尼比行程過大,不利于TMD在工程中的應用。盡管10 %的阻尼比比最優阻尼比制振效果有所減弱,但仍然滿足要求,且TMD的行程始終;阻尼比大于15 %時,制振效率下降。綜合考慮,TMD取10 %左右最為合適。
對于第一階豎向振型,盡管這一振型的TMD的總質量為10 t時,便可以符合要求,但為了安全,建議取20 t。表4給出了具體的TMD參數,表5給出了對應的制振結果,從中可以看出TMD制振效果良好,采用TMD制振方案后,主梁渦振振幅滿足中國規范允許值。
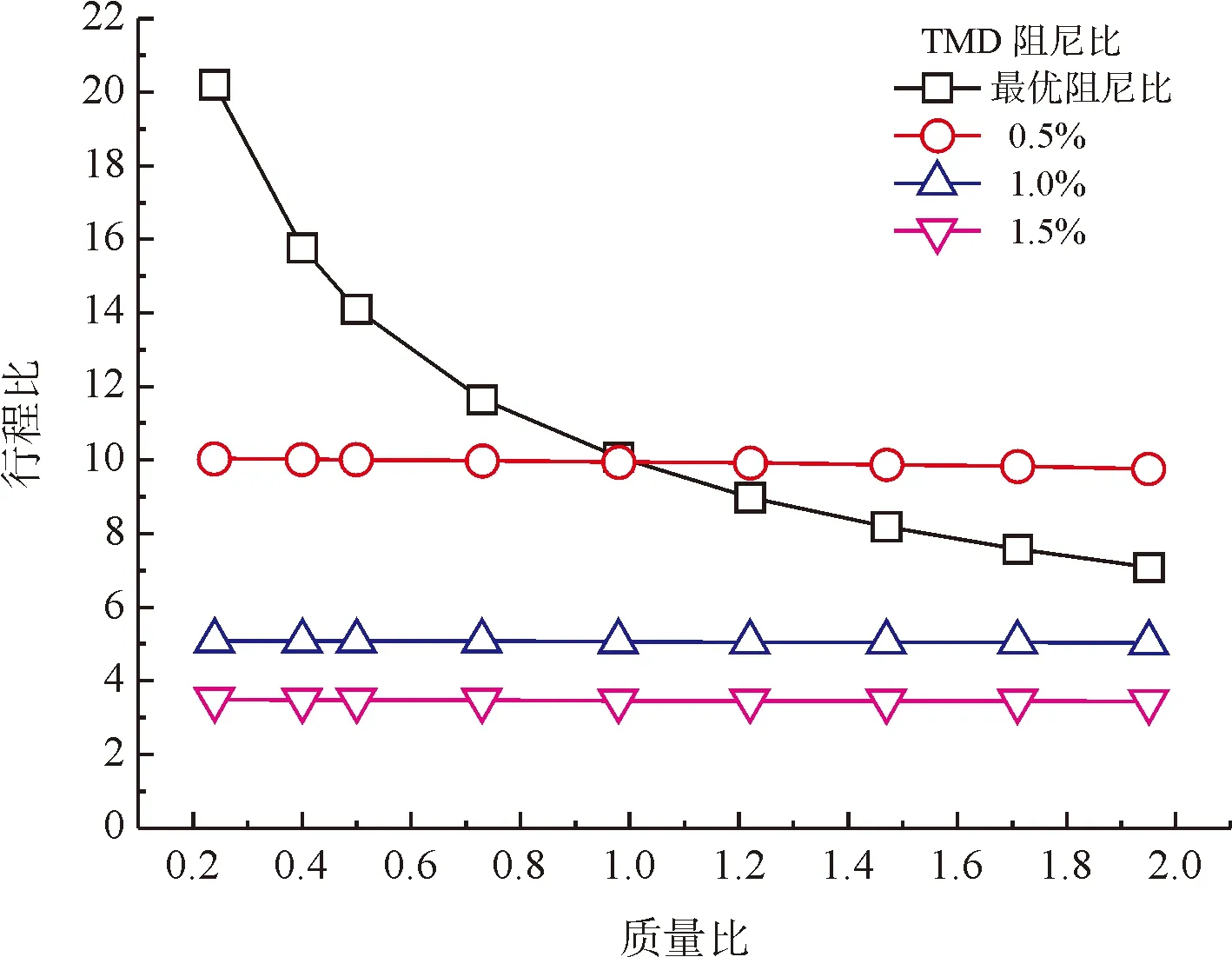
圖5 TMD阻尼比對行程比的影響

表4 主梁TMD控制參數建議

表5 TMD制振方案對于主梁豎向渦振的抑制效果
2.3 舒適度評價
對于舒適度只需考慮風速小于10 m/s時發生的渦激共振,因此主要考慮豎向迪克曼指標的K值和杰奈威指標[11]對舒適度進行評價,其具體定義見文獻[11]。
表6和表7對比了原設計方案和TMD制振方案。對于原方案,主梁會出現很大的渦激共振,使行人非常不舒服,并且感覺疲勞,難以忍受。而加TMD后因為主梁渦激共振帶來的不適感明顯減少。因此,TMD措施可以抑制渦振,并且滿足行人舒適度的要求。
其中,疲勞:一般人對振動過分疲勞的上限;短期忍:能忍受短期振動。
3 結論
通過節段模型風洞試驗對帶有短而鈍風嘴的流線型鋼箱梁的渦振性能進行了測試,提出采用TMD制振方案抑制主梁的豎向渦振,得出如下結論:

(a)主梁阻尼比0.1%

(b)主梁阻尼比0.3%

(c)主梁阻尼比0.5%

(d)主梁阻尼比0.8%

風攻角豎向頻率/Hz原設計方案機械控制方案(TMD)最大位移/mmK值迪克曼指標最大位移/mmK值迪克曼指標0°0.288793.2515.5疲勞17.853.0短期忍3°0.288712821.3疲勞24.504.08短期忍

表7 優化與不優化的舒適度(杰奈威指標VG)
(1)流線型鋼主梁在0 °、+3 °及+5 °攻角下出現了明顯的豎向渦激振動,且最大振幅大于中國規范允許值;但重點關注風速小于主梁高度處設計基準風速時主梁的渦振性能,即風攻角3 °和0 °時的主梁渦振性能。
(2)針對主梁的豎向渦激共振振幅大于容許值,研究了TMD制振方案來抑制渦激共振,抑制效果良好。
(3)利用迪克曼指標和杰奈威指標評價了原方案和加TMD后主梁的舒適度,表明TMD制振方案不僅可以抑制主梁豎向渦振同時可以滿足舒適度要求。

