非平凡樹的最小路分解數
(長江大學信息與數學學院,湖北 荊州 434023) (湖北省洪湖市第一高級中學,湖北 洪湖 433200)
筆者討論的圖均為沒有重邊的簡單圖。對圖G,用|V(G)|和|E(G)|分別表示圖G的頂點數和邊數。一條從x0到xk的路徑P表示為P=x0x1…xk,其中Pxi=x0…xi,xiP=xi…xk。用Pk表示圖中包含k個頂點的路徑,其長度為k-1。如果圖G的邊集E(G)可以分解為若干邊不重合的子圖H時,就稱G有H分解,若H={P1,P2,…,Pk},則稱圖G有路分解,令p(G)=min{||:是G的一個路分解},即圖G的路分解的最小條數,設是G的一個路分解,若||=p(G),則稱是圖G的一個最小路分解。設v是圖G的一個點,dG(v)表示圖G中與點v相關聯的邊的條數,稱為點v的度。一個連通且沒有圈的圖稱為樹,通常用字母T來表示樹。其中僅有一個點構成的樹稱為平凡樹,否則稱為非平凡樹。樹T中度為1的點稱為懸掛點(葉子),通常用L(T)表示樹T中葉子的集合,與它相關聯的邊稱為懸掛邊。設x是任意的實數,[x]表示不超過x的最大整數,┌x┐表示不小于x的最小整數。所涉及的相關符號見參考文獻[1] 。
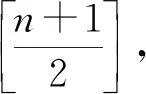
1 相關引理
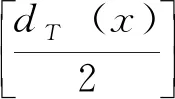
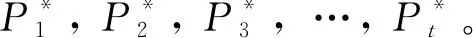
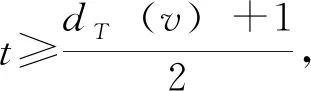
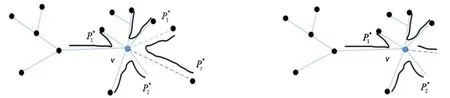
圖1 dT(v)為偶數 圖2 dT(v)為奇數
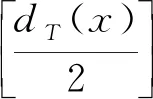
引理2設是樹T的一個最小路分解,?v∈V(T)。若dT(v)為偶數,則在中不存在以點v為端點的路徑;若dT(v)為奇數,則在中必存在以點v為端點的路徑。
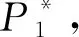
另一方面,當dT(v)為奇數時,假設中不存在以v為端點的路徑,那么過v點的每條路都會經過與v相關聯的2條邊,從而與v相關聯的邊數為偶數,這與dT(v)為奇數相矛盾。
引理3設T是一個樹,且T′=T-{u},其中u∈L(T),則有p(T)≥p(T′)。
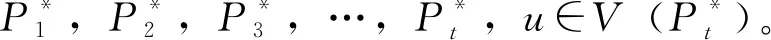
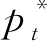
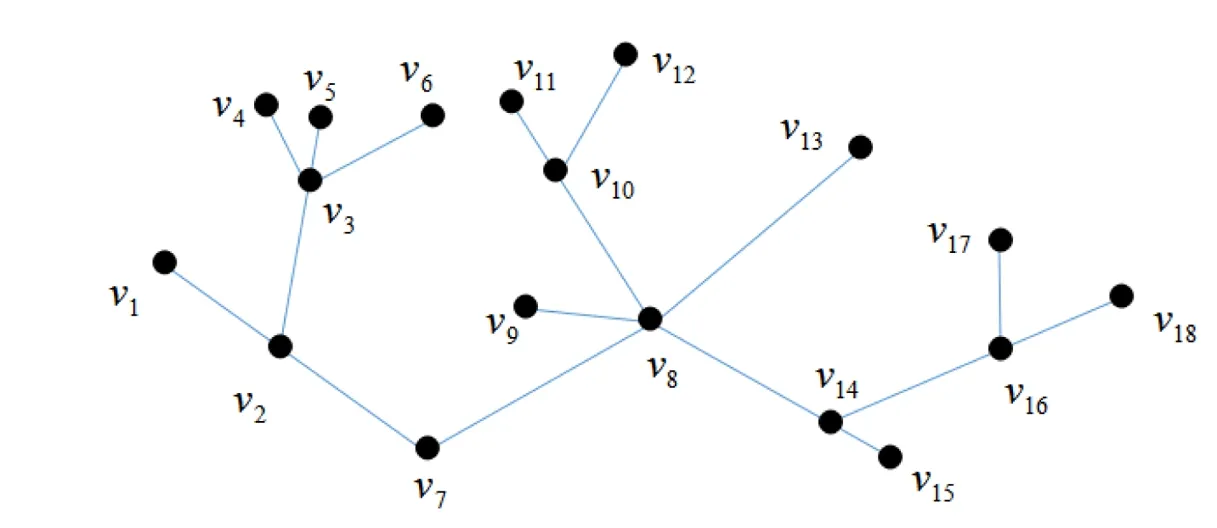
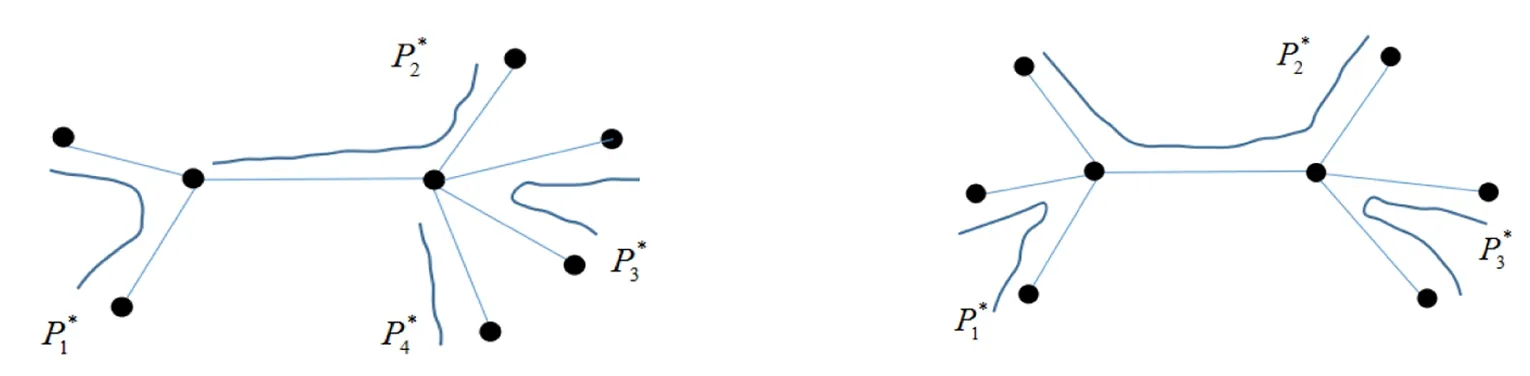
p(T′)≤t-1=p(T)-1 p(T′)≤t=p(T) 綜上所述p(T)≥p(T′)。 證明T是非平凡的,故|T|≥2。用數學歸納法證明。 當|T|=k時,不妨取u∈L(T),點u在T中的鄰點記為v。令T′=T-{u},則有|T′|=|T|-|{u}|=k-1 1)當dT′(v)為奇數時,由引理2,在T′的最小路分解中,必有一條路P∈是以v為端點,此時構造一條路徑P′使得P′=P+vu,則′=-P+P′是T的路分解。故有: p(T)≤|′| 2)當dT′(v)為偶數時,由引理2知,在T′的最小路分解中,不存在以v點為端點的路徑。設P∈是一條通過v的路徑,不妨令P={…wvt…},由P及u構造2條路徑則為T的路分解。可得: p(T)≤|′| 由引理3知,p(T)≥p(T′),當dT′(v)為偶數時,即dT(v)為奇數,則取等號不成立。 綜上即有: p(T′) 故: 例1某個樹T的結構如圖3,求樹T的最小路分解數。 由定理1易知在度為1和2的點上結果為0,故現只討論度大于2的點的情況。 =1+1+2+1+1+1+1=8 圖3 最小路分解數為8的樹 注1一個樹最小路分解的數目與該樹的葉子數無關。 不難看出,圖4和圖5中其葉子數目都是6,但是在圖4中最少分解路為4,而在圖5卻為3。由此得出,結論樹最小路分解的數目與該樹的葉子數無關。 圖4 最小路分解數為4的樹 圖5 最小路分解數為3的樹 研究了樹可分解路的最小條數,這一結論為一般連通圖中的路徑的研究奠定基礎,在圖論的結構理論研究中有著重要的意義。由樹的路分解,進一步可以研究樹的路因子理論,這將是以后的重點研究對象。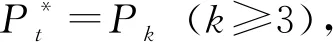
2 主要結論
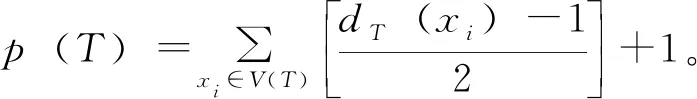
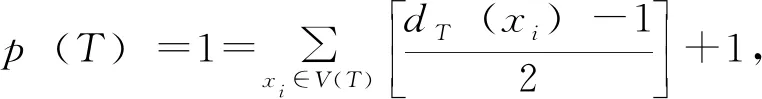
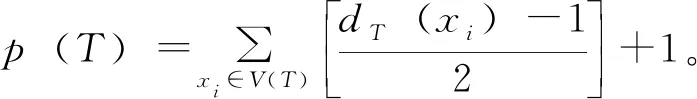
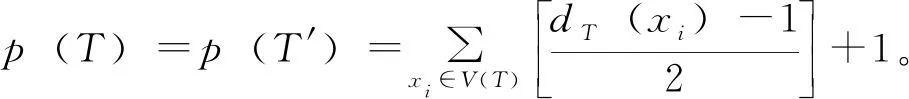
3 應用
4 結語

