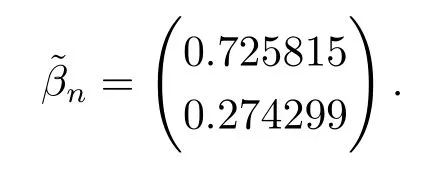長相依固定設計下部分線性EV 模型的小波估計的漸近性質
劉香, 胡宏昌, 余新新
(湖北師范大學數學與統計學學院, 湖北黃石435001)
1 引言
部分線性EV 模型如下

這里{yk,k=1,2,···,n} 是觀測值,β是一維未知參數,g(t) 是光滑的曲線, {tk} 為區間[0,1]內的序列.{εk,k=1,2,···,n} 表示隨機誤差, 變量{xk} 不能直接被觀測, 只能通過Xk=xk+uk來觀測, 其中{uk} 是測量誤差, 且假設{uk} 為已知獨立同分布的隨機變量, 而且對于每個k值, {uk} 與{εk,k=1,2,···,n} 都是相互獨立的.假設E(εi)=0, var(εi)=1 (即假定已知).則自協方差函數為

這里0<θ<1 是常數,L(t),t∈(0,∞) 是正的緩慢變化函數, 即
幾十年來, 部分線性EV 模型已經被廣泛研究, 文獻[1–4]用小波估計的方法研究了部分線性回歸模型, 在誤差序列{εk} 獨立同分布時, 得到估計量的大樣本性質; 若其誤差為鞅差序列, 如參考文獻[5], 則使用近鄰估計方法來研究了部分線性EV 模型.相依誤差的一個重要的特殊情況就是誤差為長相依的.這種情況會出現在經濟學, 時間序列分析和其他學科領域的運用中, 見文獻[6–8].使用小波估計對半參數模型的研究見文獻[3, 9].文獻[10]是對固定設計下的半參數回歸模型使用非參數權函數法和最小二乘法.在一定的正則性條件下, 文獻[11]中研究了部分線性模型中參數β和函數g(·) 的估計的弱相合性, 均方相合性和收斂速度, 得到了這些估計的漸近表示和漸近分布; 文獻[12]研究了長相依隨機設計下的部分線性EV 模型, 得到了參數估計量的漸近表示, 漸近分布和弱收斂速度.本文是在這些文獻的基礎上, 運用小波估計研究了固定設計下的參數估計量的漸近表示, 漸近分布和弱收斂速度.
2 小波估計
本節中, 我們使用小波方法估計未知參數和非參數.令Ai=[si?1,si]表示區間[0,1]的劃分區間, 且由(1.1) 式, 得到

假設Schwartz 空間Sl中存在尺度函數φ(x), 在伴隨Hilbert 空間中存在多分辨率分析Vm,它的再生核定義為將(2.3) 式看成一般部分線性回歸模型.首先, 假設β已知, 定義g(t) 的估計量為

然后, 通過最小化方法來定義小波估計量
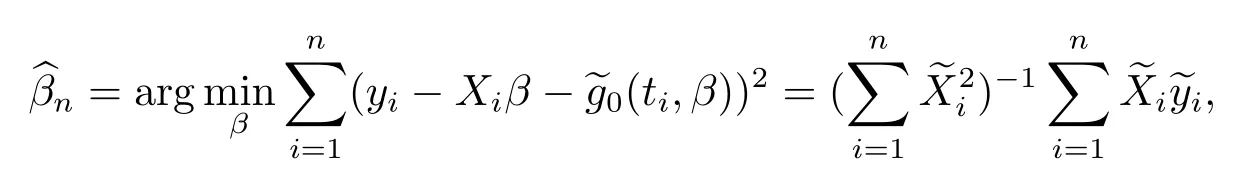
由于在線性回歸或在部分線性回歸中, 由測量誤差所導致的不一致性可由“衰減效應”所克服.因此使用以下修正的最小二乘估計量

最后, 定義g(t) 的小波估計量為

3 主要結果
為了獲得主要結果, 作如下假設條件
(1) 令xj=f(tj)+νj,j=1,2,···,n, 這里f(tj) 是區間[0,1]中的函數, 對于實數列{νi}, 有
(2)g(·),f(·)∈Hα(Sobolev 空間),α>1/2;
(3)g(·),f(·) 都是階數為γ>0 的Lipschitz 函數;
(4) 2m=O(n?1),0<θ 注1條件(2)–(4) 在小波估計中常被用到(見文獻[4,10,17,19]).條件(1) 是研究部分線性模型時常用到的條件, 但是本文條件與他們有所不同. (1)文獻[9,10,13]均對|νi|p(p≥2) 施加條件, 本文僅對|νi| 施加條件; (2)文獻[9,10,13]中對νi施加的條件較多, 本文對νi僅有一個條件; (3)雖然文獻[10,13]的條件及文獻[9]中的條件A1)i) 均可由本文中νi的條件(條件(1)) 推出(本文中νi的條件比文獻[10,13]的條件及文獻[9]中的條件1 強), 但本文中νi的條件推不出文獻[9]中的條件A1)ii).說明本文νi條件比文獻[9]中的條件A1) ii) 弱. 因此文獻[9]中條件A1)ii) 不成立. 注2與文獻[12]類似, 文獻[12]是隨機變量, 本文是固定設計. 定理1假設條件(1)–(4) 均成立, 則對任意的α≥3/2, 且有 假設定理1 的條件及結論成立, 則有以下推論, 其中推論1 和推論2 與文獻[12]中推論相同. 推論1若{ek,k=1,2,· · ·} 是獨立隨機變量,G(s)=s, 則對E|uk|4+2δ< ∞,有 推論2在定理1 的條件下, 若uk=0, 則 定理2若定理1 的條件成立, 則對λ/<θ, 且有 為了證明主要結果, 首先介紹一些有用的結論及引理. 首先介紹Hermite 秩的表示和Hermite 級數的一些基本結論.令e表示N(0,1) 上的隨機變量, 且G={G:E(G(e))=0,E(G2(e))<∞}, 則G是 構成了L2(R,Φ(s)) 中函數的完整正交系統, 并滿足E(Hl(e)Hq(e))=δlqq!. 對任意的G∈G, 令J(q)=EG(e)Hq(e).定義且為G的Hermite 秩.由于J(0)=E(G)=0, 故通常是正數. 令{ek,k=1,2,···,n} 和ρ(k) 如上所述,>0 為固定常數, 則以下結果成立[18]. (F2) 對任意Hermite 秩為<1/θ, 可測函數G∈L2(R,Φ(s)), 特別的, (F3) 對任意緩慢變化函數L(n) 而言, 有 (F4) {Hq(ei)} 是L2(R,Φ(s)) 中的一列隨機變量, 且滿足 引理1[3]假設條件(3) 成立, 則 引理2假設條件(1) 和(3) 成立, 則xi有界,有界, 且 證由于{νi} 是實數列,f(·) 是階數為γ> 0 的Lipschitz 函數, 故xj=f(tj)+νj,j=1,2,··· ,n有界.由和引理1(2), 有 引理3令則有 證為了證明此引理, 只需證明注意到 由Cr不等式及引理2, 有 由ui的獨立性得 由引理1 及ui的獨立性得 引理4[14]假設條件(1)–(4) 成立, 則 引理5[11]假設條件(4) 成立, 則對每個實數a1,a2,···,an, 下列分解成立 這里Tl1,Tl2滿足 引理6[13]令表示函數G∈G 的Hermite 秩,ai表示有界的非負實數, 則它的Hermite 秩也是, 且 引理7[15]若G(ei)∈G 的Hermite 秩是, 則 定理1 的證明對由引理2 進行如下分解 由引理6 及(F4) 有 由引理2 及(F4) 有 對Tn3求二階矩 由引理2 及(F2) 有 由引理6 及(F2) 有 由(5.3)–(5.4) 式可得 對Tn4求二階矩 由引理2 及(F2) 有 由引理6 及(F2) 有 由(5.6)–(5.7) 式可得 對Tn5求二階矩 由引理2 有 由引理2 及引理6 有 由(5.9)–(5.10) 式可得 由(F4) 有 對Tn7求二階矩 由(F2) 有 由(5.12) 式及(F2) 有 由(5.14)–(5.15) 式可得 對Tn8求二階矩 由(F2) 有 由(5.12) 式及(F2) 有 由(5.17)–(5.18) 式可得 對Tn9求二階矩 由引理2 有 由(5.12) 式及引理2 有 由(5.20)–(5.21) 式可得 對Tn10求二階矩 由(5.12) 式, 有 由(5.23)–(5.24) 式可得 由(5.12) 和Chebyshev 不等式可得 定理1 證畢. 推論1 的證明由(3.1) 和(5.28) 式, 有 因此由(5.29)–(5.30) 式得推論1 成立. 推論2 的證明由(3.1) 和(5.28) 式, 有 因為 且 因此由(5.31)–(5.32) 式得推論2 成立. 定理2 的證明 注意到 因為 所以有 從而 由上式和引理2 有 由引理6 和引理7 有 由引理1 有 因此由Markov 不等式和(F3) 可得 由引理1, 可得到 定理2 證畢. 為了對本文的證明結果做進一步的解釋和驗證, 選取2013 年5 月到2018 年8 月之間的全國居民消費價格指數, 城市居民消費價格指數和農村居民消費價格指數, 使用Mathmatic來做模擬應用(具體數值見東方財富網《中國居民消費價格指數》). 使用下述的式子 其中設全國居民消費價格指數為y, 城市居民消費價格指數和農村居民消費價格指數為矩陣X, 通過X, 由Mathmatic 算得 圖1: (t) 的散點圖 相對誤差H由下式算得 64 個數據中有55 個在0.05%以內,占總數的85.94%;有9 個在0.1%以內,占總數的14.06%,在一定程度上說明估計出的和(t) 是有效的.這個例子也直接說明了本文前面所證明的結論是正確的, 對于數據處理預測也有實際的作用. 具體計算的結果如下表1. 表1: 相對誤差表

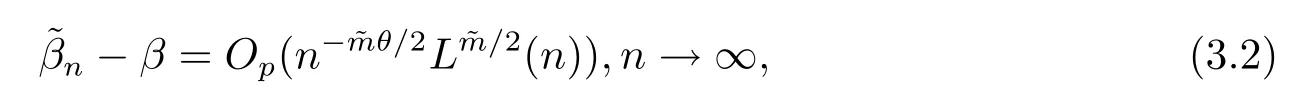
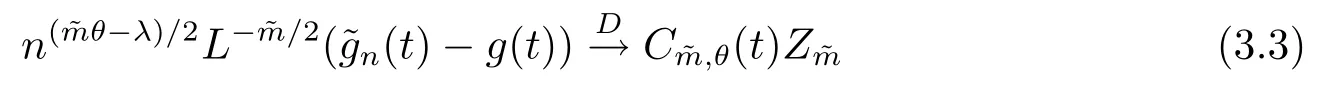

4 主要結果證明所需的引理



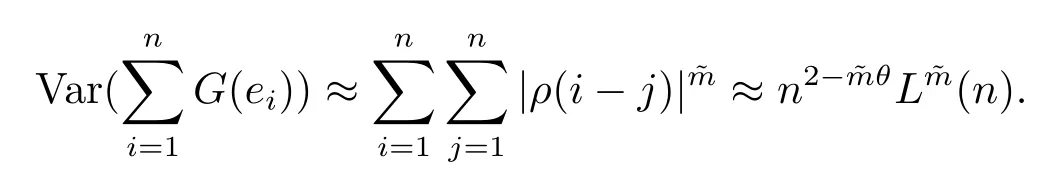




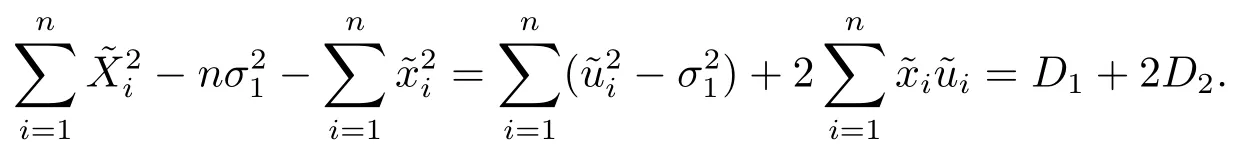
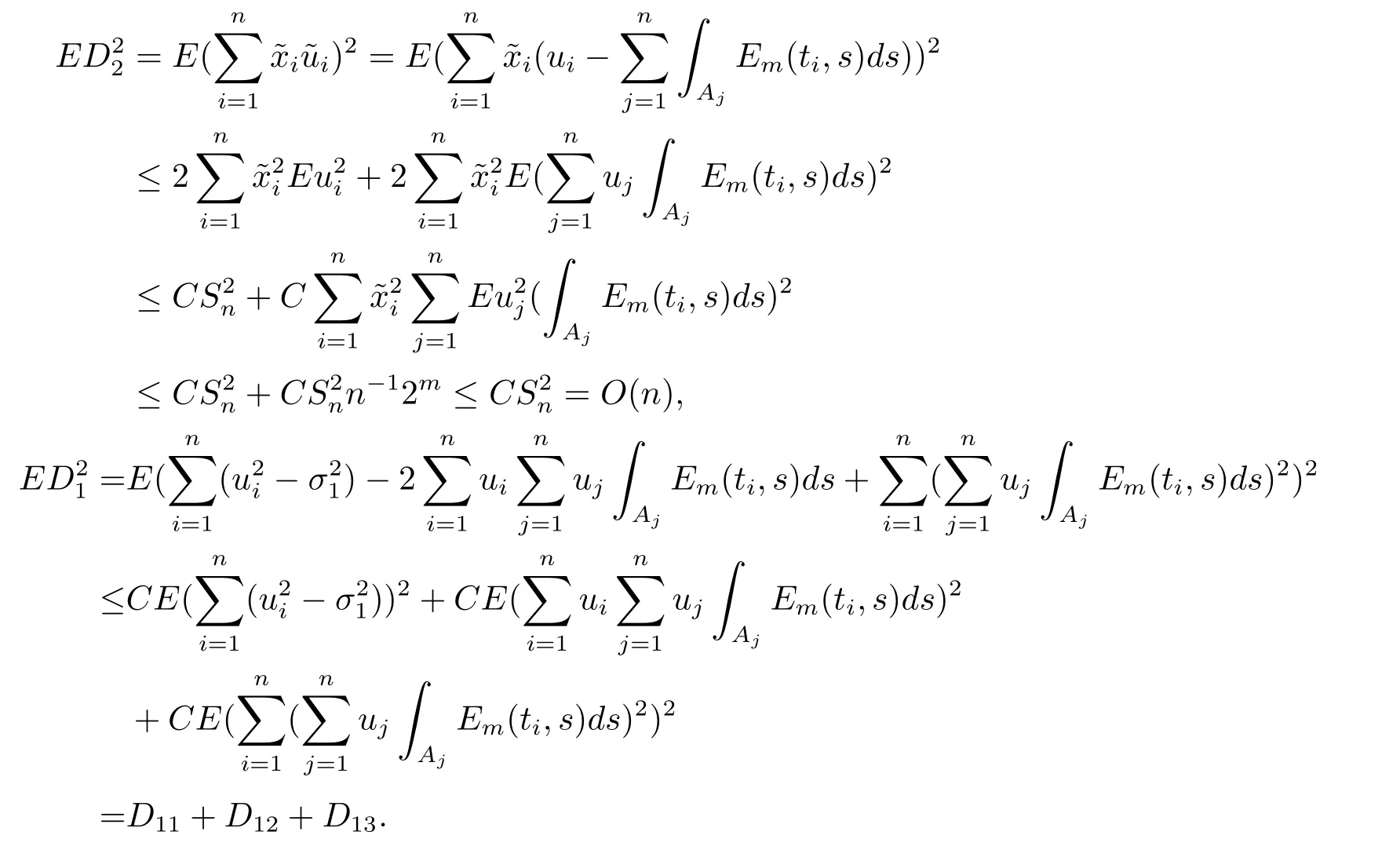




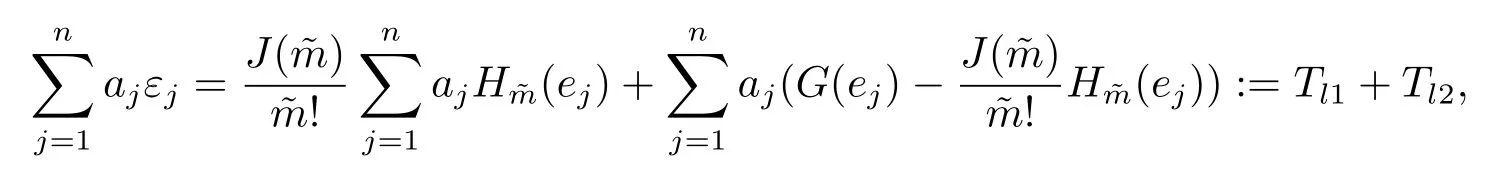
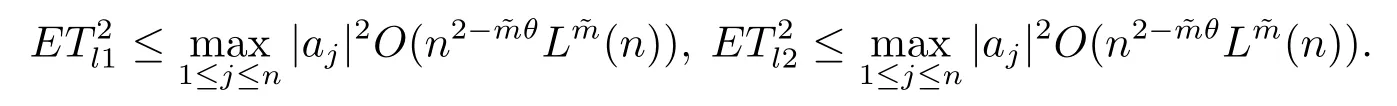


5 主要結果的證明




















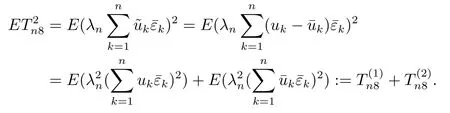

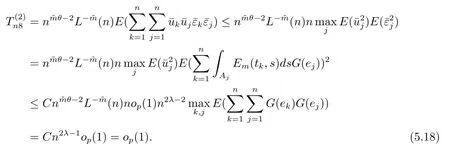






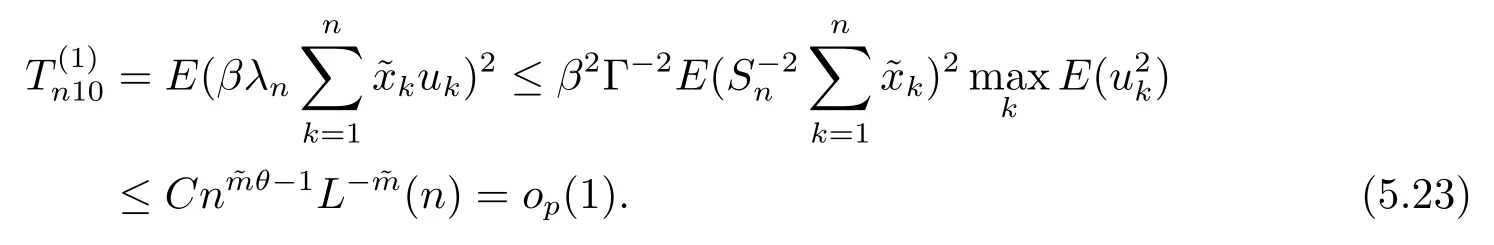
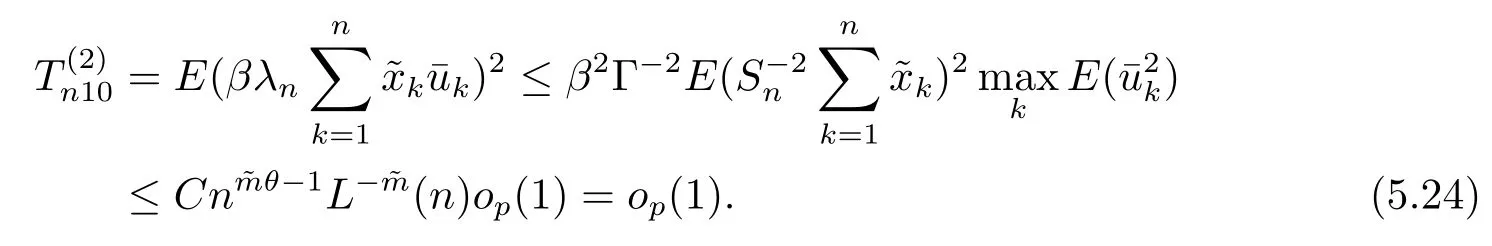






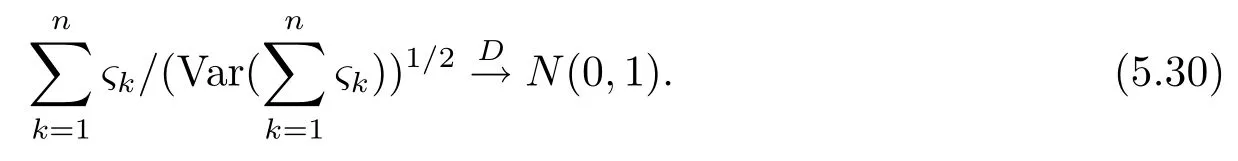








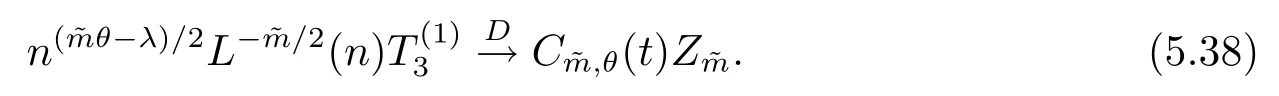


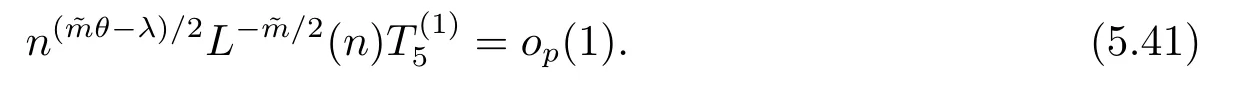
6 模擬例子