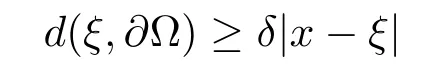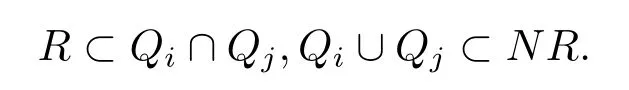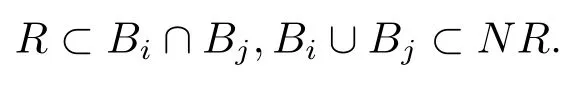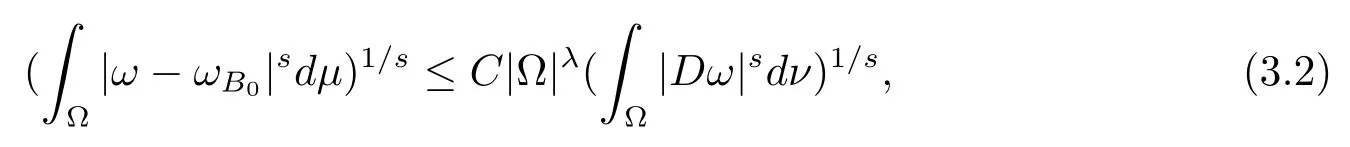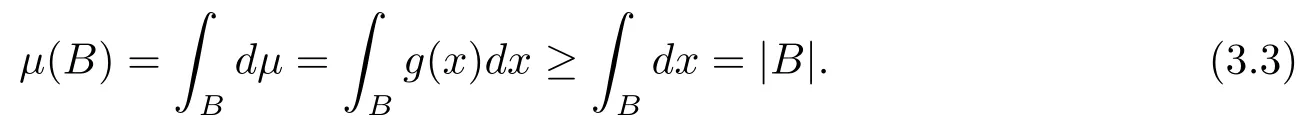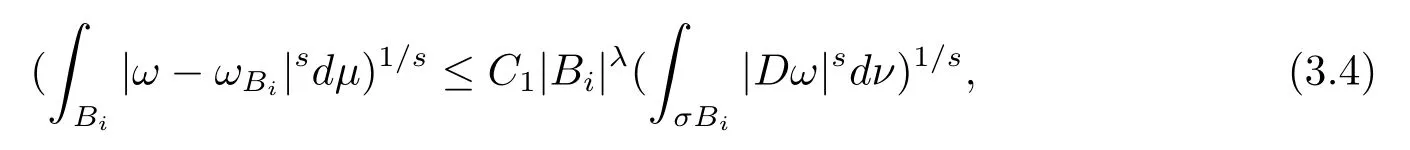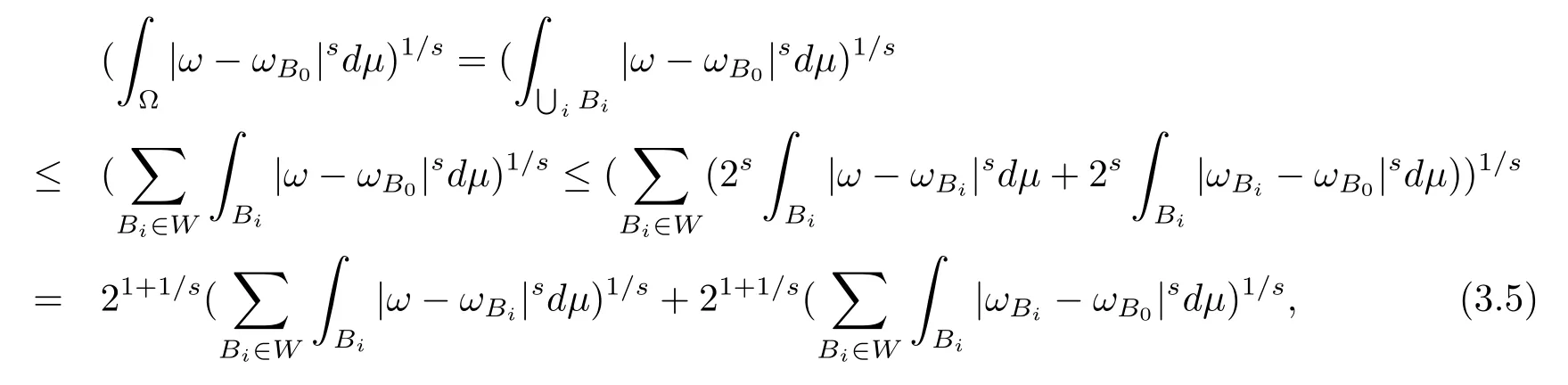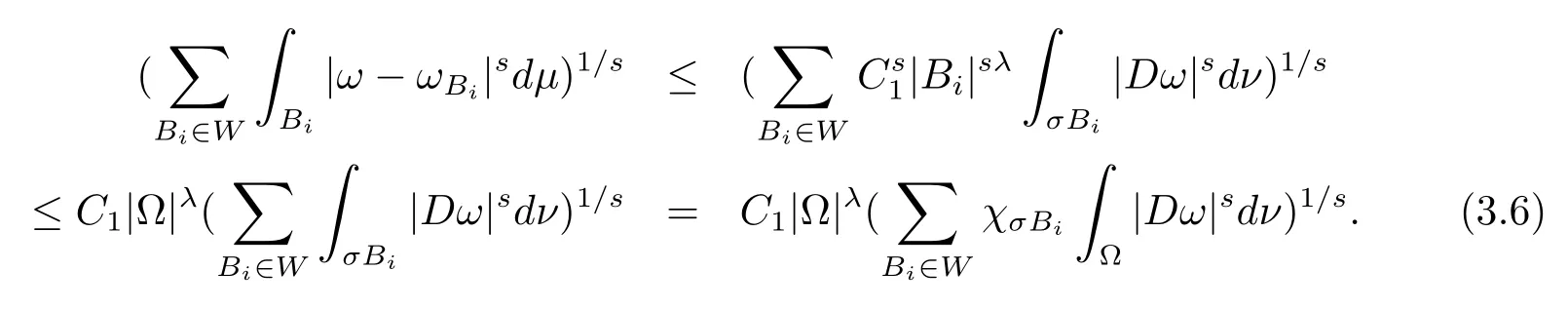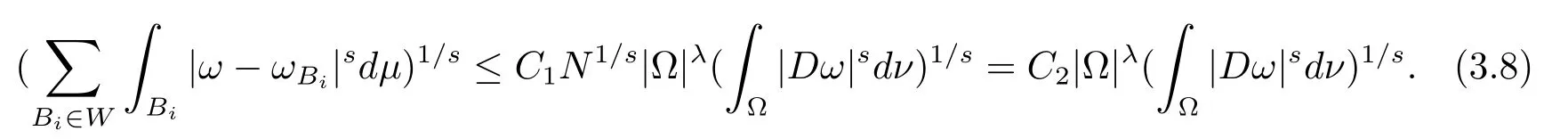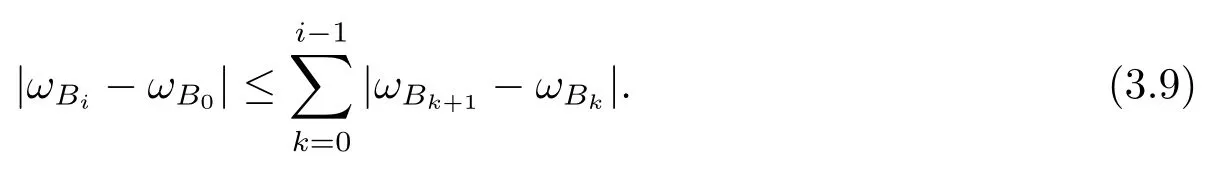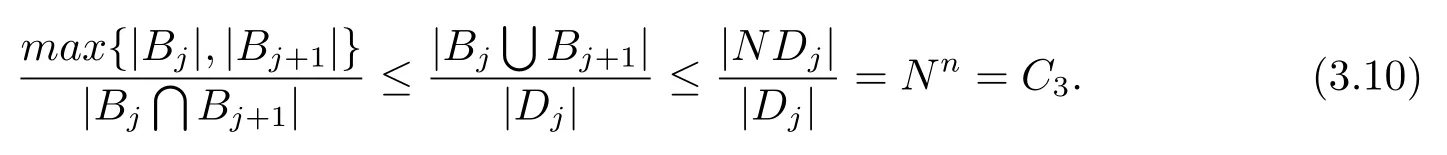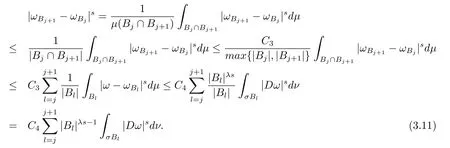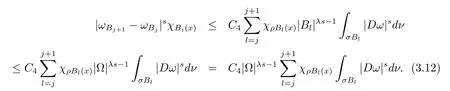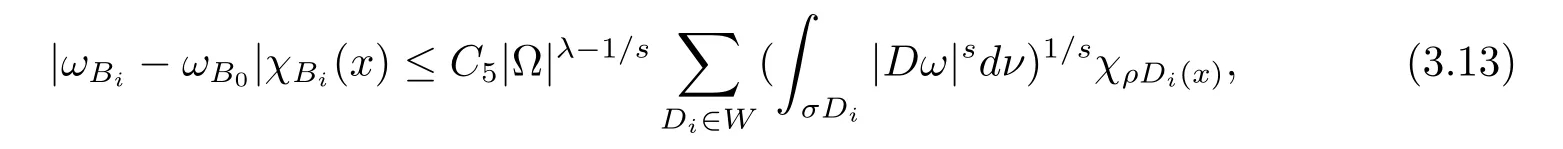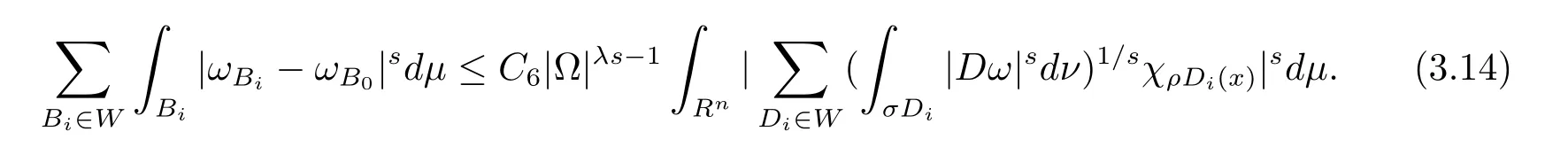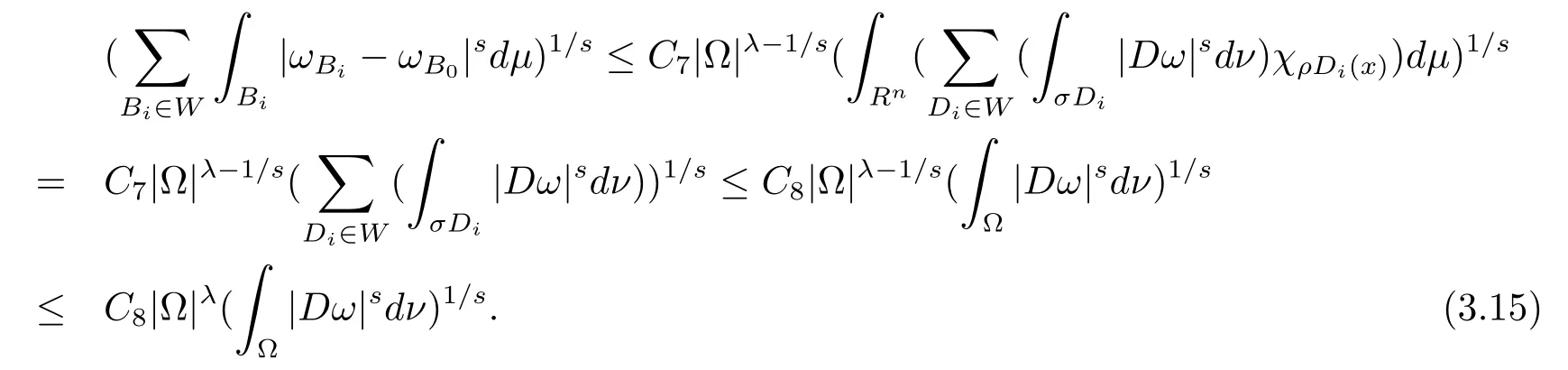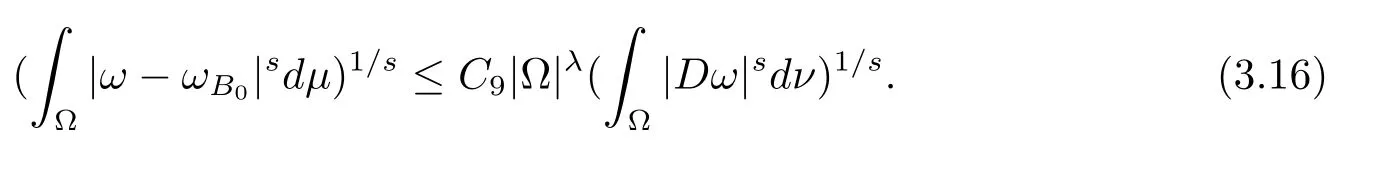關(guān)于Radon 測(cè)度的積分不等式
李華燦, 李群芳
(1.江西理工大學(xué)理學(xué)院, 江西贛州341000)
(2.贛州師范高等專科學(xué)校數(shù)學(xué)系, 江西贛州341000)
1 引言
近些年, 非線性彈性理論和擬共形映射的發(fā)展促使微分形式的橢圓方程的研究取得了極大的進(jìn)展, 已經(jīng)從最初的Laplace 方程擴(kuò)展到了A-調(diào)和方程.目前, 關(guān)于滿足A-調(diào)和方程的微分形式的研究已取得較豐富的成果, 如Ding, Weisz, Liu 等數(shù)學(xué)工作者們分別做出了作用于滿足A-調(diào)和方程的微分形式的Hardy-Littlewood-型、Poincar-型以及Caccioppoli-型經(jīng)典積分不等式[1?5], 文獻(xiàn)[6–9]進(jìn)一步地做出了上述三類經(jīng)典不等式的各類加權(quán)估計(jì)式.來源于理論物理學(xué)的Hodge-Dirac 算子, 不僅在量子力學(xué)和廣義相對(duì)論中有著極為重要的作用, 還為代數(shù)學(xué)和幾何學(xué)等數(shù)學(xué)分支領(lǐng)域的研究提供有力工具.2015 年, Ding 和Liu 在文獻(xiàn)[10]中借助于傳統(tǒng)的齊次A-調(diào)和方程d?A(x,dw)=0 和Hodge-Dirac 算子得到如下形式的齊次Dirac-調(diào)和方程

其中D稱為Hodge-Dirac 微分算子, 定義D=d+d?,d是外微分算子,d?是Hodge 上的微分算子定義為d?=(?1)nl+1?d?,?是Hodge 星算子,A是滿足特定條件的算子, 更多有關(guān)Hodge 星算子?、Hodge 上的微分算子d?以及算子A的詳細(xì)介紹可參見文獻(xiàn)[11].作為A-調(diào)和方程的衍生方程, Dirac-調(diào)和方程的理論研究目前仍處于起步階段, 其數(shù)學(xué)意義和實(shí)際作用還需要更深入的研究.因此, 本文將以滿足Dirac-調(diào)和方程的微分形式為研究對(duì)象, 首先研究作用于其上的關(guān)于Radon 測(cè)度的局部圓域上的Poincar-型不等式, 然后以此為基礎(chǔ)證明δ-John 域上全局的Poincar-型不等式.
本文通篇假定? 為Rn中的連通開子集,B為球體,ρB表示與B同心且diam(ρB)=ρdiam(B)的球體, 用|E| 來表示Rn中子集E的勒貝格測(cè)度, 文中所有積分均為勒貝格積分.設(shè)g(x)是定義在Rn上非負(fù)可積函數(shù), Radon 測(cè)度μ由dμ=g(x)dx給出, 即μ(E)=Eg(x)dx為Rn中子集E的Radon 測(cè)度.設(shè)e1=(1,0,··· ,0),e2=(0,1,··· ,0),··· ,en=(0,0,··· ,1)為Rn上標(biāo)準(zhǔn)正交單位向量組, 用Λl=Λl(Rn) 表示由外積eI=ei1∧ei2∧···∧eil所生成的l-維向量空間, 其下標(biāo)所對(duì)應(yīng)的有序l-叢I=(i1,i2,··· ,il), 1≤i1 本節(jié)將在有界域上證明作用于滿足Dirac-調(diào)和方程(1.1) 的微分形式的帶Radon 測(cè)度的局部Poincar-型不等式, 在本節(jié)的相關(guān)證明中將用到以下重要引理. 引理2.1[10]設(shè)ω是? 上Dirac-調(diào)和方程(1.1) 的解,p> 1 是與方程(1.1) 有關(guān)的確定指數(shù), 則對(duì)任意滿足σB?? 的球體B, 存在不依賴于ω的常數(shù)C, 使得 成立, 其中σ>1, 0 引理2.2[10]設(shè)u∈,Λl) 是微分形式則對(duì)滿足Q?Rn的球體Q, 有u?uQ∈Lp(Q,Λ) 且 其中C是不依賴于u與Du的常數(shù),p>1. 引理2.3(廣義Hlder 不等式) 設(shè)f,g是兩個(gè)定義在Rn上的可測(cè)函數(shù), 則對(duì)Rn中的任意子集E, 有 其中0<α<∞, 0<β<∞, 且s?1=α?1+β?1. 定理2.4設(shè)是有界域? 上滿足Dirac-調(diào)和方程(1.1) 的微分形式,則對(duì)任一滿足σB?? 的球體B, 存在不依賴于ω的常數(shù)C, 使得 上述Radon 測(cè)度μ,ν分別由dμ=g(x)dx,dν=h(x)dx定義,且其中K1> 0,K2> 0,n>α>β,σ> 1,均為常數(shù),xB為球體B的球心. 證設(shè)rB是球體B的半徑, 選取正數(shù)ε滿足0<ε 不妨設(shè)球體B的球心xB為原點(diǎn)O(若不然, 只需將xB平移至原點(diǎn)O即可), 利用多重積分的極坐標(biāo)變換可得 其中σ>1 為常數(shù).綜合Hlder 不等式,以及極坐標(biāo)變換, 得 從而有 式(2.9) 說明式(2.1) 成立, 故定理2.4 證畢. 本節(jié)將以定理2.4 中的局部圓域上的關(guān)于Radon 測(cè)度的Poincar-型不等式(2.1) 為基礎(chǔ), 結(jié)合δ-John 域的相關(guān)性質(zhì), 進(jìn)一步證明δ-John 域上關(guān)于Radon 測(cè)度的全局的Poincar-型不等式.在本節(jié)定理的證明中將利用下述關(guān)于δ-John 域的定義和性質(zhì). 定義3.1[12]設(shè)? 是Rn的一個(gè)子區(qū)域, 若存在一點(diǎn)x0∈?, 它與? 中任一點(diǎn)x均可以由? 中連續(xù)曲線γ連接, 且對(duì)任意ξ∈γ, 有 成立, 則稱? 為δ-John 域, 其中δ>0,d(ξ,??) 是ξ與?? 間的歐幾里得距離. 引理3.2[12](覆蓋引理)Rn中的每一連通開子集? 均有一個(gè)修正的立方體鏈的Whitney 覆蓋W={Qi}, 且存在某常數(shù)N>1, 對(duì)所有的x∈Rn, 有 成立, 其中χ是特征函數(shù).此外, 若則存在立方體R?Rn(R不必是W中的元素) 有下式成立 進(jìn)一步, 若? 是δ-John 域, 則對(duì)于W中每一個(gè)立方體Q, 存在一中心立方體Q0∈W, 它可以通過W中立方體鏈Q(jìng)0,Q1,Q2,··· ,Qk=Q將立方體Q連接起來, 并且有Q?ρQi成立,其中i=0,1,2,··· ,k?1,ρ=ρ(n,δ) 為一常數(shù). 因?yàn)榱⒎襟w與球體具有相互包含關(guān)系, 故可將引理3.2 中的立方體鏈{Qi} 替換為球體鏈{Bi}, 于是便可得到引理3.2 中關(guān)于δ-John 域的性質(zhì)如下等價(jià)描述. 引理3.2設(shè)Rn中的連通開子集? 是δ-John 域,則存在? 的Whitney 覆蓋W={Bi},滿足下述兩個(gè)條件 (1) 存在一常數(shù)N>1, 使得對(duì)所有的x∈Rn, 成立其中χ是特征函數(shù); (2) 存在一中心球體B0∈W, 它可以通過W中球體鏈B0,B1,B2,··· ,Bk=B將W中任何一個(gè)球體B連接起來, 且有B?ρBi成立,i=0,1,2,··· ,k?1,ρ=ρ(n,δ) 為常數(shù),并存在立方體R(R不必是W中的元素) 有下式成立 定理3.3設(shè)? 是δ-John 域,是? 上滿足Dirac-調(diào)和方程(1.1) 的微分形式則存在不依賴于ω的常數(shù)C, 使得 其中Radon 測(cè)度μ,ν分別由dμ=g(x)dx,dν=h(x)dx定義且這里K1>0,K2>0,β<α 證對(duì)? 中任意球體B, 由g(x)≥1 可得 其中σ>1 為常數(shù).應(yīng)用初等不等式可得 其中B0?? 是滿足引理中的一中心球體.由式(3.4) 可得 綜合式(3.6)–(3.7), 可得 綜合式(3.3),(3.10),(3.4), 便有 由β<α 其中x∈Rn.(3.13) 式兩端先作s次冪, 然后在Rn上作μ-積分, 可得 綜合式(3.5), (3.8), (3.15), 可得 定理3.3 證畢.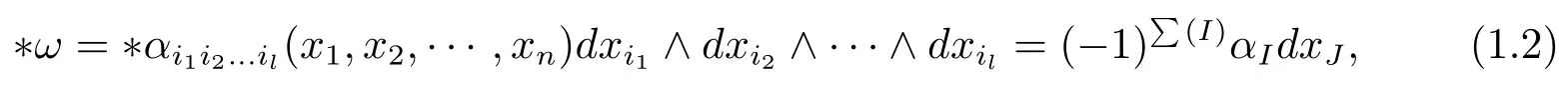
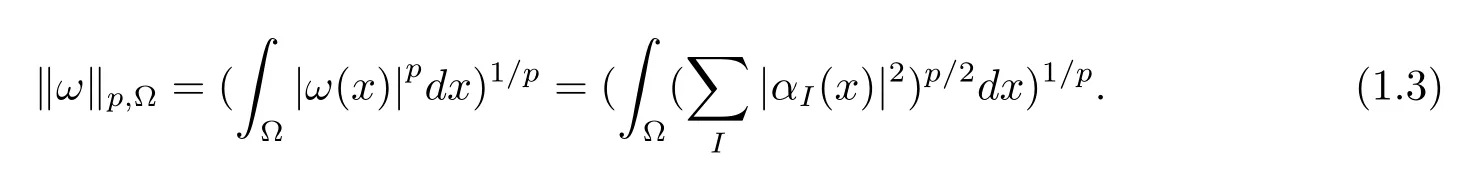
2 有界域上關(guān)于Radon 測(cè)度的局部Poincar-型不等式
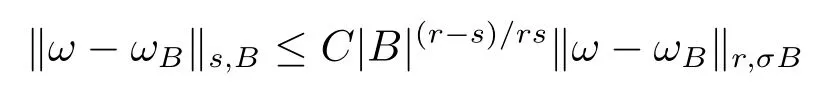
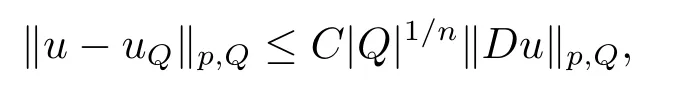
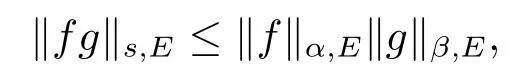
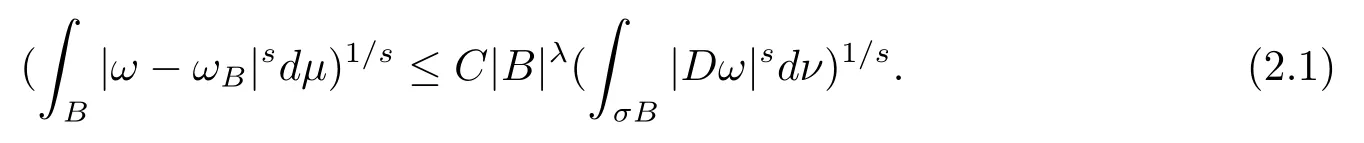
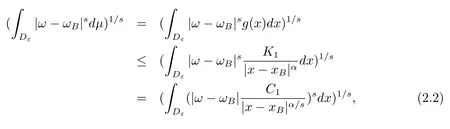
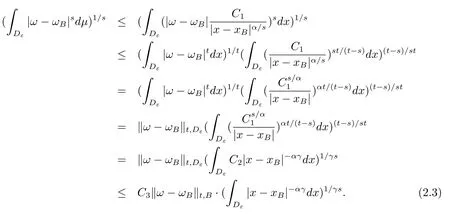
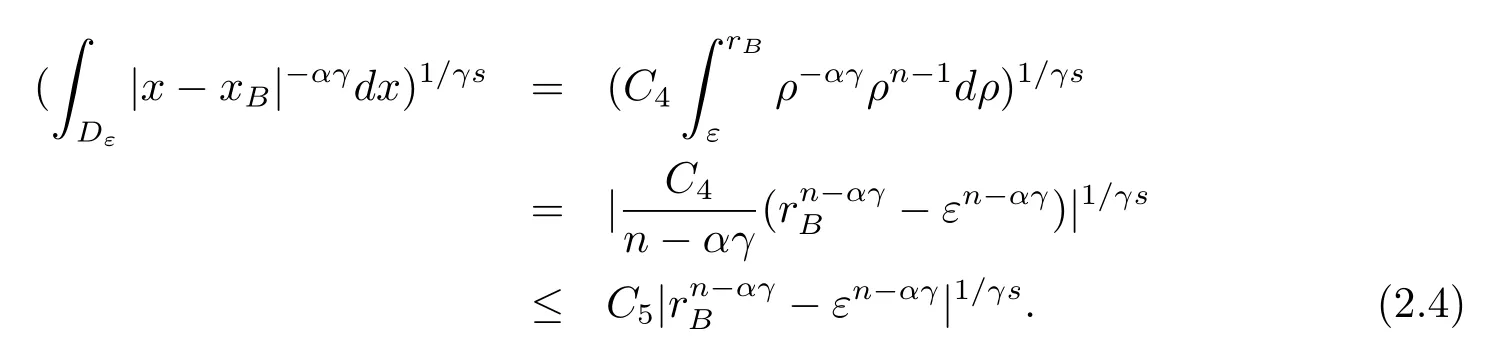
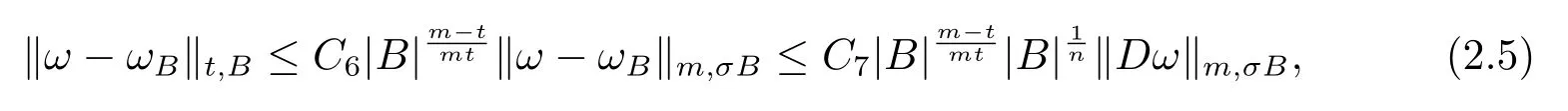
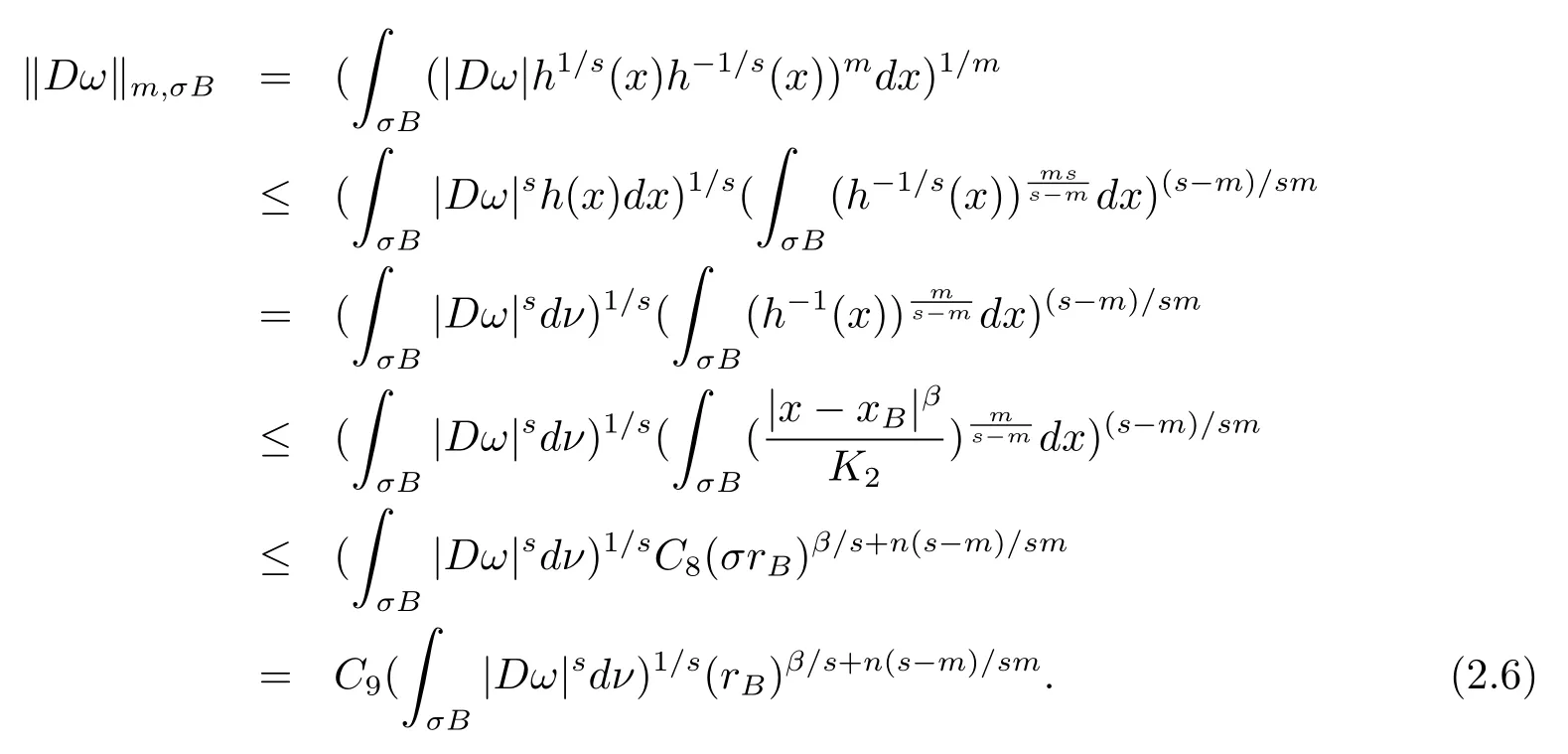
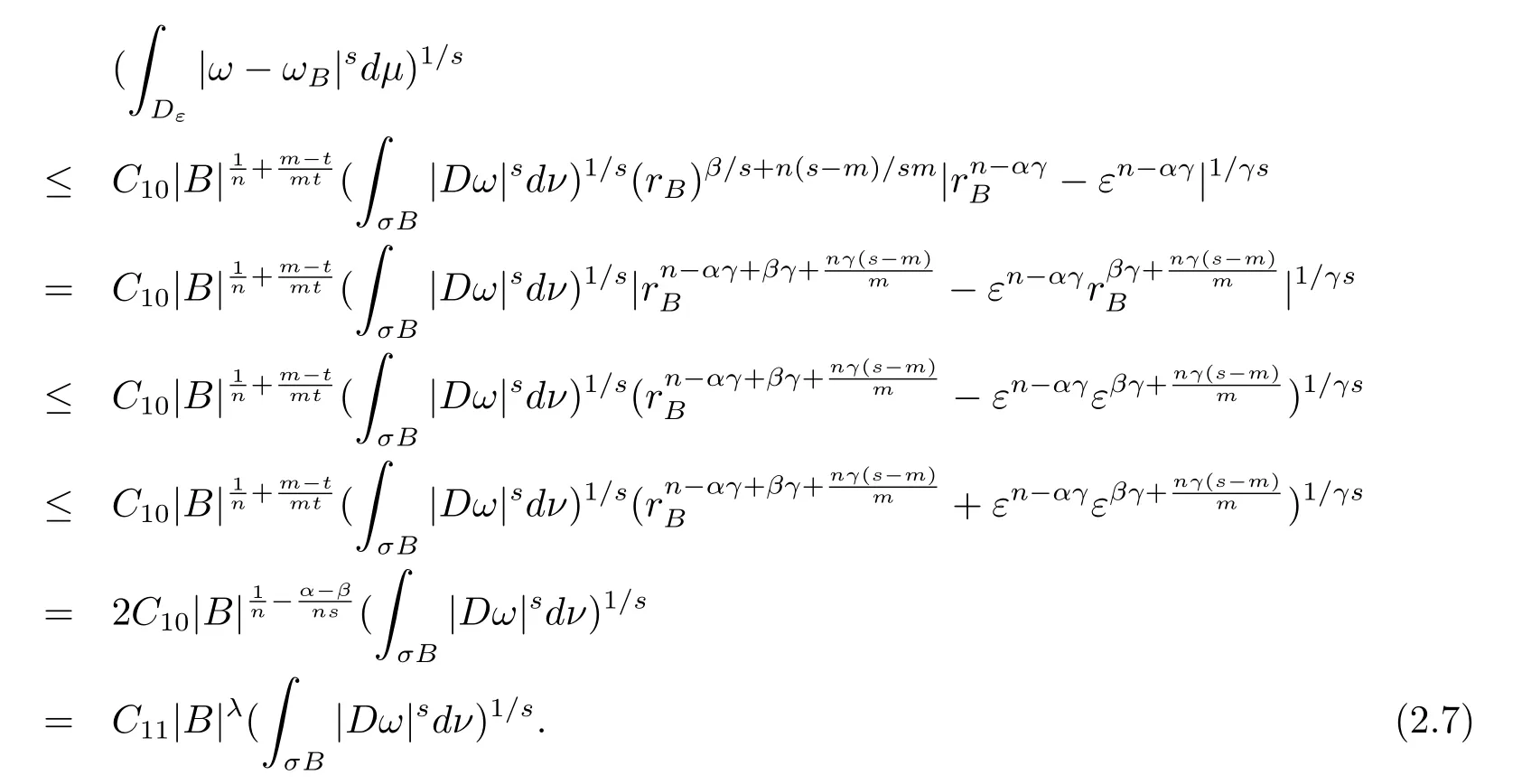
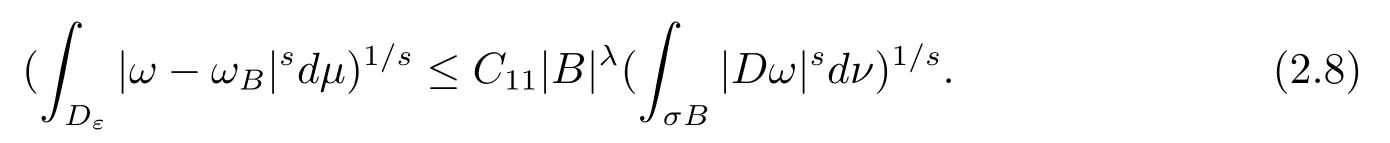
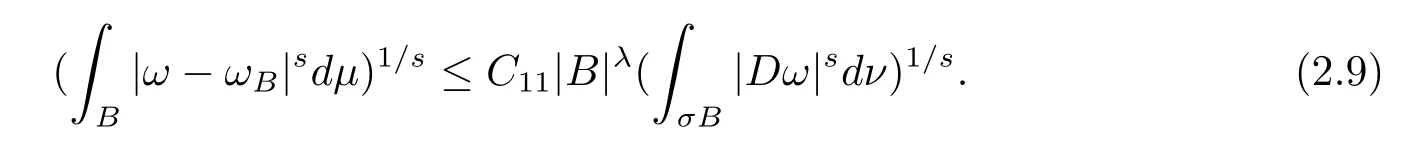
3 δ-John 域上關(guān)于Radon 測(cè)度的全局的Poincar-型不等式