數形結合方法在教學中的合理運用

陳伴榮

[摘 要]所謂數形結合，其實就是借助圖形、符號和文字等形式，協調形象思維和抽象思維的發展，從而達到溝通數學知識間的聯系，理解數學知識本質特征的目的。數形結合是小學階段解決數學問題常用的方法。數形結合對學生的數學學習起著重要的作用，“數缺形時少直觀，形缺數時難入微。”可見將數形結合思想貫穿數學教學的始終，是促使學生學好數學的關鍵。

[關鍵詞]數形結合;抽象;直觀

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2019）29-0096-01

小學生的思維能力、空間想象能力都比較弱，對于一些抽象的概念和問題，理解和解決起來比較困難。面對這種情況，我覺得教師應當采用數形結合的方式，將抽象的概念和問題具體化、直觀化，引導學生借助直觀圖思考，積極地解決數學問題，以此提高他們的邏輯思維能力，培養他們對數學的興趣。

一、用數形結合理解算理，讓學生知其然并知其所以然

計算是小學數學最重要的組成部分，小學階段是打好計算基礎的關鍵時期。然而對于小學生而言，算理是抽象的、難理解的，并且目前很多教師都是偏重于講解計算方法，忽視了算理，致使學生只會計算，不明算理，這禁錮了學生思維的發展。作為教師，應有意識地利用數形結合來設計教學，用看得見、摸得著的實物直觀形象地演示算理，降低學生的理解難度，使抽象概念具體化，讓學生對計算“知其然并知其所以然”。

例如，在教學“兩位數加兩位數進位加法”時，教師可以這樣設計教學：18+16，讓學生把小棒擺成豎式的樣子，就是一捆（10根）和8根，對應下面擺一捆（10根）和6根，從個位算起，個位上的8根加6根小棒就可以從中取10根捆成一捆，表示一個十，放到十位上去，這時十位上有三捆，就是3個10，個位還有4根。這樣可以讓學生輕松理解“滿十進一”的算理。

二、用數形結合掌握概念，揭示概念本質

概念教學是形成數學知識體系的基礎，也是“四基”教學的核心內容。小學數學中有很多概念，大多數學生常常對一些概念難以理解和掌握，不得已的情況下只能死記硬背，這樣不但達不到學習目的，反而漸漸對數學失去興趣，甚至產生抵觸、討厭數學的情緒。如果教師能充分挖掘、利用圖形的特質，讓“形”成為概念理解的“催化劑”，用“形”去闡述概念的本質，溝通數學知識之間的內在聯系，就可以使學生真正理解、輕松掌握概念的內涵。

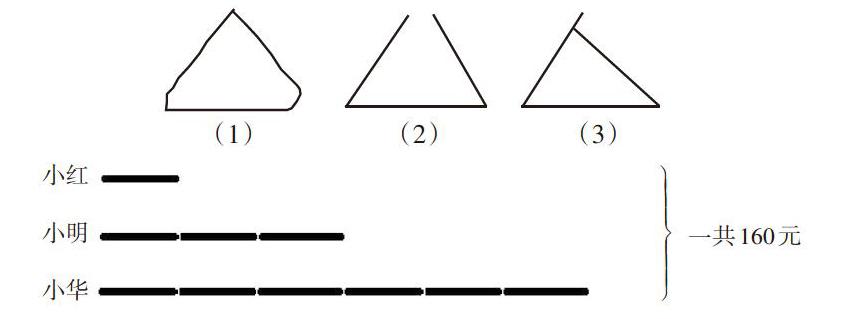
例如，在教學“三角形的認識”時，可以這樣引導學生理解三角形的概念：“你在哪里見過三角形？ 你會畫三角形嗎？ 請在紙上畫一個大小適中的三角形。”教師可以選擇三幅典型的圖來展示，如圖（1）的邊不是直線，圖（2）不是封閉圖形，圖（3）的邊沒有首尾相連。因此它們都不是三角形。

通過對比、討論，學生明確了由三條線段圍成（首尾相連）的封閉圖形叫三角形。這樣利用數形結合，學生很容易就理解和掌握三角形的概念。

三、用數形結合解決問題，讓復雜的問題簡單化

學生在面對一些比較復雜的數學問題時，很難只通過閱讀文字來理解數量之間的關系。這時教師就需要運用數形結合，將復雜抽象的數學語言轉化為簡單形象的圖形語言。實際上，一個簡單的圖像也能表達出復雜的數學內容，圖像語言是非常有利于數學思維表達的。我發現在教學中，當學生遇到難題，百思不得其解的時候，教師往往只要稍加指點或者畫個草圖，學生就思路大開，順利解決問題。

例如，有一道題：小明、小紅、小華合買了一套價格為160元的《格林童話》，小明出的錢是小紅的3倍，小華出的錢是小明2倍，他們各出了多少錢？遇到這類問題，很多學生很難把數量之間的關系搞清楚，所以在解決這類問題時，教師應當引導學生畫線段圖（如下圖），再解題。

從圖中很容易看出160元相當于小紅所出錢的10倍，各數量關系很清晰了，問題自然迎刃而解。

我國數學家張廣厚曾經說過：“抽象思維如果脫離直觀，一般是很有限度的。同樣，在抽象中如果看不出直觀，說明還沒有把握住問題的實質。”可見抽象思維與直觀思維有著密切聯系。在小學數學教學過程中，數形結合教學方法可以使學生學得輕松而有效。教師要善于根據學生的實際情況，靈活把握時機滲透數形結合思想，激發學生的興趣，更好地開展課堂教學，提高課堂教學效率，培養學生的數學素養。

（責編 黃 露）