基于新的無標度區確定方法求取分形路面不平度的分形維數*

黃 華徐 凱何培松

(1.南京斯諾森汽車設計有限公司上海分公司,上海200120;2.廣西機電職業技術學院,廣西 南寧530007;3.廣西玉柴機器股份有限公司,廣西 玉林537005)

1 W-M函數生成分形路面不平度

1.1 W-M函數

W-M函數最早是由德國數學家維爾斯特拉斯發現的,后經M.Majumdar和B.Bhushan修正得到了M-B模型,用來表征工程表面的具有分形特征的輪廓,此模型也常常稱作W-M函數.其形式如下：

式中,Z(x)為隨機表面輪廓高度;x為輪廓的位置坐標;G為幅度特征尺度;D為分形維數;Nl、Mu為整數;γn空間頻率,考慮到表面平整度和頻率分布,γ通常取1.5,n∈[Nl,Mu].最小空間頻率由采樣長度決定,若采樣長度為L,則最小空間頻率γNl=1/L;最大空間頻率γMu由采樣頻率F s確定,[1]γMu=Fs/2,采樣頻率Fs的取值需滿足采樣定理.

式(1)的連續功率譜密度表達式為：[2]

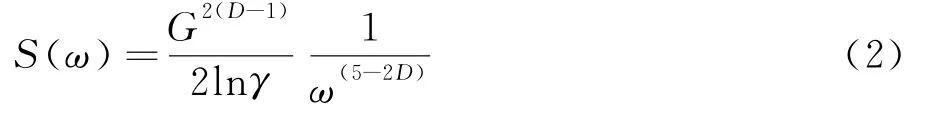
式中,ω是空間頻率.

1.2 路面不平度

路面不平度作為車輛系統輸入的主要激勵源,對車輛的振動、結構的疲勞特性影響較大,一直是人們研究的重點對象.經研究發現,隨機路面不平度作為一種不規則的、自相似性的幾何集,具有明顯的分形特征.[3]

根據1984年國際標準化組織在文件ISO/TC 108/SC2N67提出的“路面不平度表示方法草案”和國內標準GB 7031《車輛振動輸入—路面平度表示》,路面的統計特性用功率譜密度表示,兩文件建議其表達式為冪函數形式.形式如下：[4]

式中,n為空間頻率(m-1),它是波長的倒數,表示每米長度中包括幾個波長;n0為參考空間頻率,n0=0.1 m-1;G q(n0)為參考空間頻率n0下的路面功率譜密度值,稱為路面不平度系數,單位是m3;w為頻率指數,為雙對數坐標上斜線的斜率,它決定路面功率譜密度的頻率結構.另外,文件按照功率譜密度的不同將路面不平度分為8個等級,頻率指數w=2.

1.3 W-M函數生成分形路面不平度

基于分形維數的求解方法中的功率譜密度法,[5]通過式(2)和式(3)可用W-M函數生成分形路面不平度.A級和C級分形路面不平度如圖1和圖2所示.參數設置如表1所示.

圖1 A級分形路面不平度Fig.1 Roughness of Grade A fractal road

圖2 C級分形路面不平度Fig.2 Roughness of Grade C fractal road

表1 分形路面不平度仿真參數Tab.1 Simulation parameters of fractal road roughness

求取分形路面不平度的功率譜密度與標準功率譜對比,結果如圖3和圖4所示.由圖3和圖4可知,基于W-M函數生成的分形路面不平度反映了標準路面的統計特性,有較高的精度.

圖3 A級分形路面不平度的功率譜密度與標準譜的對比Fig.3 Comparison of power spectral density of Grade A fractal road roughness with standard spectrum

圖4 C級分形路面不平度的功率譜密度與標準譜的對比Fig.4 Comparison of power spectral density of Grade C fractal road roughness with standard spectrum

2 結構函數法求分形路面不平度的分形維數

2.1 結構函數法

結構函數法常用于粗糙面分形特性的分析和分形特征參數的求取,其定義為：[6]

離散化之后,進一步為：[7]

式(5)和式(6)中,S(τ)為結構函數;(τ)=n△l,n=1,2,3,…,N-1;△l為采樣距離間隔;〈·〉為差方的算數平均值;Z i為表面輪廓曲線的離散點,i=0,1,2,3,…,N;將S(τ)和τ用對數坐標表示,進行線性回歸,得到直線方程,設其斜率為K,則表面輪廓曲線的分形維數為

基于上述分形路面不平度,采用結構函數法求取分形路面不平度模型的分形維數,在將分形路面不平度的標度律,進行線性回歸分析,擬合直線方程之前,需首先確定無標度區.本文提出了一種新的無標度區確定方法.

2.2 無標度區確定的新方法

2.2.1 無標度區的定義

測度與標度在雙對數坐標呈現直線的區域稱為具有分形特征的尺度區域,也稱作無標度區.[8]無標度區越大,說明曲線具有較多層次的自相似結構,而在在無標度區之外應用分形理論是沒有任何意義的,同時,無標度區也是判別輪廓是否具有分形特征的重要參數.

2.2.2 確定無標度區的方法

目前確定無標度區的方法很多,有人工判定法、相關系數法、強化系數法、擬合誤差法、分維值誤差法和自相似比法等.[9]本文提出了一種新的無標度區確定方法,暫且稱之為“育苗法”.

2.2.3 新方法的原理和實現過程

根據分形理論,具有分形特征的理想曲線,存在無限小細分的自相似結構,在無標度區上表現為無限大范圍內的線性關系.而在實際自然界中,不存在理想的分形曲線,工程粗糙面表現為一段范圍內的無標度特征,因此,此區域內的標度與測度呈現良好的線性度.基于此,將雙對數坐標下的測度和標度構成的數據點排列在一維數軸上,以一定的規則選擇一部分數據點,然后以這些數據點向兩端擴展,計算這些數據點的相關系數和方差,在滿足一定的閾值下,包含較多數據點的區域,應為無標度區.

基于上述理論和思想,其實現過程是這樣的,將雙對數坐標內的數據點(τ,S(τ))看作排列在一維數軸上的點的集合.以等同的2個數據點為間隔,選擇一系列點,然后將這些選中的數據點作為“種子”標記在數軸上.以各個“種子”為中心,向數軸兩端外擴,每次外擴數量為2個數據點,計算各個“種子”區域內的相關系數,在滿足相關系數閾值下,再次外擴2個數據點,直至出現相關系數不滿足閾值.循環次數最多的“種子”包含的標度個數越多,自然標度區越大.在實際循環計算過程中,數據點外擴到數據軸端點之后應停止此方向端的外擴,只進行另一方向端的外擴.其實現過程可以描述為以下4個過程：

1)播種過程.

此過程實際上是將數據點進行分段處理,每段內有個標記的數據點,此點稱作“種子”,此過程也稱作“播種過程”,其標記結果如圖5所示.

圖5 數據點的標記過程Fig.5 Marking process of data points

2)“種子”自由生長過程.

此過程描述了各數據段不斷進行循環計算相關系數的過程,其中不滿足相關系數閾值的數據段不再參與下次循環計算,此過程以種子為中心,數據段不斷外擴,似種子的自由生長,滿足條件的不斷生長,不滿足生長條件的“死亡”.其生長過程如圖6所示,圖中實弧線表示第一次數據點外擴,虛弧線表示第二次數據點外擴,計算各數據段的相關系數的過程.

圖6 各數據段循環計算的過程Fig.6 The process of cyclic calculation of each data segment

3)培植過程.

培植過程主要是處理數據段外擴出現到達數軸端點問題.在“種子”生長到數軸端點時,此端點方向應停止生長,而另一側保持外擴相同的個數的數據點進行生長,直到不滿足相關系數閾值,其流程如圖7所示.

4)選苗過程.

選苗過程是“育苗”方法的核心步驟,主要是用來判斷各個“種子”的生長的區域能否成為無標度區的過程.具體過程為：根據過程1)～3)的計算結果,按照各個“種子”停止生長時包含的數據點個數由小到大的順序進行排列,同時標記出包含多個數據點的 “種子”對應的相關系數、雙對數坐標中測度的方差以及標度的上、下限,從這些數據可確定出無標度區.

“育苗”方法的流程圖,如圖8所示.

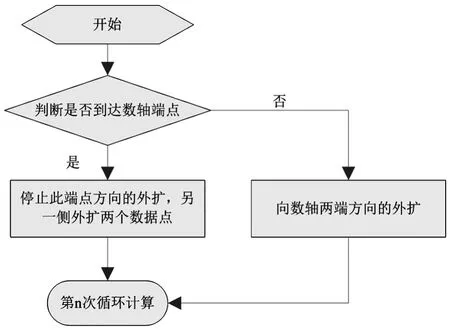
圖7 數據外擴到數軸端點的處理過程Fig.7 The process of data expansion to the endpoint of the number axis

圖8 “育苗”方法流程圖Fig.8 Flowchart of"nurturing"method

2.2.4 仿真結果分析

根據結構函數法,采用“育苗”方法確定無標度區,A級和C級分形路面不平度的標度律以及擬合直線如圖9和圖10所示.

根據圖9和圖10的擬合直線的斜率,結合式(6)求取的分形維數如表2所示.

圖9 A級分形路面不平度的標度律和擬合直線Fig.9 The scaling law and fitting line of Grade A fractal road roughness

圖10 C級分形路面不平度的標度律和擬合直線Fig.10 The scaling law and fitting line of Grade C fractal road roughness

表2 “育苗”法確定的無標度區求取的分形維數Tab.2 The fractal dimension obtained from the scale-free region determined by the"nurturing"method

3 人工觀測方法

為了對比驗證“育苗”算法的準確性,采取人工觀測的方法確定無標度區,求取的分形維數如表3所示.通過對比表2和表3可知,“育苗”方法作為一種新的思想和方法在確定無標度區和求取分形維數上具有較高的準確性,且實現了計算機自動處理,提高了計算分形維數的效率.

表3 人工觀測的方法確定無標度區求取的分形維數Tab.3 The fractal dimension obtained from the scale-free region determined by the manual observation

4 結論

通過W-M函數的連續功率譜密度函數,結合標準路面譜,生成了分形路面不平度.采用結構函數法求取了分形路面不平度的標度律,該標度律說明分形路面不平度具有分形特征.本文提出了一種新方法確定了分形路面不平度的無標度區,求取了分形維數;同時,采用人工觀測法確定了無標度區,并求取了分形維數.通過對比可知,本文提出的方法求取的分形維數與理論分形維數較為接近,比人工觀測法精度高.

未來,可研究此方法在確定具有多重分形特征的曲線的無標度區和求取分形維數的準確性,另外可用洛倫茲方程進一步檢驗該方法的準確性.W-M函數曲線是無限項尺度為的隨機相位余弦函數組成,其與生成路面不平度的三角級數法之間有何聯系也是研究方向之一.

此外,作者研究發現W-M函數的相似形式：

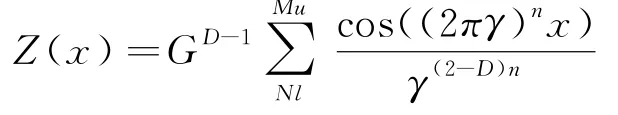
比式(1)在描述路面不平度上精度更高,且可用于車輛平順性仿真分析,后續研究可圍繞此展開.