分布圖和點圖分析在產品質量控制中的應用

王進峰， 花廣如， 潘麗娟， 劉彥豐

(華北電力大學 a.機械工程系; b動力工程系,河北 保定 071003)

0 引 言

在批量生產中，產品的質量控制通常采用統計學原理進行統計分析、控制，而統計分析產品質量最常用的兩種方法為點圖分析和分布圖分析[1]。點圖分析的優點是計算量小，能夠及時發現生產過程是否失穩，但是不能甄別常值系統性誤差;分布圖分析優點是能夠根據產品質量數據幀別出常值系統性誤差，但其計算量大，對工藝過程穩定性的判斷往往滯后于生產過程[2]。在工業生產中，批量生產隨處可見，利用統計學原理對產品質量進行控制是常規手段。顧亞鋒等[3]通過具體的工程案例,介紹了排列圖法在工程項目質量管理與控制中的應用。王曉峰[4]利用分層法、排列圖法、直方圖法得出的數理統計結果，提出具體的礦井瓦斯抽采工程質量問題分析結果。饒雄等[5]以發動機缸蓋關鍵工序加工誤差分析為研究對象,應用數理統計方法建立加工誤差統計分析模型,基于分布曲線法和點圖法設計模塊化分析系統。周飛[6]利用統計學方法分析飛機裝配過程中的質量數據，進行利用分析結果控制飛機的裝配質量。楊鋒等[7]利用統計分析手段控制鋼結構涂裝質量。劉必英[8]嘗試進行正交試驗，并利用統計方法對紡紗質量實驗數據進行分析。于靖華[9]對加工誤差的統計分析法進行了研究，論述了分布圖分析法和點圖分析法的理論。梁毅等[10]利用分布圖對藥品的產品質量進行分析控制。羅婭運[11]用點圖分析機械加工工藝過程穩定性。魯俊環[12]將點圖分析應用與備件庫存管理中。由于統計分析方法在批量生產質量控制方面的優勢，不僅高校進行基礎理論方面的研究[13-14]，而大型企業也在用較為成熟的商業軟件解決實際工程問題[15]。

為了說明分布圖分析法和點圖分析法在產品質量控制中的應用，便于開展教學實驗，本文設計了一種實驗方法，可同時對生產工藝系統進行分布圖分析和點圖分析，以便于對工藝系統進行評價。

1 實驗過程

2 點圖分析

根據測量的零件尺寸數據，確定4個零件為一組小樣本。計算各個小樣本的尺寸均值和極差,如表2所示。

表1 零件尺寸 mm

表2 小樣本均值與極差 mm

(1)

(2)

(3)

(4)

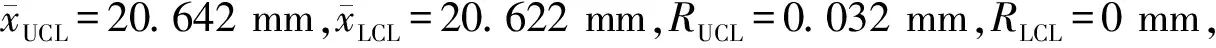
圖2 均值點圖

圖3 極差點圖

根據零件小樣本的均值和極差分布情況可判斷生產過程是否穩定。圖2和圖3表明：調整法加工100個棒料的生產過程是穩定的。點圖分析能夠及時判斷生產過程是否失穩，但是不能計算整個生產過程的工序能力，也不能甄別系統中的常值系統性誤差，因此，嘗試使用分布圖分析工藝過程的穩定性及工序能力。

3 分布圖分析

首先計算100個樣本零件的均值和標準差:

(5)

式中，xi為工件尺寸。

根據分布圖分析，100個樣本零件尺寸數據分為11組，尺寸間隔為0.003 mm，下限為20.615 mm，上限為20.648 mm，統計各尺寸間隔，樣本零件出現的頻數如表3所示。

將表3的數據表示直方圖如圖4所示，其中橫坐標為分組中值，縱坐標為零件出現頻數。為了甄別系統的常值系統性誤差，便于計算產品的合格品率、不合格品率，將直方圖擬合為正態分布圖，如圖5所示。

表3 尺寸分組和頻數

圖4 直方圖

圖5 直方圖與分布圖

從擬合的正態分布圖可以看出，零件尺寸基本符合正態分布，表明工藝過程是穩定的。為了衡量工藝過程的穩定性，進一步計算工序能力及合格品率和不合格品率。將正態分布函數轉化為標準正態分布函數

(6)

(7)

式中：x1是尺寸上限;x2是尺寸下限。

查表可得合格率為

0.5+φ(2.57)=0.5+0.494 5=99.45%

不合格率為

1-0.994 5=0.55%

工序能力等級

Cp=T/(6σ)=0.04/0.042=0.95

查工序能力表發現該工藝系統為3級工序能力，工序能力略有不足，應采取措施提高工序能力，加強質量檢驗，必要時全數檢驗或增加檢驗的次數。

4 結 語

為了滿足產品質量控制課程教學的需要，設計了一種集成分布圖分析和點圖分析的產品質量控制方法。首先通過順序采集25組由4個零件構成的小樣本進行均值和極差的計算，確定均值和極差的點圖分布，以確定工藝系統是否穩定。然后通過100個零件作為大樣本，進行均值和標準差的計算，確定直方圖，并擬合正態分布，以確定生產過程是否穩定。并利用擬合的正態分布圖來計算合格/不合格品率，工序能力等工藝系統參數。