庫水作用下滑坡體內侵蝕特性的數值模擬

王平凡， 畢金鋒， 羅先啟

(上海交通大學 船舶海洋與建筑工程學院，上海 200240)

0 引 言

堤壩結構或邊坡工程長期受到庫水位或降雨的影響，土體結構由于滲流影響會發生內部失穩，內侵蝕作用已經成為導致潰壩及滑坡的主要因素之一。如1998年，長江九江段4號閘與5號閘之間決堤，潰口發生前堤防下游坡后有較多滲透變形跡象，隨后發展為堤防潰口。

目前，在諸多研究土體內侵蝕的試驗中，主要研究的是影響內侵蝕的因素和細顆粒流失規律。Benamar等[1]在不同的流動條件和土體力學參數下進行滲流試驗，研究內侵蝕的發生機理和動力學特性；李喜安等[2]利用解析方法推導內侵蝕發生的臨界條件，指出內侵蝕發生的臨界條件應由具體受力情況來分析；Marot等[3]研究內侵蝕過程中土體密度、孔隙壓力和被侵蝕顆粒的質量變化，表明細顆粒流失導致孔隙壓力增加，進而出現局部失穩；Chang等[4]對內侵蝕試樣進行三軸壓縮試驗，測試土體力學特性受內侵蝕作用的影響程度，當細顆粒流失量達到一定量級后，土體由剪脹變為剪縮。Bonelli等[5]對管涌中細顆粒流失規律進行研究，建立流體、被侵蝕顆粒和土體整體的質量守恒方程；Sterpi[6]提出一種計算細顆粒流失速率的方法，通過可被侵蝕細顆粒的質量計算在任意時刻下被侵蝕的細顆粒的質量；吳夢喜等[7]對細顆粒流失量不同的土體進行三軸和側限壓縮試驗，將土體的應變增量分成由應力和模量衰化引起的應變增量。

另外，還有學者借助有限元模擬內侵蝕過程來分析內侵蝕特性。Sibille等[8]利用離散元和格子波爾茲曼法來模擬內侵蝕過程中細顆粒從骨架顆粒脫離并隨水流運移，通過流體作用在顆粒上的功來耦合兩者之間的相互作用；Zhang等[9]根據熱力學原理和多孔介質理論建立內侵蝕結構模型，解釋管涌現象在臨界水力梯度的區域加劇原因；Sterpi[6]結合被侵蝕顆粒的質量守恒方程和基于滲流實驗得到的侵蝕規律，建立起細顆粒侵蝕與運移的有限元模型；劉忠玉等[10]建立臨界水頭梯度與細顆粒流失的關系，采用有限元方法分析細顆粒流失對工程穩定性的影響。羅玉龍等[11]結合潛蝕本構方程和土體三相質量守恒方程，建立有限元數值模型研究管涌過程中的內侵蝕作用。

在上述文獻中，試驗所采用的樣本是重塑土，這與天然土存在較大的差異，試驗得到的內侵蝕開始和結束條件與真實情況有些許差別。而且有限元模擬采用的控制方程沒有將質量守恒方程、連續性方程、滲流控制方程耦合起來，只是單獨考慮一個方面或只是耦合了其中兩個控制方程。本文參考其他學者所做的細顆粒流失試驗和內侵蝕控制方程，以錦屏呷爬滑坡為例，采用有限元的方法，耦合質量守恒方程、連續性方程和滲流方程建立改進后的內侵蝕數值模型，研究內侵蝕發生時不同的水頭對土體的孔隙率、被侵蝕顆粒的質量、細顆粒流失速率的影響。

1 內侵蝕形成條件

水流流過土體內部而將細顆粒帶走的現象稱為內侵蝕。內侵蝕過程中，土體內部細顆粒在滲透力作用下發生松動并脫離主骨架，從而造成土體的局部孔隙率增大，隨著水對土體的內侵蝕作用的加劇，會在局部形成優勢路徑或孔洞，土體骨架遭到破壞，局部強度削弱，容易造成土體整體在優勢路徑所在平面上發生剪切破壞。

沙金煊[12]通過對作用在單個土顆粒上的滲透力的計算，提出滲透侵蝕臨界水力坡降的近似公式

(1)

式中：r為可被侵蝕顆粒粒徑;k為滲透系數;φ為孔隙率。

《水利水電工程地質勘察規范》中對于間斷級配的土體，以間斷區間的中間值作為可被侵蝕的細顆粒的粒徑。根據錦屏一級水電站壩址相關勘察報告及工程經驗，確定呷爬滑坡可被侵蝕的細顆粒最小粒徑為1 mm。滑坡體的滲透系數約為0.3 mm/s，孔隙率約為0.3，故發生內部侵蝕的臨界水力坡降約為0.398。

圖1為庫水位線處的水力梯度變化圖，從圖中可以看出，隨著庫水位的變化，水位線處的水力梯度大致在0.52～0.65范圍內變化，大于臨界水力坡降，所以在庫水位以下的滑坡體內會發生內侵蝕現象。為了模擬出滑坡體在內侵蝕過程中土體的孔隙率、被侵蝕顆粒的質量、細顆粒流失速率等，需要建立相應的內侵蝕控制方程。

圖1 水力梯度變化圖

2 內侵蝕控制方程

2.1 內侵蝕下的質量守恒方程

在內侵蝕過程中，細顆粒從土體骨架脫離出來并隨水運動。假設其運動速度與水的流速一致，Cividini等[13]利用質量守恒定律得到內侵蝕作用的連續性方程：

(2)

式中：ρtr為被侵蝕的細顆粒的密度；vi為被侵蝕顆粒在i方向上的移動速度；qe為單位體積細顆粒被侵蝕的速率；qdp為被侵蝕顆粒沉積到土骨架的速率。

Vardoulakis等[14]將飽和多孔介質單元體分為未被侵蝕的土體、水和被侵蝕的細顆粒三部分,質量分別為dMs，dMw，dMfs，體積分別為dVs，dVw，dVfs。當有細顆粒被侵蝕時，細顆粒隨水一起流動，被侵蝕的顆粒和水組成的流動體密度為

(3)

式中：ρs為土顆粒的密度；ρw為水的密度；c為被侵蝕細顆粒的體積分數。被侵蝕顆粒的密度為

(4)

將式(4)代入(2)，則內侵蝕作用的連續性控制方程可以改寫為

(5)

2.2 內侵蝕下的滲流方程

發生內侵蝕時，土體內滲流狀態十分復雜，達西流、非達西流、優勢流可同時存在，且描述土體滲流狀態的方程也不盡相同。但在內侵蝕發生的初期，土體中的滲流以達西流為主，故本文采用達西定律來表示內侵蝕下的滲流方程，即

Vw=k▽p

(6)

Kozeny-Carman公式是描述多孔介質的滲透率與孔隙率關系精度最高的經驗公式，其表達式為

(7)

式中：η為Kozeny常數，將初始滲透率k0和初始孔隙率φ0代入上式，可得

(8)

則式(5)可以寫為

(9)

隨著內侵蝕的發生，流速增大，雷諾數隨之增大，流體的滲流速度與水力梯度之間將不再呈線性關系，達西定律不再適用，可改用福希海默方程[15]等描述非達西流的滲流方程。

2.3 內侵蝕速率

Cividini等[16]根據對重塑土樣的室內試驗，認為在一定水力梯度下一直對土體進行內侵蝕作用，最終也不會將全部的細顆粒帶走，而是會有細顆粒殘留在土體內。在滲透作用下，土體內部的細顆粒被侵蝕，被侵蝕的顆粒粒徑由小變大。所以設土體的骨架可被侵蝕的最大顆粒為rmax，可被侵蝕的顆粒最小粒徑為rmin。如果rrmin時，則細顆粒有可能被侵蝕出來。所以，本文考慮在呷爬滑坡土體級配曲線上，只有顆粒粒徑在rmin和rmax之間的顆粒才考慮內侵蝕速率。

(10)

式中，土體的體積變化率為

(11)

(12)

式中：φ為侵蝕后土體孔隙率，

φ=dVfs/dVs+dVw

3 呷爬滑坡內侵蝕特性分析

3.1 基本情況

錦屏呷爬滑坡位于錦屏一級水電站壩址上游11.5 km，前緣高程1.655 km，與枯期河水位持平，后緣高程2.120 km，滑坡縱長約880 m，寬約260～300 m，滑體平均厚度約60 m，體積約1.3×107m3。滑體物質主要為塊碎石土，滑帶厚1～8 m，主要由灰黑色泥夾碎石組成[17]。

前期勘察表明：呷爬滑坡除水庫蓄水至正常蓄水位(1.880 km高程)或迭加VII度地震時，滑體有滑動的可能，其余工況均能保持穩定或基本穩定，根據滑體物質組成及現今地形特點分析，預計失穩方式將以逐級牽引式滑塌為主。

水庫蓄水期，呷爬滑坡前緣見小規模次級滑塌，整體未見明顯變形破壞跡象。2015年11月水庫第2次蓄水至1.880 km后調查，發現呷爬滑坡產生整體蠕滑，在高程約1.900、2.050 km及后緣地帶出現貫通性拉裂縫。直至2017年6月庫水位消落至1.800 km后調查，發現呷爬滑坡仍在整體滑移，坡體原有拉張裂縫的下錯幅度有明顯增加，其中，最后緣貫通裂縫最大下座高度已大于200 cm，較2016年1.800 km水位調查時增加約50～70 cm，表明呷爬滑坡的變形仍在增加。該呷爬滑坡的地形圖和地質剖面圖如圖2和圖3所示。

圖3 呷爬滑坡地質剖面圖

3.2 內侵蝕特性分析

本文利用COMSOL Multiphysics軟件建立有限元模型，求解滲流和侵蝕耦合控制方程組，即式(5)、(6)和(12)。

根據圖2的滑坡地形圖和圖3的地質剖面圖,忽略滑坡的中上部裂縫與后緣裂縫，建立數值分析的模型。在數值模型中，認為水為不可壓縮流體，固體顆粒的壓縮量極小可以忽略，并且不考慮流體中含有細顆粒時對黏滯系數的影響，根據實驗結果和級配曲線，各參數取值如下:ρw=1 000 kg/m3,Es=80 MPa,μw=1.0 mPa·s,νs=0.35,φbr=0.2,φs=0.348 3,Kbr=0.01 mm/s,ρs=2 100 kg/m3,k0=0.4 mm/s,rmin=1 mm/s,φ0=0.3,rmax=6 mm。

整個模擬試驗過程持續525 d，水頭邊界條件根據實測的變化情況施加在模型邊界上。滑坡體表面為透水邊界，滑帶為不透水邊界，初始水頭邊界條件根據實測水位取值；孔隙率的初始條件設置為φ0；試驗開始時的水頭與試樣的上邊界一致，初始速度場v為0；在考慮重力的情況下，模型內部的初始壓力為重力產生的壓力場，即p0=ρwgz。

根據數值模擬的結果可以得到滑坡體在庫水位作用下的滲透率k、被侵蝕顆粒的體積分數φ以及內侵蝕速率qe的變化情況。

圖4為1.80 km和1.84 km高程處在庫水位變化情況下，滑坡體內滲透率k的變化情況。1.80 km是測量周期內的最低水位，此處始終受到內侵蝕的作用。從圖中可以看出，在內侵蝕持續作用的整個過程中，不斷有細顆粒被侵蝕，滑坡體的滲透率一直在增大且逐漸趨于平穩。內侵蝕發生的初期0～200 d，滲透率的斜率較大，表明有大量粒徑大于rmin的可被侵蝕顆粒被水流沖刷帶走；中期200～450 d內，由于小粒徑的顆粒逐漸變少以及顆粒在滲流通道內的累積，滲透率的變化趨勢變緩；450 d以后，大部分可被侵蝕顆粒都被侵蝕掉了，但仍有少量粒徑接近rmax的顆粒被侵蝕，此時內侵蝕作用效果逐漸減弱，滲透率也趨于平穩，最終將保持不變。在1.84 km高程處的滲透率與1.80 km處的滲透率變化規律相似，但在75～165 d及405 d以后，庫水位在1.84 km以下，所以此時高程1.84 km處不受庫水位的作用，內侵蝕作用暫時停止，被侵蝕顆粒的量為0，在圖中表現為滲透率曲線保持水平狀態。當庫水位再次超過1.84 km時，內侵蝕又再次發生。由于越往下的部分受到庫水作用的時間就越長，受到內侵蝕的時間越來越長，滲透率越大，故1.80 km高程處的滲透率比1.84 km高程處的滲透率大。

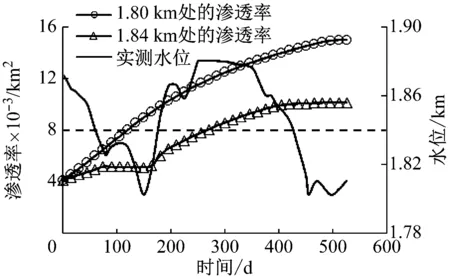
圖4 滑坡體內滲透率的變化

圖5為不同高程下滑坡體內可被侵蝕顆粒的侵蝕量占土體的體積分數φ，與滲透率的變化規律基本一致。1.80 km高程處完全處于水下，受到的內侵蝕時間最長，被侵蝕的細顆粒越多。可被侵蝕顆粒占土體的體積分數的定義與孔隙率的定義類似，對于顆粒粒徑小于rmax的顆粒可以看作在內侵蝕發生之前就已經被侵蝕掉了，此時的可被侵蝕顆粒的體積分數相當于土體的初始孔隙率0.3，對于粒徑處于rmin和rmax之間的顆粒，則需要在庫水的作用下被侵蝕掉。從圖中的趨勢線可以看出，如果在525 d之后庫水位超過1.84 km，那么1.84 km高程處的可被侵蝕顆粒的φ將沿著原來的增長趨勢繼續增加，最終將和1.80 km高程處的φ值趨于同一個穩定的φmax。當所有可被侵蝕的顆粒全部被侵蝕完之后，內侵蝕結束。

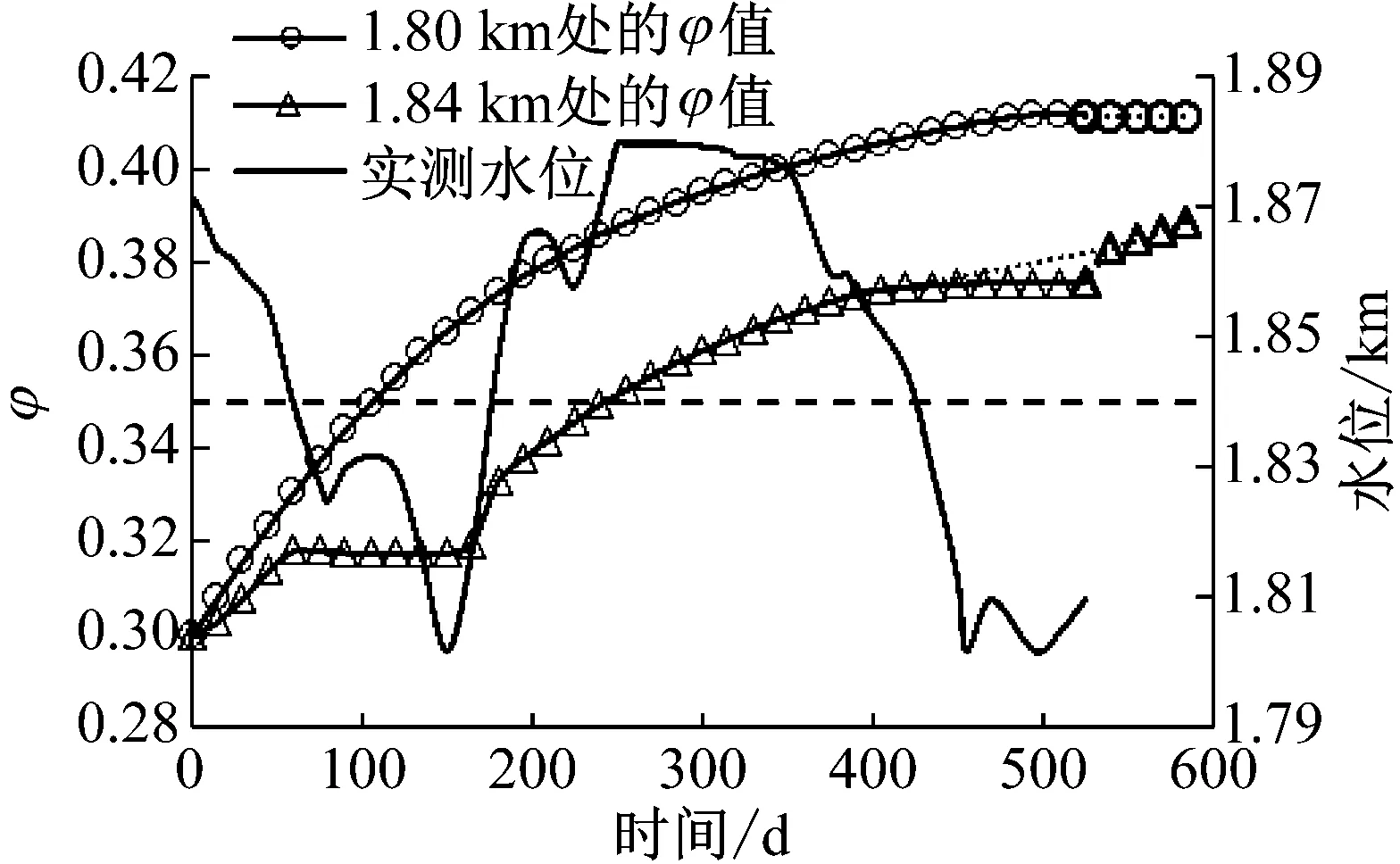
圖5 滑坡體內可被侵蝕顆粒體積分數的變化

圖6為庫水位對內侵蝕速率qe的影響規律。從圖中數值模擬結果可以看出，由于初始孔隙率的存在，臨界粒徑rmin的顆粒很容易通過土體內部原有的孔隙被水流沖刷帶出，所以在內侵蝕發生的初期的0～30 d內，內侵蝕速率是增加的。從總的趨勢來看，隨著細顆粒不斷被侵蝕，可被侵蝕的顆粒越來越少，內侵蝕速率是持續下降的，直到所有可被侵蝕的顆粒被侵蝕完之后，內侵蝕速率變為0，內侵蝕過程結束。其中，在75～165 d及405 d以后，1.84 km高程處的水位是低于1.84 km的，此時的內侵蝕速率為0，滲透率k和可被侵蝕顆粒的φ保持不變，這與圖4和5中表現的規律是一致的。本文所考慮的內侵蝕速率是由可被侵蝕但仍未被侵蝕的顆粒含量決定的，同一時間，高程越低的地方受庫水影響的時間就越長，被侵蝕顆粒的量越多，可被侵蝕但還未被侵蝕的顆粒就越少，導致內侵蝕速率越來越小，故在圖6中體現出的是在同一時間下，絕對水位是一定的，高程高的地方，由于受庫水的影響時間少，未被侵蝕的顆粒含量仍很高，故內侵蝕速率較高程低的地方大。

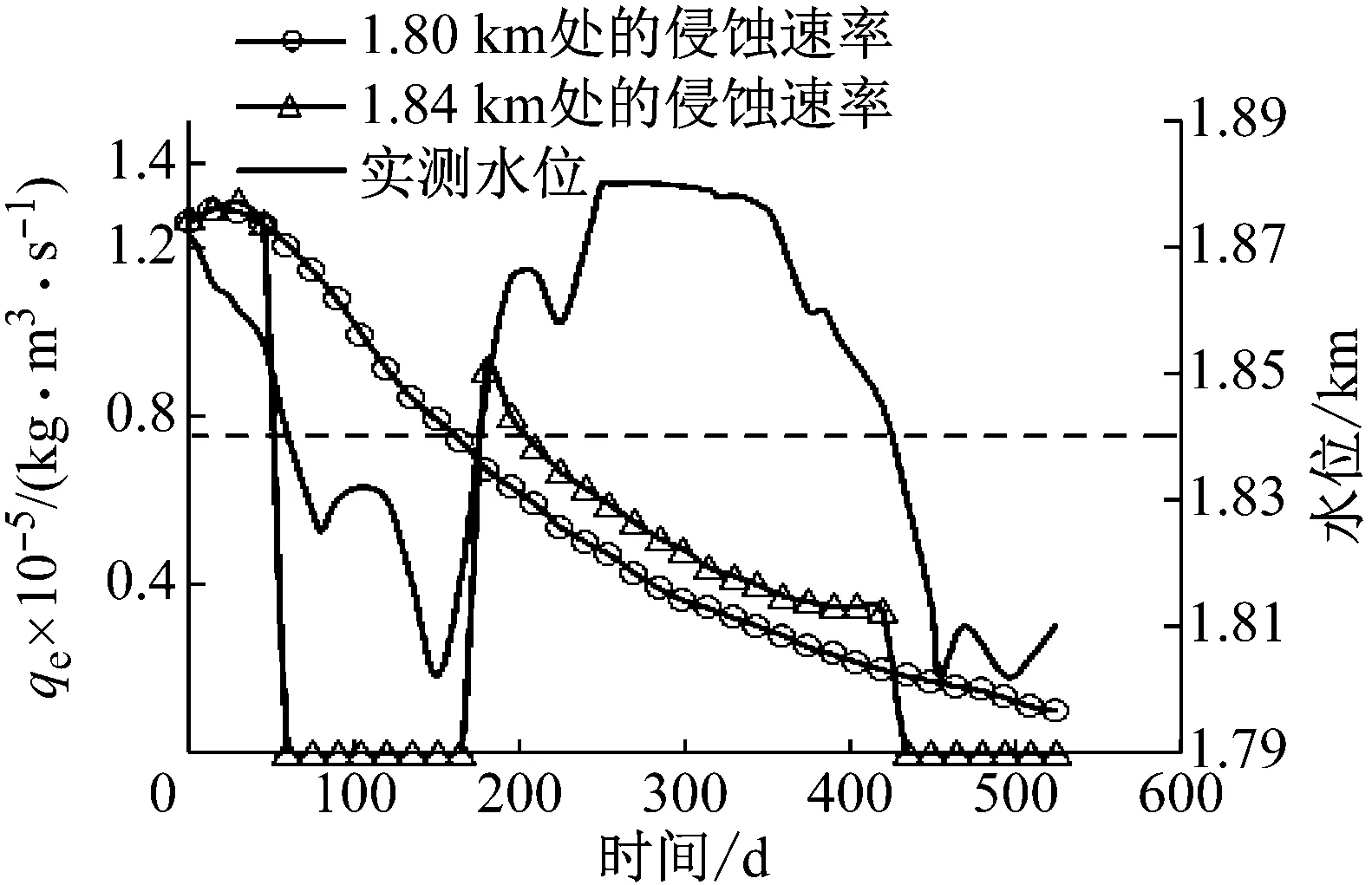
圖6 內侵蝕速率的變化

4 結 論

本文對庫水位作用下土體內侵蝕特性進行了研究，總結如下：

(1) 根據質量守恒方程，建立連續性方程、滲流方程和內侵蝕速率。初步考慮土體的顆粒級配對內侵蝕影響，以可被侵蝕的最小顆粒粒徑rmin和可被侵蝕的最大顆粒粒徑rmax來控制受內侵蝕作用影響的范圍。當rrmin時，則細顆粒有可能被侵蝕出來。

(2) 以錦屏呷爬滑坡滑體為研究對象，利用COMSOL Multiphysics軟件建立有限元模型，耦合上述土體內侵蝕過程中被侵蝕顆粒的質量守恒方程、內侵蝕的滲流方程和考慮級配影響的內侵蝕速率。模擬結果表明土體孔隙率和被侵蝕顆粒的體積分數在內侵蝕作用下不斷增加，當所有可被侵蝕的顆粒都被沖刷掉之后，細顆粒的流失速率最終趨于穩定。而且某一高程處的內侵蝕作用會在水位低于此處高程時暫時停止，當水位重新超過此處高程時，內侵蝕作用會繼續沿著原來的趨勢進行下去。但是該模型未考慮非達西流情況下，即滲透速率與水力梯度呈現非線性增長時的變化情況，以及未考慮水位變化速率的影響。

(3) 該呷爬滑坡的前緣長期處于水下，數值模擬結果顯示處于水下的部分始終受到內侵蝕的影響，細顆粒在不斷的流失，孔隙率持續增大，直至滑坡失穩。因此本文的研究可以用于大致確定滑坡體正處于內侵蝕的哪個階段和水下部分的細顆粒流失程度，對實時監測滑坡的穩定性有一定的實際意義。