無向雙環網絡的強彩虹連通性
劉 杰,陳寶興
(1.閩南師范大學計算機學院,福建 漳州 363000;2.三明醫學科技職業學院,福建 三明 365000;3.數據科學與智能應用福建省高等學校重點實驗室,福建 漳州 363000)
令G為一個非平凡的連通圖,連接圖G中的兩個頂點u和v的最短路徑的長度稱為u和v之間的距離,記為d(u,v).圖G中任意兩個頂點之間距離的最大值稱為圖G的直徑,記作D(G).在G上定義一個邊染色C:E(G)→{1,2,…,k},k∈N,其中相鄰的邊可能染同種顏色,如果一條路P上的邊分別染不同的顏色,則稱P是一條彩虹路.如果圖G任意兩個不同頂點之間都有一條彩虹路相連,則稱圖G是彩虹連通的.使得圖G彩虹連通所需要的最少顏色數稱為G的彩虹連通數,記為rc(G).如果圖G的任意兩個不同頂點之間都有一條最短路徑是彩虹路,則稱圖G是強彩虹連通的.使得圖G強彩虹連通所需要的最少顏色數稱為G的強彩虹連通數,記為src(G).
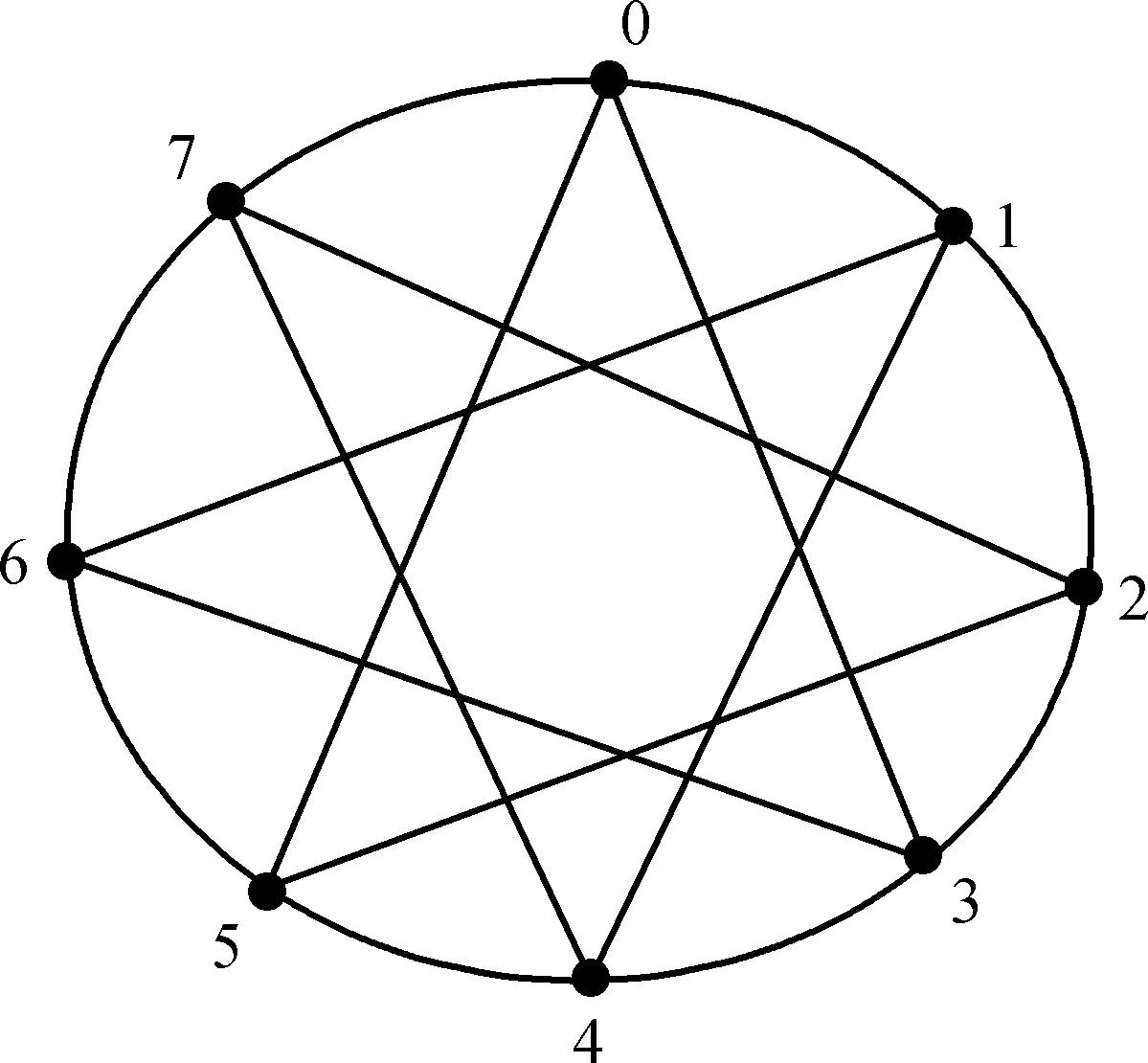
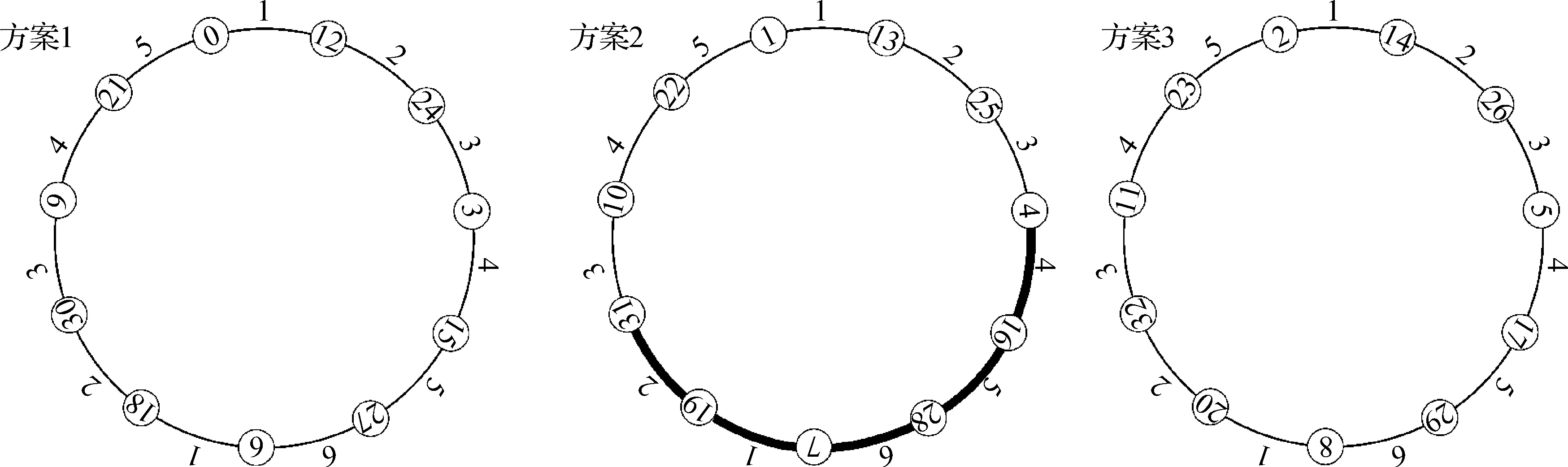
圖的染色有廣泛的實際應用,比如說學生選課系統、電路布局、排序問題、會議安排、電路安排、考試安排等,這些問題都與圖的染色理論密切相關.雙環網絡是一種重要的計算機網絡,它具有對稱性,且易于擴展.與環狀網絡比較,它的直徑比較小,且有較好的容錯能力.雙環網絡在設計和構建大中型網絡或者并行處理計算機系統中有著廣泛的應用.雙環網絡的直徑估計與計算[1-5],構造最優雙環網絡,以及雙環網絡的尋徑策略研究,曾經受到不少學者的重視[6-10].在過去的幾年里,圖的彩虹連通著色[11-13]作為圖論中的一個新問題受到了廣泛的關注,它也被應用到網絡信息安全與密碼學等領域.劉欣欣等[14]給出了有向雙環網絡彩虹連通的一個著色方案,從而得到了其彩虹連通數的一個上界.王燕等[15]研究了一類線性多邊形鏈的彩虹連通著色.本文中將對無向雙環網絡任意兩點之間的最短路徑進行刻畫:證明任意兩點之間存在一條最短路徑W[+s1]+R[+s2],這里|W| 設1≤s1 圖1 無向雙環網絡G(8;±1,±3)Fig.1 Undirected double loop network G(8; ±1, ±3) 對于雙環網絡G(n;±s1,±s2),從點i到點(i+s1) (modn)的邊稱為[+s1]邊,點i到點(i-s1)(modn)的邊稱為[-s1]邊.點i到點(i+s2)(modn) 的邊稱為[+s2]邊,點i到點(i-s2)(modn) 的邊稱為[-s2]邊.若一條從點i到點j的路徑包含x1條[+s1]和x2條[-s1]邊,y1條[+s2]邊和y2條[-s2]邊,則有j≡(i+x1s1-x2s1+y1s2-y2s2)(modn),且等式成立與路徑中邊的順序無關,將此路徑記為:x1[+s1]+x2[-s1]+y1[+s2]+y2[-s2]. 設i、j是G(n;±s1,±s2)中的兩個節點,x1[+s1]+x2[-s1]+y1[+s2]+y2[-s2]是一條從i到j的最短路徑,則x1與x2至少有一個為0,y1與y2至少一個為0.從i到j的最短路徑使用的邊僅含[+s1]與[+s2]或僅含[-s1]與[+s2],或僅含[+s1]與[-s2]或僅含[-s1]與[-s2].從i到j的最短路徑可記為:x[+s1]+y[+s2],這里x、y∈Z. Chen等[4]給出了由G(n;±s1,±s2)所確定的同余方程最小非負解和最小交叉解的定義,并給出了G(n;±s1,±s2)的直徑公式. 定義1[4]稱格點(a1,a2)為同余式 xs1+ys2≡0(modn) (1) 的一個非負解,如果a1s1+a2s2≡0(modn),a1,a2∈Z+,并且(a1,a2)≠(0,0). 稱(u,v)為同余式(1)的最小非負解,若它滿足以下條件: (i) (u,v)為同余式(1)的非負解. (ii) 同余式(1)的任意非負解(a1,a2),都有u+v≤a1+a2. (iii) 如果存在同余式(1)的非負解(a1,a2)≠(u,v)并且a1+a2=u+v,則有u>a1. 定義2[4]稱格點(-a1,a2)為同余式(1)的交叉解,如果-a1s1+a2s2≡0(modn),a1、a2∈Z+,(-a1,a2)≠(0,0),并且(-a1,a2)、(0,0)、(u,v)三點不在同一直線上,其中(u,v)為同余式(1)的最小非負解. 稱(-a,b)為同余式(1)的最小交叉解,若它滿足以下條件: (i) (-a,b)為同余式(1)的交叉解. (ii) 同余式(1)的任意交叉解(-a1,a2),都有a+b≤a1+a2. (iii) 如果同余式(1)存在交叉解(-a1,a2)≠(-a,b)并且a+b=a1+a2,則有b>a2. 引理1[4]設(u,v)、(-a,b)分別是同余式(1)的最小非負解和最小交叉解.如果u≥v,則有a≤u、a≤b、v 特別地,容易證明:如果u=v,則有a 引理2[4]設(u,v),(-a,b)分別是同余式(1)的最小非負解和最小交叉解.如果u 引理3當u=v時,對于0≤k≤n-1,G(n;±s1,±s2)中存在一條從0到k的最短路徑W[+s1]+R[+s2],滿足|W| 證明對于0≤k≤n-1,若W[+s1]+R[+s2]是一條從0到k的最短路徑,則必有|R| 用反證法,若|R|≥b,不妨設R≥b(R≤-b類似可證).由引理1可知,當u=v時,有a 若|W|≥u,不妨設W≥u(W≤-u類似可證).設W=iu+j,這里i、j∈Z,且0≤j≤u-1.注意到(W-iu)[+s1]+(R-iu)[+s2]也是一條從0到k的路徑,且|W-iu|+|R-iu|=W-iu+|R-iu|≤W-iu+|R|+iu=W+|R|.因此(W-iu)[+s1]+(R-iu)[+s2]也是一條從0到k的最短路徑且|W-iu| 引理4當u>v時,對于0≤k≤n-1,G(n;±s1,±s2)中存在一條從0到k的最短路徑W[+s1]+R[+s2],滿足|W| 證明對于0≤k≤n-1,若W[+s1]+R[+s2]是一條從0到k的最短路徑,則必有|W| 用反證法,若|W|≥u,不妨設W≥u(W≤-u類似可證).注意到(W-u)[+s1]+(R-v)[+s2]也是一條從0到k的路徑,且|W-u|+|R-v|=W-u+|R-v|≤W-u+|R|+v<|W|+|R|,這與W[+s1]+R[+s2]是一條從0到k的最短路徑矛盾. 若|R|≥b,不妨設R≥b(R≤-b類似可證).設R=ib+j,這里i、j∈Z,且0≤j≤b-1.注意到(W+ia)[+s1]+(R-ib)[+s2]也是一條從0到k的路徑,且|W+ia|+|R-ib|=|W+ia|+R-ib≤|W|+ia+R-ib≤|W|+|R|,因此(W+ia)[+s1]+(R-ib)[+s2]也是一條從0到k的最短路徑且|W+ia| 引理5當u 證明對于0≤k≤n-1,若W[+s1]+R[+s2]是一條從0到k的最短路徑,則必有|W| 用反證法,若|W|≥a,不妨設W≥a(W≤-a類似可證).注意到(W-a)[+s1]+(R+b)[+s2]也是一條從0到k的路徑,且|W-a|+|R+b|=W-a+|R+b|≤W-a+|R|+b<|W|+|R|,這與W[+s1]+R[+s2]是一條從0到k的最短路徑矛盾. 類似可證|R| 令t1=max{u,a},t2=max{v,b},從引理3~5,可得引理6. 引理6對于0≤k≤n-1,在G(n;±s1,±s2)中存在一條從0到k的最短路徑W[+s1]+R[+s2]滿足|W| 無向環狀網絡G(n; ±s)是如下定義的無向圖(V(G),E(G)):節點集V(G)={0,1,2,…,n-1},邊集E(G)={i→i-s(modn),i→i+s(modn)|i=0,1,2,…,n-1}.注意到G(n;±s)是連通的當且僅當gcd(n,s)=1.當gcd(n,s)=d>1時,無向環狀網絡是不連通的.此網絡有d個連通分量,節點0,1,2,…,n-1分別屬于這d個連通分量. 引理8的證明與文獻[14]的引理1類似,這里略去. 例1對于無向環狀網絡G(33;±12),取t=5,則用6種顏色對G(33;±12)邊著色,就可使得G(33;±12)中任一條長度不超過5的路徑均是一條彩虹路. 下面將給出無向雙環網絡強彩虹連通的一個著色方案,并給出了該網絡強彩虹連通數的一個上界. 圖2 環狀網絡G(33;±12)的彩虹著色方案Fig.2 The rainbow coloring scheme of loop network G(33;±12) 證明注意到無向雙環網絡的邊有兩種類型:一種是[+s1]邊或[-s1]邊,即G(n; ±s1)中的邊,另一種是[+s2]邊或[-s2]邊,即G(n;±s2)中的邊. 這樣便完成了無向雙環網絡G(n; ±s1,±s2)中所有邊的著色. 據引理6,對于0≤k≤n-1,在G(n;±s1,±s2)中存在一條從0到k的最短路徑W[+s1]+R[+s2]滿足|W| 在G(n;±s1)中有一條長為|W|的彩虹路:當W>0時,0→s1→2s1→…→Ws1.當W<0時,0→-s1→ -2s1→…→Ws1. 在G(n;±s2)中有一條長為|R|的彩虹路:當R>0時,Ws1→Ws1+s2→Ws1+2s2→…→Ws1+Rs2.當R<0時,Ws1→Ws1-s2→Ws1-2s2→…→Ws1+Rs2. 因在兩個網狀網絡G(n;±s1)與G(n;±s2)中的著色不同,故可得到一條從0到k,長度為|W|+|R|的最短彩虹路.證畢. 證明僅就u≥v的情形給出證明,u 當u≥v,r3=r4且(u+a)(v+b)≡1(mod 2)時,可推出a=v.由引理1,可知a≤u.因此r3=(u+b)/2.據引理7,可得D(G)=r3-1=(u+b)/2-1.由定理1,可知src(G)≤2(t1+t2)-6=2(u+b)-6=4[(u+b)/2-1]-2=4D(G)-2.證畢. 例2求無向雙環網絡G(2t2+2t+1;±1,±(2t+1))(這里t是正整數,t>1)的強彩虹連通數的上界、直徑. (ii) 計算G(2t2+2t+1;±1,±(2t+1))的直徑. 注意到src(G)≥D(G),我們得到的G(2t2+2t+1;±1,±(2t+1))的強彩虹連通數上界2t+2與該網絡直徑t較為接近. 圖的彩虹著色問題是一個多項式復雜程度的非確定性(NP)問題.其困難在于使用最小顏色數k,并要求G的任意兩點間均有一條彩虹路.直至目前,未見有文獻給出無向雙環網絡的彩虹著色方案.本文中通過對無向雙環網絡任意兩點之間的最短路徑進行刻畫,進而給出了該網絡強彩虹連通的一個著色方案,最后得到了該網絡強彩虹連通數的一個上界,這上界主要由G(n;±s1,±s2)所對應的同余方程的最小非負解和最小交叉解中的4個參數表示.下一步的任務是找出更好的著色方案,使得所用的顏色數更少.1 定義及引理



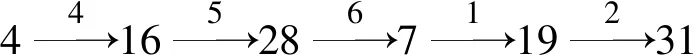
2 主要結果







3 結 論

