基于插值細分的機械臂手眼標定算法

黃騰超，陳默含，馮勇建，夏榮菲

(廈門大學航空航天學院，福建 廈門 361102)

機器視覺搭配機械臂的開發應用具有自動化、精密化、智能化等特點，近年來被廣泛應用于工業生產中.手眼標定作為機器臂匹配視覺系統必不可少的一環，其算法的精確性、穩定性和高效性決定了機械臂在工業生產中的適用性和智能化程度.然而，傳統標定算法[1-4]通常是對已知規格標定板上的特征點進行二維圖像坐標與三維空間坐標定位，通過計算得到相機焦距、畸變系數、像素實際大小、圖像主點等內部參數(內參)，以及相機三維旋轉角度和偏移量等相機位姿外部參數(外參).利用相機內參對畸變模型的泰勒級數展開進行擬合，得到消除畸變的真實圖像信息;再將真實圖像與外參構建的旋轉矩陣和平移矩陣進行矩陣耦合運算，確定相機坐標系與世界坐標系的關系.這種算法雖然可以適用于大多數相機標定，但是其標定精度完全依賴初始的相機內參以及旋轉矩陣和平移矩陣的求解.相機焦距、畸變系數、旋轉矩陣和平移矩陣對于標定板的規格選擇以及視覺主點的定位精度要求極高，而這些參數在求解過程中容易出現誤差.在大視場的環境條件下，相機內、外參數的求解稍有誤差，便對最后的標定精度影響很大.同時，傳統標定算法因為對矩陣求解速度的考量，僅考慮二階以內的徑向畸變，使得在畸變較小與較大的區域內，擬合的畸變模型無法完全匹配固有存在的高階畸變，從而使標定結果出現不穩定的情況，導致無法預測的誤差.在實際運用中，像素為千萬級的相機在采用傳統算法對1.5 m×0.75 m的工作平面進行標定時，誤差精度一般在3～6 mm之間[5]，無法滿足工業生產的精密性要求.

針對傳統標定算法的不足之處，本文中提出一種基于插值細分和運動限制的固定視點下的手眼標定算法.該算法利用機械臂做縱向與橫向的自動增量運動，對目標區域的位置信息進行采集，并細化標定區域，通過插值逼近算法擬合畸變曲線，使得標定平面的像素坐標系與機械臂基坐標系實現一一對應的轉換關系，從而實現高精度的手眼標定.

1 標定原理

1.1 相機標定原理

機器視覺處理定位問題時的關鍵在于從相機獲取目標圖像的信息中計算出三維空間物體的幾何信息，以此對圖像中的目標進行重構和識別.由于空間中點的三維幾何位置與其在圖像中的對應點之間的相互關系是由相機的成像模型決定的，所以在標定過程中，標定平面的選取和對成像模型的計算決定了標定精度的水平.機器視覺系統中的手眼標定是為了獲取圖像坐標系(xc,yc,zc)與機械臂基坐標系(xr,yr,zr)以及世界坐標系(xw,yw,zw)三者之間的轉換關系.如圖1所示，O為圖像主點，Cx、Cy為主點圖像坐標，Sx、Sy為像素在世界坐標系的實際大小.在進行手眼標定時，若機械臂的坐標系固定，且具有較高的精度和穩定性，可以將世界坐標系與機械臂基坐標系二者作為一個整體進行考慮，即直接尋求圖像坐標系與機械臂基坐標系之間的轉換關系[6].

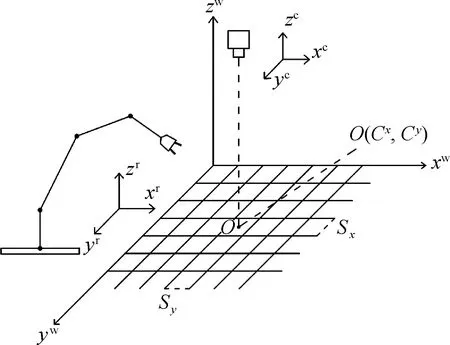
圖1 坐標轉換關系Fig.1 Coordinate transforming relations

1.2 相機畸變模型

相機鏡頭上光學透鏡固有的透視失真引起的圖像畸變常見的有徑向畸變和切向畸變.但研究表明[7-9]，在校正模型中引入過多的畸變校正參數，可能會增加計算的復雜性，導致計算結果不收斂而得不到高精度的標定.一般情況下，相機的切向畸變主要是因為鏡頭透鏡與成像平面不平行而產生的，鏡頭模組上的安裝偏差，會導致采集圖像平面的偏斜.但是在實際操作中，保持鏡頭與工作平面近乎水平的條件下，就可以避免明顯的切向畸變產生.因此，在鏡頭與工作平面近乎水平的條件下，引入切向畸變模型，不僅對提高手眼標定精度的作用不大，而且反而會增加計算的復雜性，導致計算結果不收斂[10].因此，本文中只考慮徑向畸變模型.

徑向畸變[11]是沿著透鏡半徑方向分布的畸變，產生原因是經過透鏡的光線發生不同程度的偏折，而導致圖像點在遠離主點的地方比靠近主點的地方產生更大的徑向位移.如圖2所示，根據產生徑向位移的正負向關系，徑向畸變又分為桶形畸變和枕形畸變.

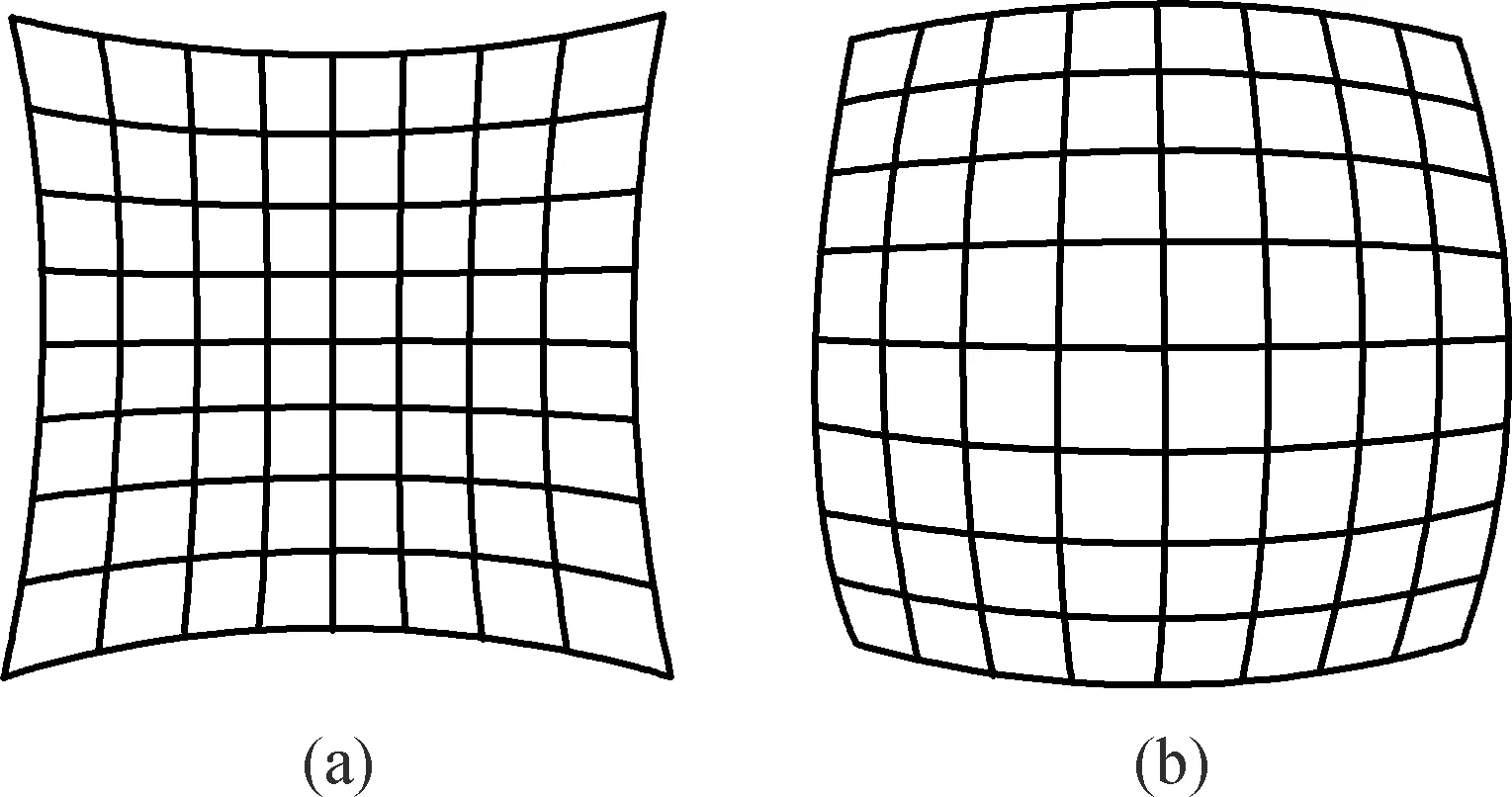
圖2 枕型畸變(a)和桶型畸變(b)Fig.2 Pincushion distortion (a) and barrel distortion (b)

從圖2可知，徑向畸變成像光軸中心不產生畸變，沿著鏡頭圓心向邊緣移動，畸變越來越嚴重.畸變的數學模型可以用主點周圍的泰勒級數展開式的前幾項進行描述，通常取前兩項，對于畸變嚴重的鏡頭取3項或者更多項.張氏標定法[12-13]提出，畸變圖像上某點的像素點坐標可表示為：

xu=xd+(xd-xo)(k1rd+k2rd2+…),

yu=yd+(yd-yo)(k1rd+k2rd2+…).

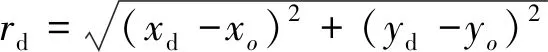
2 基于插值細分的手眼標定方法

通過上述對畸變模型的分析可知，影響標定精度的因素主要為由光學透鏡造成的徑向畸變影響，而徑向畸變可以通過泰勒函數展開式逼近來描述;但是在實際工作中，只能在誤差允許的范圍內取有限階，通過高階泰勒函數逼近的徑向畸變模型只能近似于真實的徑向畸變.因此，泰勒多項式階數的選取對于畸變模型的還原起到至關重要的作用.但是，在實際操作中，依靠高階泰勒多項式來還原采集圖像中的徑向畸變，會降低標定算法的運算速度，無法達到實際運用中高效、精確的需求.

因此，在處理徑向畸變的標定模型上，本文中提出一種基于密集標定點的插值細分算法.插值細分算法易于產生性能良好的曲線曲面，且具有簡潔高效和計算速度快等優點，符合手眼標定中快速、精確的需求.

2.1 插值細分原理

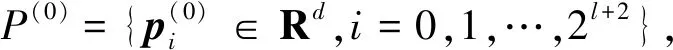
其中，ω=1/16的極限曲線有較好的連續性.對于控制頂點集的控制點進行相同的細分規則，獲得新的插值點，循環往復，通過l次細分，便可獲得2ln+1個插值點.如圖3所示，以曲線①中5點為控制頂點集，通過對控制集進行一次插值可得到9個插值點構成的曲線②，然后再以曲線②中各點作為控制頂點集，進行二次插值則可獲得17個插值點構成的曲線③.根據插值細分法的定理可知這些插值點收斂于一條極限曲線上[16].

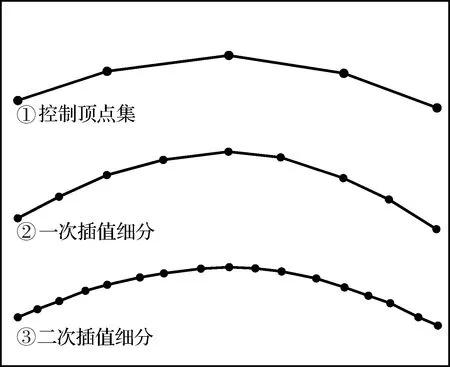
圖3 插值逼近示意圖Fig.3 Diagram of interpolation approximation

插值細分在細分過程中每一步都不會改變舊控制點的位置，故在用插值逼近畸變曲線處理徑向畸變的過程中，插值曲線經過每一次細分過程生成的控制點并不替代原控制點的位置，保證曲線的真實性.

2.2 插值點生成

生成標定點控制頂點集，首先要對標定平面的標定點進行采集，如圖4(a)所示，將易識別的標定特征圓架接于機械臂末端，并控制機械臂做自動增量位移，可以遵循先橫后縱的遍歷方式.機械臂每次位移2 cm，同時，用相機抓拍每一次位移的特征圓位置，利用圖像處理立即定位出標定特征圓的圓心圖像坐標，并訪問機械臂回傳參數，記錄下每次位移的機械坐標，采集到的點如圖4(b)所示.

圖4 標定平面的標定點采集Fig.4 Calibration point acquisition of calibration plane

由畸變模型可知，圖像中水平直線和豎直直線上的徑向畸變曲線較為齊整，不會出現明顯偏折.因此，根據四點插值算法的細分規則，可對采集的標定點進行細分，便可還原現實中在直線上的點對應于圖像上的畸變點.具體細分的步驟如下所述：

1) 將采集到的圖像坐標細分為若干個5×5的方塊，每個方塊都可被定義為

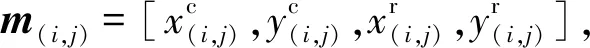
2) 然后按行進行提取，則可獲得5個點構成的控制集

Pi(0)={m(i,0),m(i,1),m(i,2),m(i,3),m(i,4)}，(i=0,1,…,4).

3) 根據插值細分原則，對5個控制集進行3次插值，取第一行為例：

經過3次插值，每個控制集均可細分為出33個插值點

(i=0,1,…,4).

4) 將擴充的插值點重新歸納，則原矩陣擴充為5× 33的矩陣

5) 同理，對新矩陣M1的列進行插值細分，則有新的33個控制集數

Pj(0)={m(0,j),m(1,j),m(2,j),m(3,j),m(4,j)},

(j=0,1,…,32),

繼續進行細分，則可得擴充后的33×33矩陣

因為對應標定點之間距離較小，所以，經過插值算法，可生成一個間距幾近相同的密集點陣，其中每個點都包含圖像坐標與機械臂基坐標系，為方便調用可保存于矩陣文件中.

由標定原理可知，手眼標定的關鍵在于如何求出機械臂基坐標系與圖像坐標的轉換關系，根據微分原理可知，通過多次細分后，每個插值點之間的曲線可近似于直線.由于相機畸變模型的曲線較為平緩，所以可以將3次細分后的密集標定點陣切分為1 029個2×2的區域點陣，如圖5，每個點陣內區域可用線性關系求解.

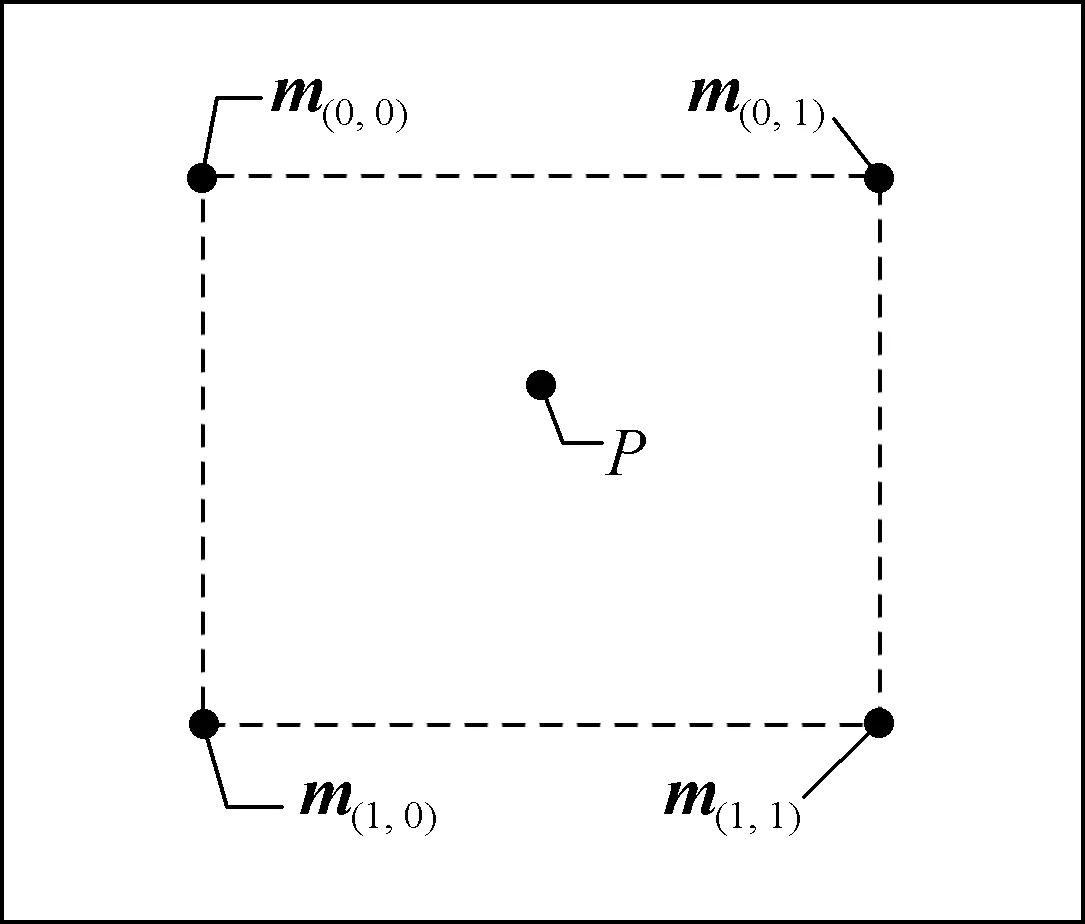
圖5 目標點落點定位Fig.5 Location of object points

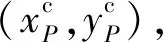
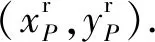
3 實驗結果和分析

圖6 實驗裝置圖Fig.6 Experimental equipment

本次實驗所用的機械臂型號為安川MOTOMAN-MH24機械臂，相機型號為海康威視MV-CE100-30GM面陣相機，易識別的特征圓點直徑為4 cm，采集平面約為150 cm×70 cm，圖像大小為3 840像素×2 748像素，具體實驗裝置圖如圖6所示.此外，利用HALCON編寫特征點識別程序，并通過Visual Studio 2017編寫控制界面，兩者聯用完成數據采集和處理.

3.1 手眼標定實驗

根據不同區域的畸變程度不同共設計3次實驗，每次分20組，共采集200個標定點進行標定誤差計算.第一次實驗隨機選取20個區域，讓機械臂在標定區域內自由移動，每個區域取10個目標點，計算平均誤差.此外，為驗證插值算法擬合畸變的準確性，設計第二次實驗隨機選取圖像邊緣畸變較大區域，而第三次實驗隨機選取圖像中心附近畸變較小區域.同第一次實驗一樣，第二、三次實驗每次也取20個區域，每個區域取10次目標點.

同時，以傳統標定算法作為對照組進行實驗，其標定模板如圖7所示.傳統標定算法主要通過標定模板計算相機內部焦距、畸變系數等參數還原畸變圖像，再利用外部旋轉矩陣和平移矩陣矯正相機位姿，從而將相機坐標系與世界坐標系聯系起來.此次傳統標定算法中的相機內、外參數由HALCON自帶標定程序計算得出，參數詳見表1.

圖7 標定模板圖Fig.7 Calibration target

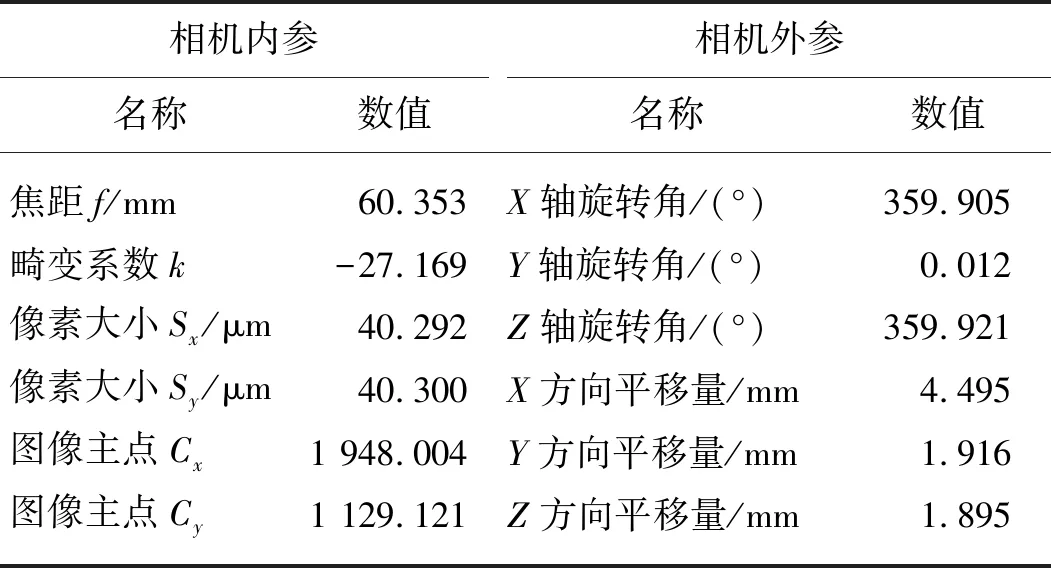
相機內參相機外參名稱數值名稱數值焦距f/mm 60.353X軸旋轉角/(°)359.905畸變系數k-27.169Y軸旋轉角/(°)0.012像素大小Sx/μm40.292Z軸旋轉角/(°)359.921像素大小Sy/μm40.300X方向平移量/mm4.495圖像主點Cx1 948.004Y方向平移量/mm1.916圖像主點Cy1 129.121Z方向平移量/mm1.895

利用機器臂末端的特征點在固定標定平面上不規則的增量運動，通過比對機械臂回傳的自身位置坐標和圖像識別轉換后的位置坐標，計算出標定算法的實際誤差.設機械臂回傳的真實位置坐標為(xr,yr)，根據圖像坐標轉換的位置坐標為(xt,yt)，用二維歐幾里得距離E來表示誤差，則

上述的誤差是機械臂基坐標系上的誤差，機械臂每位移一次，相機采集一次圖像，比對機械臂回傳的位置坐標和圖像識別轉換位置坐標計算一次實驗誤差，設n為采集次數，定義平均誤差?為：

3.2 實驗數據和誤差分析

通過平均誤差計算公式，對實驗數據進行標定精度的誤差分析，即將實驗采集數據代入誤差公式.通過對兩種標定方法在不同標定區域的平均誤差計算，根據所得數據整理得出圖8.由圖8可知，插值細分法的誤差曲線較為平穩，而傳統標定算法的誤差曲線穩定性較差.插值細分法的誤差幾乎都在1 mm以內，而傳統標定方法誤差分布在1.5～5 mm之間，插值細分法標定精度明顯更高.

圖8 平均標定誤差Fig.8 Average calibration error

此外，由圖8中傳統標定法和插值細分算法在全區域的誤差曲線可以看出，6到13組的誤差明顯高于其他組.經分析，其原因是6到13組的測試點都選取在圖像畸變嚴重的圖像邊緣.而對比圖8(a)和圖8(b)中邊緣區域與中心區域的標定誤差可發現在畸變嚴重區域，兩種標定方法的平均標定誤差明顯增大.但傳統標定算法平均誤差高達5 mm，且十分不穩定.而插值細分法，雖在畸變明顯的區域誤差略有增大，但其最高誤差不超高1 mm，平均誤差基本穩定在0.3 mm.實驗證明基于差值細分的標定方法可以，其標定精度滿足實際的工程運用.

圖9中(a)～(d)為插值算法運用在工業點膠機械臂上的實際效果圖.圖9(a)為圖像處理的工件邊框效果圖，通過對工件邊框進行識別定位得到工件邊框的圖像坐標，然后由插值標定算法的坐標轉換將圖像坐標轉換成機械坐標，并將數據傳給機械臂.圖9(b)～(d)為實際機械臂在工件邊框涂膠的效果圖，可以看出，膠槍走的路徑與圖像識別規劃的邊框路徑基本一致.

圖9 實際應用效果圖Fig.9 Practical application effectiveness

4 結 論

根據實驗結果和實際應用效果，針對固定視點的手眼標定系統，本文中提出的基于差值細分算法的標定方法不僅能夠簡單快速地完成標定工作，還能減少傳統算法中存在的標定誤差，標定精度在1 mm以內.該方法通過機械臂的自動位移解決傳統標定算法中求取相機內、外參數的繁瑣步驟，改進了目標點圖像坐標系和機械臂基坐標系之間的轉換方式，使標定更加便捷、易操作，符合現代工業生產高效率、高精度的需求.