用“變”與“不變”思想進行數學復習

王少平

摘? ?要：數學是運動變化的，且在運動變化中顯示“變”與“不變”的獨特魅力，彰顯其內在的規律性，體現知識間的前后聯系。“變”與“不變”作為一個重要的數學思想應在學生的數學學習中予以滲透，以便學生領悟并能運用知識間的聯系建構系統的知識網絡。在復習課中滲透“變”與“不變”思想，有利于學生發現知識間的聯系，對知識進行整理和重組，將“變”與“不變”思想轉化為解決問題的一種模式，利于知識的保持、遷移和運用，從而促進數學思維提升，提高問題解決能力。

關鍵詞：小學數學;數學復習;“變”與“不變”;教學策略

中圖分類號：G623.5? ? 文獻標識碼：A? ? 文章編號：1009-010X（2019）28-0021-03

“萬物皆變”，這是哲學基本理念。既有“變”，就有“不變”。在數學中以“變”與“不變”為主線，鎖定主要教學內容，既有利于創設良好的認知環境，又能讓學生多一些哲學高度的思考。拿數學復習課來說，復習課的主旨就在于讓學生透過變化的情境和信息去抓住其中不變的本質。復習課上利用“變”與“不變”的關系引導學生透過現象看本質，讓其立足哲學的視野進行理性地思考：體悟、描述“變”與“不變，探尋、應用“變”與“不變”。促使他們養成對事物、對生活的態度：千變萬化的事物存在怎樣的聯系？這些聯系可以幫助我們有哪些新發現？這樣的復習課讓學生從繁雜的機械訓練中走出來，借助數學問題、數學關系、數學特點吸引學生，建構清晰的知識網絡，讓數學復習課煥發出應有的數學魅力。

再者，復習課中教師本應幫助學生建立起一個具有聯系性的知識體系，使之成為個人內部知識網絡的一部分，這樣才更利于學生知識的長久保持、遷移和運用。然而，很多教師在上復習課時總是占用大量時間讓學生回憶“學習了哪些知識”，讓其在帶有明確指向性的問題牽引下，將已學的知識點一一說出。在這種復習中，知識點之間的聯系主要表現為線性的、單向的，無法建立完善的認知結構，無法讓學生的思維向縱深處發展，且像這種碎片化的知識點羅列，會阻礙知識的深度理解和遷移運用。

本文以小學數學六年級“立體圖形的復習”為例，談一談教師如何從“變”與“不變”的角度引導學生展開空間推理，尋找新舊知識間的內在關聯;如何在“變”中尋求“不變”，促進知識的整理和重組，建構立體的知識網絡;如何抓住“不變”探尋解決問題的思路，構建問題解決的策略，提升數學思維品質。

一、在運動變化中引發聯想，體悟“變”與“不變”

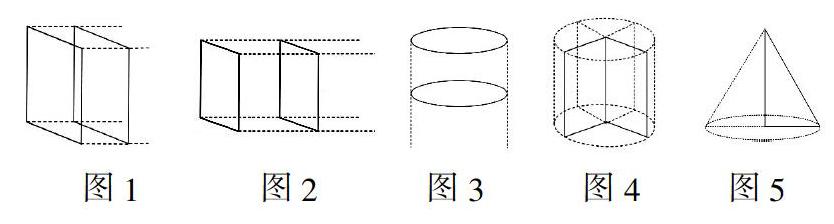
【案例描述】教師用PPT出示長方體、正方體、圓柱體、圓錐體這幾個立體圖形，提問：這幾個立體圖形分別可以用什么樣的平面圖形通過何種運動方式轉化而來？立體圖形與平面圖形之間有什么聯系？學生思考回答并結合PPT的動態演示，借助透視圖（見下圖）進行空間想象，

并語言描述：平面圖形經平移或旋轉運動后，其運動軌跡形成了一個立體圖形，平面圖形成了立體圖形的一部分。并且原來的平面圖形與轉化后的立體圖形之間存在著諸多聯系。圖1：長方形成了長方體中的一個側面，長方形的長成了長方體的高，長方形的寬成了長方體的寬，長方形的面積成了長方體側面（左或右）的面積，長方形向右平移的距離就是長方體的長;圖2：原來的正方形成了正方體中的一個面，正方形向右平移的距離等于正方體的棱長，正方形的邊長與正方體棱長相等;圖3：圓向下平移的距離就是圓柱體的高，圓成了圓柱體的底面，圓的半徑就是圓柱體的底面半徑;圖4：原來長方形的長成了圓柱體的高，長方形的寬成為了圓柱體的底面半徑，長方形的面積是圓柱體縱切面面積的一半;圖5：直角三角形中作為軸的一條直角邊成了圓錐體的高，另一條直角邊成為了圓錐體的底面半徑，三角形的面積是圓錐體縱切面面積的一半……

【案例評析】 學生通過空間想象與直觀透視圖的觀察，明晰了二維的平面圖形轉化為三維的立體圖形后，圖形的形狀雖然變了，但轉化后的立體圖形并不是孤立的個體存在，而是與原來的平面圖形有著千絲萬縷的聯系。這個“聯系”就是學生在“變”的表象背后所看到的“不變”。這些“不變”的聯系從一維的邊線到二維的平面、再到三維的立體，均在學生的腦中、眼中、口中一一呈現。這一過程既讓學生初步感知了二維的平面圖形轉化為三維的立體圖形后的“變”與“不變”，激發起學生的空間想象，又溝通了新舊知識間的聯系，利于架構一個立體的知識網絡，同時也潛移默化地融入了“數學”是發展變化的這一本質內涵。

二、在操作變化中尋求聯系，描述“變”與“不變”

上一環節是讓學生在運動變化中直觀感知由平面到立體的聯系，這一環節則是結合一定情境將“操作”與“面、體的計算”相融合，讓學生在自主選擇操作方式中實現變式練習，明晰“變”與“不變”相互依存，滲透辯證思想。

【案例描述】師：在學習立體圖形時，我們經常會通過“切”“削”“拼”“熔”的操作，將立體圖形“變形”，從而產生很多新問題。比如：將兩個完全一樣的正方體拼成一個長方體、將一個圓柱體削成一個最大的圓錐體、將一塊正方體形狀的方鋼鍛造熔鑄成一塊圓柱體形狀的鋼柱……變形之后的立體圖形與原來的立體圖形之間有什么聯系？請選擇“切”“削”“拼”“熔”中的一種方法將一個立體圖形變形，然后再說一說變形前后“什么變了，什么沒變？”

學生1：用“削”的辦法，把圓柱削成和它等底等高的圓錐，形狀變了，體積只是原來的三分之一，但底與高不變。

學生2：選用“切”的辦法，在長方體中切出一個最大的正方體，體積變了，但切出的正方體的棱長是原長方體中最短的一條棱的長度。

學生3：采用“拼”的方法，把兩個一樣的正方體拼成一個長方體，形狀變了，長方體的體積是原來正方體的2倍，正方體的面成了長方體中的側面。

學生4：用“熔”的方法，把一個正方體方鋼鍛造成一個長方體，形狀變了，體積沒變。

【案例評析】這一環節中的“切、削、拼、熔……”不僅僅是外在的操作方式，還轉化為用來傳意的工具，學生據此進行表達和交流，靈活運用已有知識進行題型變換，讓學生對立體圖形中“表面積與體積的計算”知識進行了整體回顧與把握。

三、在情境中聚焦“不變”，探尋問題解決的突破口

【案例描述】 教師出示圓柱（圖6），底面直徑4分米，高16分米。出示下列問題：

問題1：把這個圓柱削成一個

最大的圓錐，應該削去多少？

問題2：把這段圓柱沿底面直

徑縱切一刀，表面積增加多少？

問題3：給這個圓柱形拼接上

10分米長的一段，表面積增加多少？

問題4：把它鍛造成一個等底的圓錐，圓錐的高是多少？

師提問，找出每道題中圖形變化前后的聯系，即“不變”的地方，并說說解題的思路。

學生思考后回答，摘錄如下：

問題1：削成的圓錐與圓柱等底等高，所以圓柱體積的■就是削去的量。

問題2：縱切面的長和寬就是圓柱的高和底，16×4×2就是增加的表面積。

問題3：拼接上的底面與圓柱的底面相等，用底面周長乘拼接的長就是增加的表面積。

問題4：圓柱和圓錐的體積與底面積相等，利用圓錐的體積計算公式即可算出圓錐的高。

【案例評析】教師通過設計有聯系的題組，先讓學生尋找問題中“不變”的地方，依托“不變”，挖掘出圓柱變化前后的“聯系”，找到解決問題的思路。尋求“變化”背后的“不變”，才是解決問題的突破口。“變”與“不變”作為一種數學思想已內化為認知思維中問題解決的策略，喚醒了學生解決問題的策略意識。在尋找“變與不變”中，各個知識點也在學生頭腦中連成線、織成網，促成知識結構重組，從而達到復習的目的。

四、應用中內化“變”與“不變”思想，構建解決問題的模型

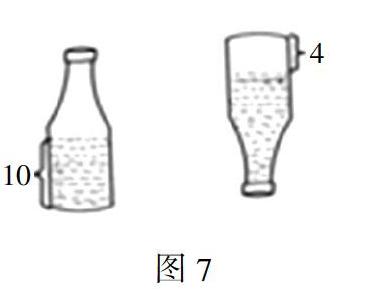
【案例描述】 PPT出示：“將一個玻璃瓶子正立（圖7），底面直徑是8厘米，水的高度是10厘米;再將玻璃瓶倒立，空著部分的高度是4厘米。這個玻璃瓶的容積是多少？”

學生思考交流：不管瓶子是“正立”還是“倒立”，瓶子中水的形狀變了，但是水的體積不變。討論匯報：第一個瓶子中水的體積加上第二個瓶子中空的部分的體積，就是整個瓶子的容積。補充：因為水的體積不變，第一個瓶子中空白部分是不規則的，所以用第一個瓶子中水的體積加上第二個瓶子空的部分的體積。

【案例評析】學生無需教師的指導和點撥，自覺運用“變”與“不變”思想找到了解決問題的思路。在語言表述中學生思路清晰、縝密。顯然，在“變”中尋求“不變”，已作為一種問題解決的策略被學生吸納和運用。在語言表述中學生思維的主動性和嚴謹性無疑是策略意識外化的表現。

縱觀本節課，將“聯系”的觀點貫穿始終，跳出了傳統復習課“單純回憶”的怪圈，也不再是大量的機械訓練，而是讓學生一直在“變”與“不變”中進行理性思辨，打通了一維的邊線、二維的平面和三維的立體圖形間的聯系。學生形成了運用“變與不變”思想解決問題的策略，提升了數學思維品質和解決問題能力。同時，他們學會了運用運動變化的觀點去審視周圍的事物，透過“變化”的表象去深究事物內在的本質聯系，于潛移默化中提升數學素養，這應該是本節課教學的真正價值所在。