基于滑模變結構控制的路徑跟蹤研究

(常州大學 機械工程學院，常州 213100)

0 引言

隨著流化床鍋爐的廣泛應用，預防鍋爐的失效也成為人們研究的熱點[1]，而鍋爐水冷壁的磨損是其主要的失效形式之一[2]。現如今的鍋爐水冷壁磨損檢測主要由人工完成，而人工檢測效率低，費用高且事故易發，所以研制一種智能機器人代替人工作業是現在市場所需求的。

在鍋爐內部，磨損檢測機器人的移動作業環境較為復雜，準確的路徑跟蹤控制是保證其測量結果可靠的關鍵。對移動機器人的路徑跟蹤控制的研究一直是現今機器人研究的熱點。李金良[3]等人在機器人運動原理的基礎上采用線性反饋控制來進行路徑跟蹤，線性反饋控制法是一種常用的路徑跟蹤控制方法，但水冷壁磨損檢測爬壁機器人的模型是非線性的，致使其控制精度較低；陳罡[4]等人根據backstepping(反演法)結合Lyapunov穩定理論設計了一種時變反饋控制律，控制效果不錯，但設計過程較為復雜，很難在實際應用中實現；智能控制的出現使控制器不再局限于數學模型[5]，王紀偉[6]等人提出了一種基于模糊免疫比例積分微分(PID)的智能控制方法，但模糊控制效果依賴于其模糊規則制定的好壞，若不能建立理想的模糊規則，則很難達到預期的效果。

滑模變結構控制不依賴于水冷壁磨損檢測機器人的精確數學模型，與其他控制方法相比，具有響應迅速，能夠克服系統的不確定性，控制算法簡單，魯棒性好等諸多優點，適合對于在鍋爐內部這樣復雜環境下作業的機器人的控制。本文以磨損檢測機器人運動模型為基礎，根據滑模變結構控制理論設計一種基于指數趨近律的滑模變結構控制器。由于在滑模變結構控制中，抖振是無法避免的且會影響系統的穩定性，因此系統引入“準滑膜動態”，將磨損檢測機器人的運動軌跡限制在一定領域內，采用邊界層法解決抖振問題[7]，再通過Lyapunov穩定理論驗證其穩定性。最后通過MATLAB軟件模擬仿真，仿真結果表明該控制器可以克服誤差，使位姿誤差收斂至零。

1 磨損檢測機器人結構及運動學建模

本文所設計的磨損檢測機器人需要在大型鍋爐內部的水冷壁面上工作，故為了使機器人能夠實現水冷壁的壁厚檢測，磨損檢測機器人的設計需具備以下3個基本要求：

1)牢固可靠地吸附在壁面；

2)能沿水冷壁面進行運動；

3)順利完成水冷壁磨損檢測。

故本文所設計的磨損檢測機器人采用永磁體吸附的吸附方式和履帶式移動的移動方式。永磁體吸附可以保證磨損檢測機器人即使在斷電的情況下也不會發生傾覆的危險。而履帶式的移動方式可確保機器人運行平穩，速度較快。

如圖1所示是磨損檢測機器人的工作環境——水冷壁壁面。鍋爐內的水冷壁主要由鋼制的水冷管相互焊接而成。在鍋爐工作時，其內部會因燃燒而形成高速的飛灰顆粒，從而對水冷壁壁面進行沖刷，造成水冷壁壁面的磨損。故需要對水冷壁進行定期的磨損檢測，防止產生爆管的危險事故。

圖1 水冷壁

1.1 機器人本體結構

本文所設計的水冷壁磨損檢測機器人主要由移動機器人和自動磨損檢測裝置組成，如圖2所示是其三維模型圖。磨損檢測機器人通過裝有特制永磁鐵的履帶吸附在水冷壁壁面，驅動電機通過蝸輪蝸桿減速器帶動鏈輪,鏈輪與鏈條嚙合,從而使機器人沿著水冷管壁運動。

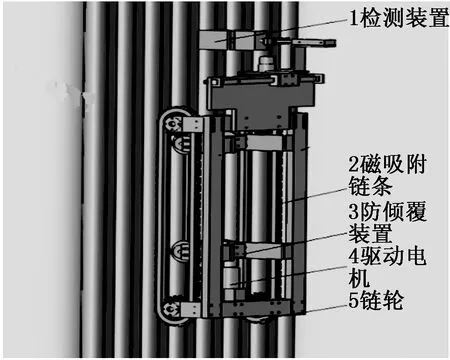
圖2 磨損檢測機器人三維圖

1.2 機器人運動學建模

針對上述磨損檢測機器人，對其進行運動學分析，建立磨損檢測機器人運動模型，掌握其運動規律，為后續控制器的設計奠定基礎。磨損檢測機器人的運動示意圖如圖3所示。

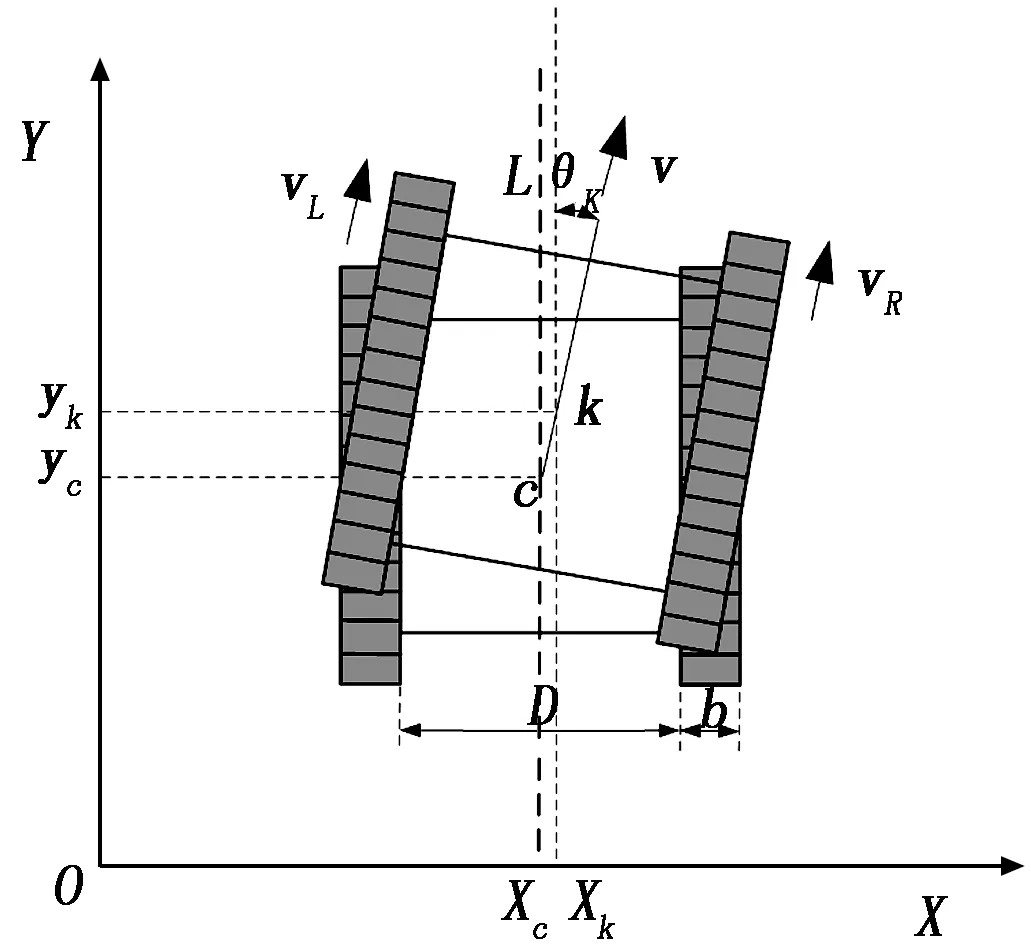
圖3 磨損檢測機器人運動示意圖

水冷壁磨損檢測機器人路徑跟蹤控制器的設計目標是在給定磨損檢測機器人一定速度的前提下，通過計算設計出合適的控制律[vω]，使得在該控制律的作用下，磨損檢測機器人能夠沿著期望的路徑移動。如圖3所示，設在XOY參考平面上，水冷壁磨損檢測機器人以平行于管道L的位姿運動，左右履帶的理論運動速度分別為vL和vR，合成速度為v，磨損檢測機器人的質心運動到C點(xc,yc)，傾斜角度為0°，則磨損檢測機器人的位姿表示為Pc=[xc,yc,0]T，當機器人繼續向前運動，質心運動到K點，機器人的位姿表示為PK=[xK,yK,θK]T。所以水冷壁磨損檢測機器人位姿可由以下公式(1)表示：

(1)

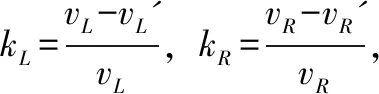
(2)

理想情況下，磨損檢測機器人的偏差角度保持為0°，vL=vR=v，對式(2)求導，可得理想情況下機器人的動力學方程：

(3)

而實際情況下磨損檢測機器人兩側的履帶因制造差異等原因速度不可能完全一致，故機器人將發生傾斜，不妨假設其質心運動到K點時，產生傾斜角度，則可得到在K點時的動力學方程：

(4)

磨損檢測機器人在K點時，其速度為：

(5)

其中，水冷壁磨損檢測機器人的尺寸D=210 mm，d=45 mm。將上式(5)結合式(4)可得機器人的運動方程：

(6)

2 路徑跟蹤運動誤差分析

如圖4所示建立水冷壁磨損檢測機器人運動位姿誤差模型，其中AB為期望路徑。

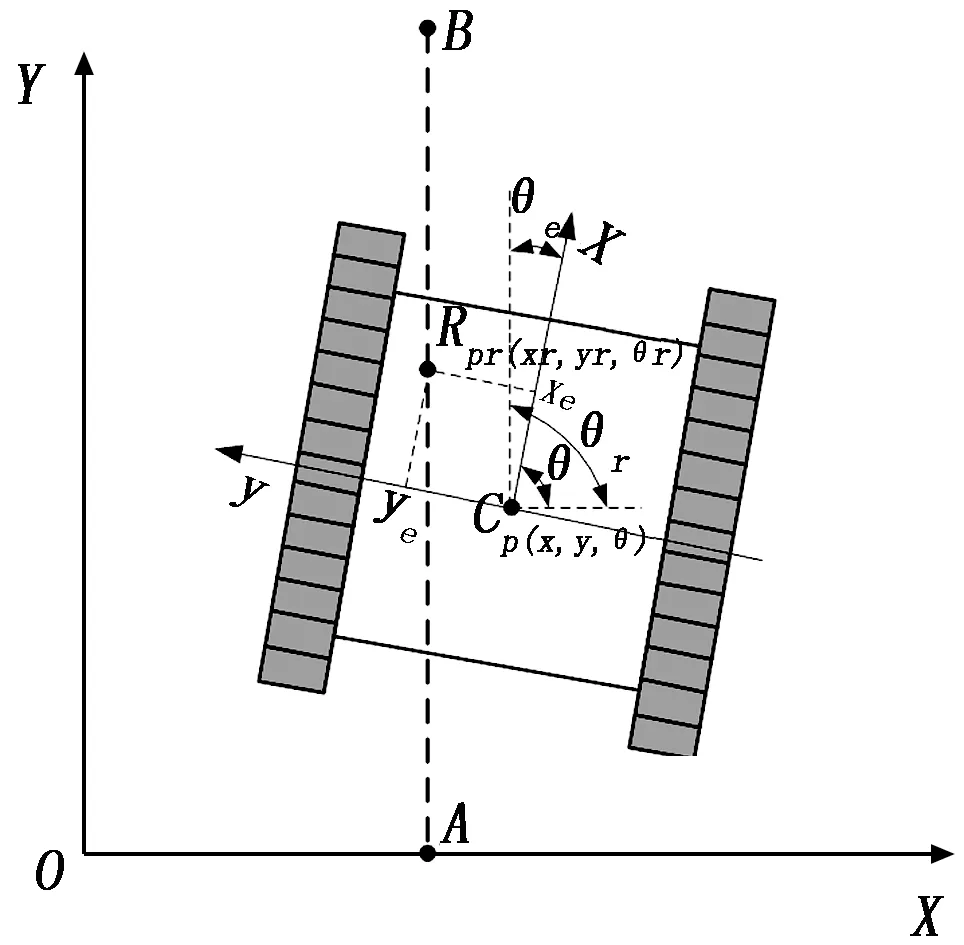
圖4 機器人跟蹤位姿誤差模型

如圖4所示，磨損檢測機器人t=0時，由A開始運動，經時間后，運動到C點，此時機器人位姿可以用表示。在理想情況下，理想機器人從t=0時開始，能夠以期望速度沿期望直線路徑AB運動，之后，到達R點；則在R點的機器人位姿可由表示。

則磨損檢測機器人實際位姿和期望位姿之間的誤差可表示為：

(7)

對上式進行求導，得到機器人位姿誤差微分方程：

(8)

我們期望水冷壁磨損檢測機器人跟蹤期望直線AB運動，所以需要由其實際位姿p=[xyθ]T和期望位姿pr=[xryrθr]T來確定其速度q=[vω]T，再通過式(5)計算得到合適的u=[vLvR]，通過調控運動狀態值u=[vLvR]使局部位姿誤差pe=[xeyeθe]T收斂至零，達到精確跟蹤的目的。

3 滑模變結構控制器設計

滑模變結構控制屬于非線性控制，其非線性是指控制的不連續，并且其“結構”不是固定的，可以依賴偏差進行變化，使系統按照預定的軌跡滑動。與其他傳統控制方法相比，滑模變結構控制具有：響應迅速，能夠克服系統的不確定性，控制算法簡單，魯棒性好等諸多優點[8]。目前，在控制領域得到了廣泛的應用。

滑模變結構控制的本質是一種特殊的非線性控制，而該特性致使系統的狀態被控制在某一子流形上運動，即“滑動模態”運動。滑模運動包括：趨近運動、滑模運動。趨近運動是指系統由某一個初始狀態到達其切換面的運動，而為了提高趨近運動的運動品質，高為炳教授提出了滑動模態趨近律的概念。常用的趨近律有以下4種比較典型的趨近律：

1)等速趨近律:

(9)

其中，常數ε表示趨近切換面的速率，ε較大可以使趨近速度較快，但會引起抖動，sgn(s)表示符號函數。

2)冪次趨近律：

(10)

其中，α較大，可以較快趨近滑動模態，當α較小，可以降低抖振。

3)一般趨近律：

(11)

其中:f(0)=0，當s≠0，sf(s)>0。

4)指數趨近律：

(12)

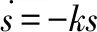
指數趨近律既可以縮短趨近時間，而且到達切換面的速度較小，所以本文選擇指數趨近律來完成控制器的設計。

3.1 基于指數趨近律的控制律設計

水冷壁磨損檢測機器人的路徑跟蹤需要通過控制其輸入狀態q=[vw]T使跟蹤誤差pe=[xeyeθe]T趨向于零。設計滑模切換函數為[9]：

(13)

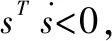
(14)

使α=tan-1(vrye)，帶入公式(8)和式(14)可得:

(15)

由上式(15)變換可得其控制器的控制律為：

(16)

在滑模變結構控制中，需要頻繁地切換系統的控制狀態，而在實際系統中不存在理想的切換，所以對一個實際系統而言，抖振是不可避免，一定存在的。但抖振的存在會影響到系統控制的穩定性，因此本文引入“準滑模動態”，將水冷壁磨損檢測機器人的運動限制在一定鄰域內，采用邊界層法，解決抖振問題。

為解決抖振的問題，使用連續函數?(si)=si/(|si|+δi)代替原來的符號函數sgn(si)，即：

(17)

式(17)中，δ1，δ2為很小的正數。將式(17)帶入(16)，得到新的控制律：

(18)

在上式(18)中，可以通過改變δ1和δ2，從而改變“邊界層”的寬度，其值越小[10]，則誤差收斂的范圍越小。

3.2 穩定性證明

根據引理1[11]：對于任意x(x∈R)且滿足|x|<∞，有φ(x)=xsin(tan-1x)≥0，當且僅當x=0時等號成立。

當xe=0，設計Lyapunov函數：

(19)

設θe=-tan-1(vrye)，可得：

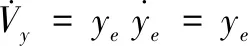
(20)

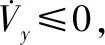
4 跟蹤仿真實驗與分析

在MATLAB平臺上，編寫程序，進行跟蹤實驗，驗證控制器的有效性[12]。假設水冷壁爬壁機器人的實際初始位姿P0=(0.32,0.5,5π/12)，期望初始位姿PA=(0.25,0.1,π/2)，期望終點位姿PB=(0.25,4,π/2)，期望速度vr=0.3 m/s，期望角速度ωr=0。取參數ε1=ε2=0.5，k1=k2=4，δ1=0.1，δ2=0.05。經過多次實驗后，直線路徑跟蹤仿真如圖5所示，位姿誤差如圖6所示。

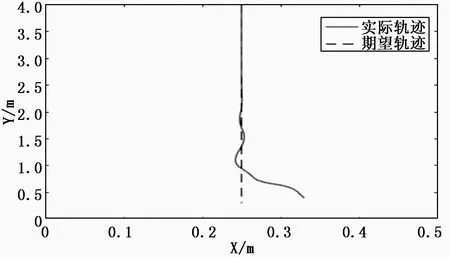
圖5 直線軌跡跟蹤仿真

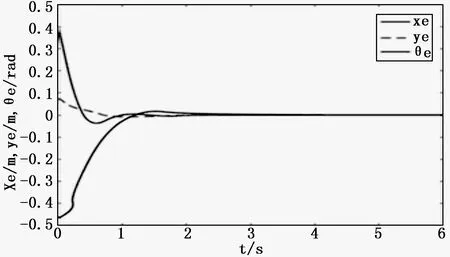
圖6 機器人位姿誤差仿真

由圖5和圖6可知，在基于指數趨近律的滑模變結構控制器的調節下，系統在2s內便達到穩定狀態，位移跟蹤誤差收斂到零，且控制器輸出曲線較為光滑，跟蹤誤差量的超調量較小[13]。

因此滑模變結構控制器可以使水冷壁磨損檢測機器人更加平穩的趨近期望路徑，并且跟蹤直線路徑運動；而誤差、和的超調量較小，變化平穩，且逐漸收斂到零[14]。因此，采用上述設計的滑模變結構控制器可以控制水冷壁磨損檢測機器人沿期望的路徑穩定的爬行，控制器的控制作用穩定可靠[15]。

5 結論

本文針對鍋爐水冷壁磨損檢測機器人的路徑跟蹤問題，提出了一種基于指數趨近律的滑模變結構控制的機器人路徑跟蹤方法，并利用Lyapunov定理驗證其收斂性。最后通過MATLAB軟件模擬仿真，仿真結果表明該控制器可以使水冷壁磨損檢測機器人更加平穩的趨近期望路徑，并跟蹤直線路徑運動；且誤差超調量較小，變化平穩，逐漸收斂至零。該滑模變結構控制器設計可靠，應用性較好。