端面型槽廣義對數螺旋線的通用模型與應用

江錦波 徐奇超 陳 源 趙文靜 彭旭東

浙江工業大學過程裝備及其再制造教育部工程研究中心，杭州，310014

0 引言

以氣體作為潤滑介質的推力軸承和氣膜端面密封具有低摩擦阻力、高精度、污染小和長使用壽命的特點，在高速旋轉機械軸端和高精度加工設備上得到廣泛應用。為保證兩相對運轉端面之間有一層穩定的微米級氣膜，在摩擦副的某一端面上需開設能產生流體動靜壓效應的結構，如動壓淺槽、節流孔或微孔織構等，其中以對數螺旋槽為代表的動壓淺槽結構應用最廣。

對數螺旋槽具有強流體動壓效應和高氣膜穩定性，是干氣密封[1]和氣體推力軸承端面結構的首選端面結構，但目前并沒有明確的分析表明對數螺旋線在任何條件下都是最優的端面型槽型線。近幾十年來，國內外學者一直在探索將其他經典幾何型線作為端面型槽型線的可能性。SALANT等[2]、LIU等[3]對比分析了斜直線槽與螺旋槽的機械密封和推力軸承的泄漏和承載特性，指出型線對端面流場的影響明顯。吳宗祥等[4]、CHEN等[5]、胡丹梅等[6]分別對比分析了直線槽、超橢圓曲線槽和圓弧槽的氣膜密封與螺旋槽氣膜密封的穩動態特性，指出直線槽適用于低速條件。經典的幾何型線具有數學方程明確、模型描述方便等優點，但受限于型線數學模型的固有特性，難以實現端面密封和推力軸承承載特性與氣膜穩定性的進一步提升。

近年來，隨著智能優化算法的發展，國內外學者采用遺傳算法、SQP等方法對端面型槽進行形狀優化，獲得了不同條件下端面型槽的最佳形狀。HASHIMOTO[7]、SHEN等[8]、魏超等[9]以樣條曲線表征型槽型線，采用智能優化算法對氣體推力軸承和液體機械密封的型線進行優化，以期獲得最大的承載力和流體膜剛度；許鵬先等[10]、丁雪興等[11]則以流體流線的擬合曲線為型槽型線，獲得了以5次多項式表達的最佳型槽型線。樣條曲線和多項式的數學模型比較復雜，且不具典型性，構造表征能力更強的型線通用數學模型還有待進一步探索。

在對數螺旋線基礎上，筆者提出了一種幾何表征能力更強的廣義對數螺旋線，并獲得了斜直線、圓弧線、拋物線和橢圓線等經典幾何型線的廣義對數螺旋線表征方程，對比分析了廣義對數螺旋角的分布和變化幅值對廣義對數螺旋槽氣體軸承承載力和氣膜剛度的影響規律。

1 分析模型

1.1 廣義對數螺旋線的通用方程

對數螺旋線的極坐標方程為

r=r0exp(θtanβ)

(1)

式中，r為極徑；r0為起始極徑；β為螺旋角；θ為極徑r處的對數螺旋線與起始點之間的周向夾角。

對數螺旋線的終止極徑為

rn=r0exp(αtanβ)

(2)

式中，α為對數螺旋線起始點與終止點之間的周向夾角，也稱為極角。

定義任一型線在周向角θ處的切線與該點圓周線切線之間所夾的銳角為廣義螺旋角β(θ)。理論上，任一連續光滑的型線都可看成是由無數段首尾相連的對數螺旋線微段組成的，統稱為廣義對數螺旋線。將廣義對數螺旋線作為側壁型線的端面型槽稱為廣義對數螺旋槽，其中，廣義對數螺旋角沿周向恒為定值的對數螺旋槽是廣義對數螺旋槽的一種特例。

后來有些婦女開始說，這是全鎮的羞辱，也是青年的壞榜樣。男子漢不想干涉，但婦女們終于迫使浸禮會牧師—-愛米麗小姐一家人都是屬于圣公會的-—去拜訪她。訪問經過他從未透露，但他再也不愿去第二趟了。下個禮拜天他們又駕著馬車出現在街上，于是第二天牧師夫人就寫信告知愛米麗住在亞拉巴馬的親屬。

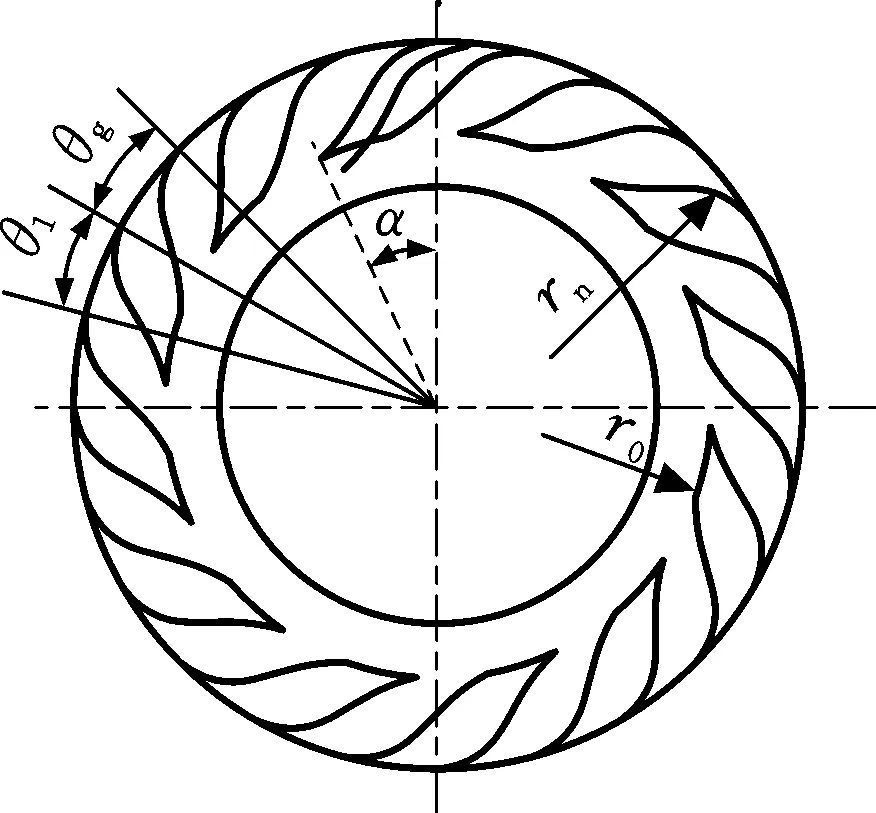
圖1a所示為典型的機械密封或推力軸承端面廣義對數螺旋槽的幾何結構。一個計算周期內，槽區和堰區的周向夾角分別為θg和θl，則槽寬堰寬比δ=θg/θl。圖1b所示為廣義對數螺旋線的幾何結構和參數定義，可將廣義對數螺旋線看成是由n段普通對數螺旋線組成的，則第i段對數螺旋線的極坐標方程為

(3)

(4)

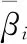
(a) 廣義對數螺旋槽

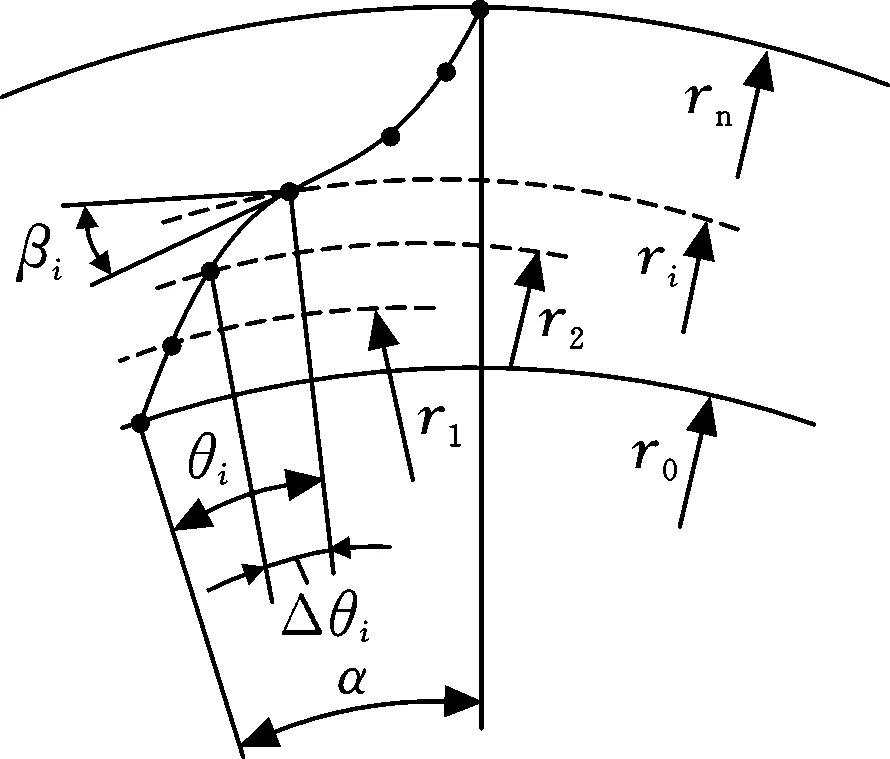
(b) 廣義對數螺旋線圖1 廣義對數螺旋線及廣義螺旋角分布Fig.1 Generalized logarithmic helix and generalized spiral angle distribution

為方便起見，將廣義對數螺旋線看成是由n段周向等角度的普通對數螺旋線組成的，即將廣義對數螺旋線周向n等分，則第i段對數螺旋線的Δθi=α/n。當對數螺旋線微段無窮多時，式(3)寫成積分形式：

(5)

1.2 氣膜承載特性求解模型

氣體推力軸承端面間的流體可假設為層流、等溫的等黏度氣體，則計算軸承端面氣膜壓力的量綱一穩態Reynolds方程為

(6)

式中，p、h分別為端面任意點處的氣膜壓力和膜厚；pi為內徑處壓力；Λ為密封壓縮數；ω為角速度；μ為氣體黏度，下標i表示密封環內徑的參數。

求解式(6)的強制性壓力邊界條件為：在軸承內徑ri和外徑ro處，Pin=Pout=1。周期性邊界條件為P(θ+2π/Ng,R)=P(θ,R)，其中，Ng為密封周期數。

圖2為氣膜壓力分布和穩態性能計算的流程圖，其中，κ、e分別為收斂因子和收斂殘差，本文中取為-0.8和10-6，k為計算次數；下標i、j分別為密封端面周向和徑向節點序號，m、n為密封端面單個計算的周期周向和徑向網格數，本文中均取為150。采用有限差分法按照圖2所示的程序流程求解式(6)，獲得端面壓力分布，進而獲得端面承載力F和軸向氣膜剛度kz：

(7)

(8)

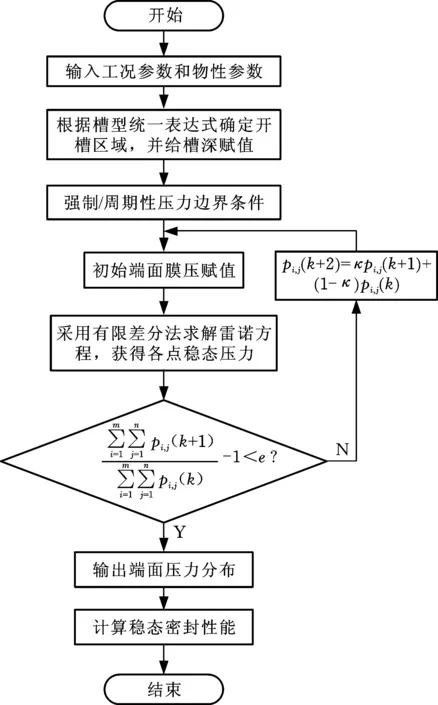
圖2 氣體軸承穩態性能求解流程圖Fig.2 Flow chart of steady-state performance calculation of gas bearing

2 結果分析與討論

不同形狀廣義對數螺旋槽軸承性能對比時，對比基準對于對比結果至關重要，參與對比的不同廣義對數螺旋槽型線的周向角度、周向開槽寬度和徑向開槽寬度等參數相等。本文分析計算時采用的軸承幾何結構參數和操作參數如下：軸承內徑ri=80 mm，槽底半徑rb=90 mm，軸承外徑r0=100 mm，基準對數螺旋槽螺旋角β=15°，初始膜厚h0=3 μm，槽深hg=5 μm，槽寬堰寬比δ=1.0，轉速n=10 000 r/min，軸承外徑側與內徑側壓力都為大氣壓pa=101 kPa。

2.1 經典型線的廣義對數螺旋線形式

直線、圓弧線、拋物線和橢圓線是幾種經典的數學幾何型線，國內外學者探討了將上述經典幾何型線作為機械密封或推力軸承端面型槽側壁型線的可行性，推導了這4種經典幾何型線的廣義螺旋角形式，對比分析了將上述型線作為側壁型線的廣義對數螺旋槽推力軸承的承載特性[4,6]。

表1所示為4種幾何型線的極坐標方程及其對應的廣義螺旋角。圖3所示為直線、圓弧線、拋物線、橢圓線和經典對數螺旋線的幾何模型及對應的廣義螺旋角分布，其中，A點、B點分別為幾何型線的起始點和終止點。從終止半徑rn(外徑側)至起始半徑r0(內徑側)，直線的廣義螺旋角β(θ)呈單調遞減分布，圓弧線的廣義螺旋角β(θ)近似符合線性遞增分布，拋物線的廣義螺旋角β(θ)近似符合拋物線分布，橢圓線的廣義螺旋角β(θ)近似符合對數分布。

表1 經典幾何型線的極坐標方程及其廣義螺旋角Tab.1 Polar coordinate and generalize spiral angle of typical molded lines

(a) 經典幾何曲線

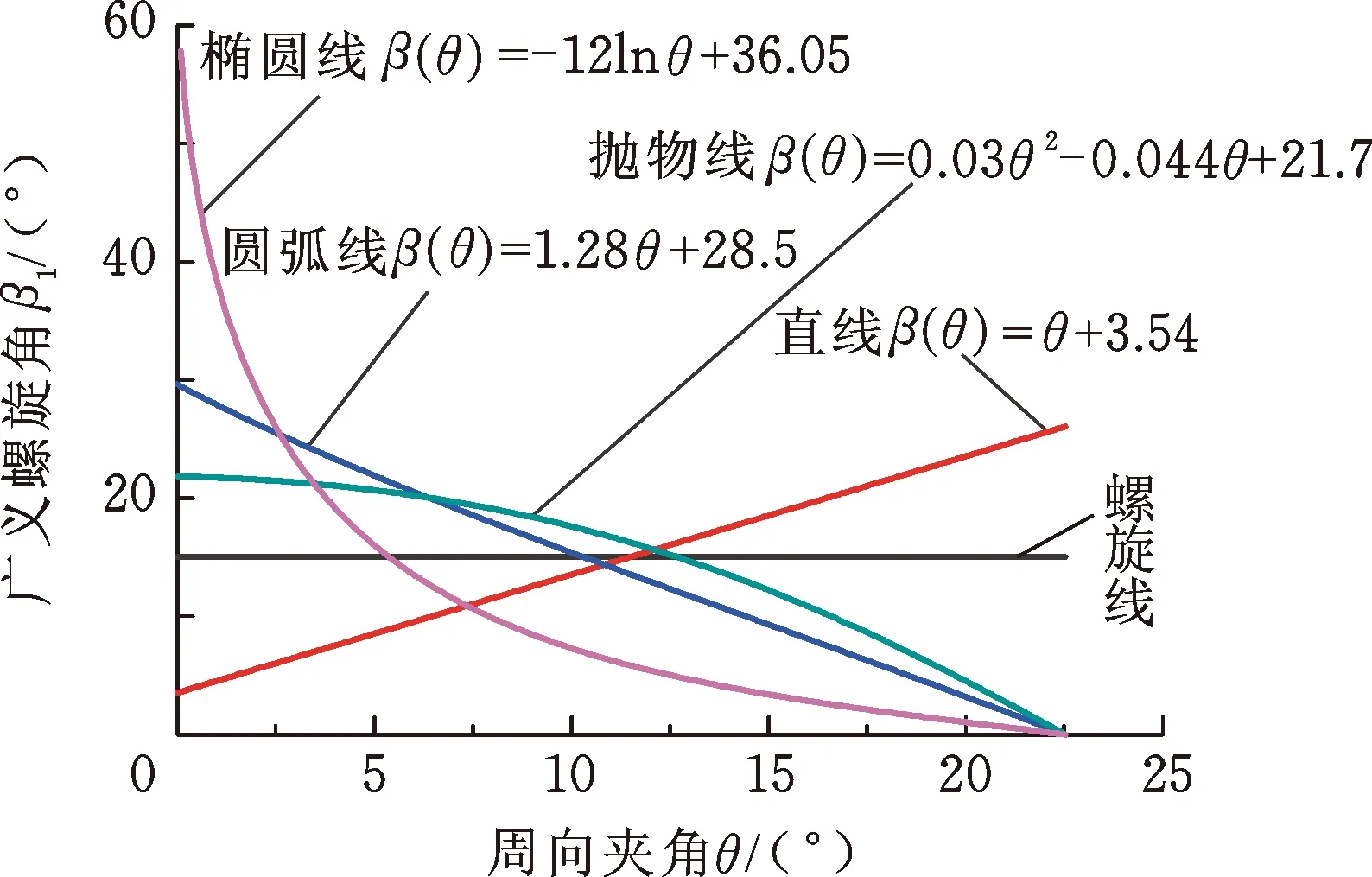
(b) 廣義螺旋角圖3 經典幾何曲線及其廣義螺旋角分布Fig.3 Typical geometrical curves and its corresponding generalized spiral angle distribution

實際上，AB之間存在著無數條可能的圓弧線和拋物線，所有可能的圓弧線和拋物線都介于各自的內外邊界型線之間，其中，內邊界型線定義為槽根處的廣義螺旋角最小時的型線，外邊界型線定義為在外徑處的廣義螺旋角最小時的型線，定義量綱一參數λ為圓弧線和拋物線的型線位置系數，λ為0和1分別對應內外邊界型線。圖4所示為不同型線位置系數條件下的圓弧線和拋物線，可以看出，型線位置系數λ很小時，拋物線和圓弧線近似于直線；隨著型線位置系數的增大，圓弧線和拋物線的特征越趨明顯，與其他型線之間的差別也逐漸增大，故下文中選取λ=1的圓弧線和拋物線作為研究對象。

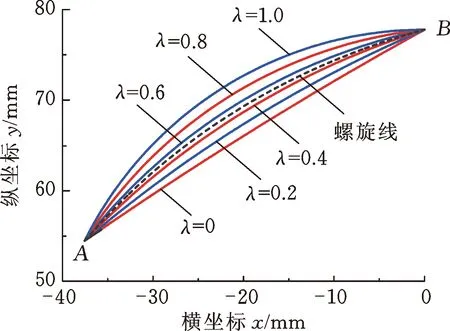
(a) 圓弧線

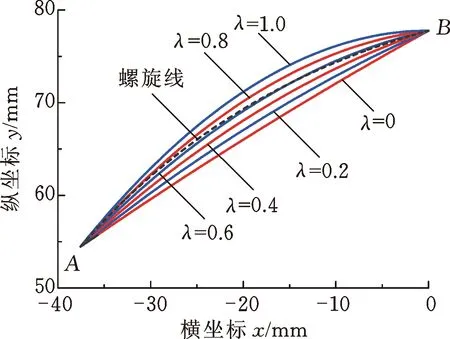
(b) 拋物線圖4 不同參數條件下的圓弧線和拋物線示意圖Fig.4 Schematic diagram of circular arc and parabola at different geometrical parameters

圖5所示為幾種經典幾何型線推力軸承的承載力和氣膜剛度隨轉速n的變化規律。由圖5可知，隨著轉速的增大，承載力和氣膜剛度都減速遞增。高速條件下，經典對數螺旋槽推力軸承的承載力和氣膜剛度最佳，拋物線型槽的次之，圓弧線型槽和橢圓線型槽的最差。這說明經典對數螺旋槽端面具有最佳的流體動壓效應和氣膜穩定性，這與文獻[1]的結論是一致的。實際上，經典幾何型線(圓弧線、直線和橢圓線等)的固有數學模型在方便描述型線的同時，也使得型線的表征能力變差，可優化的尺寸參數減少，將其作為型線的端面型槽往往難以產生很強的流體動靜壓效應。

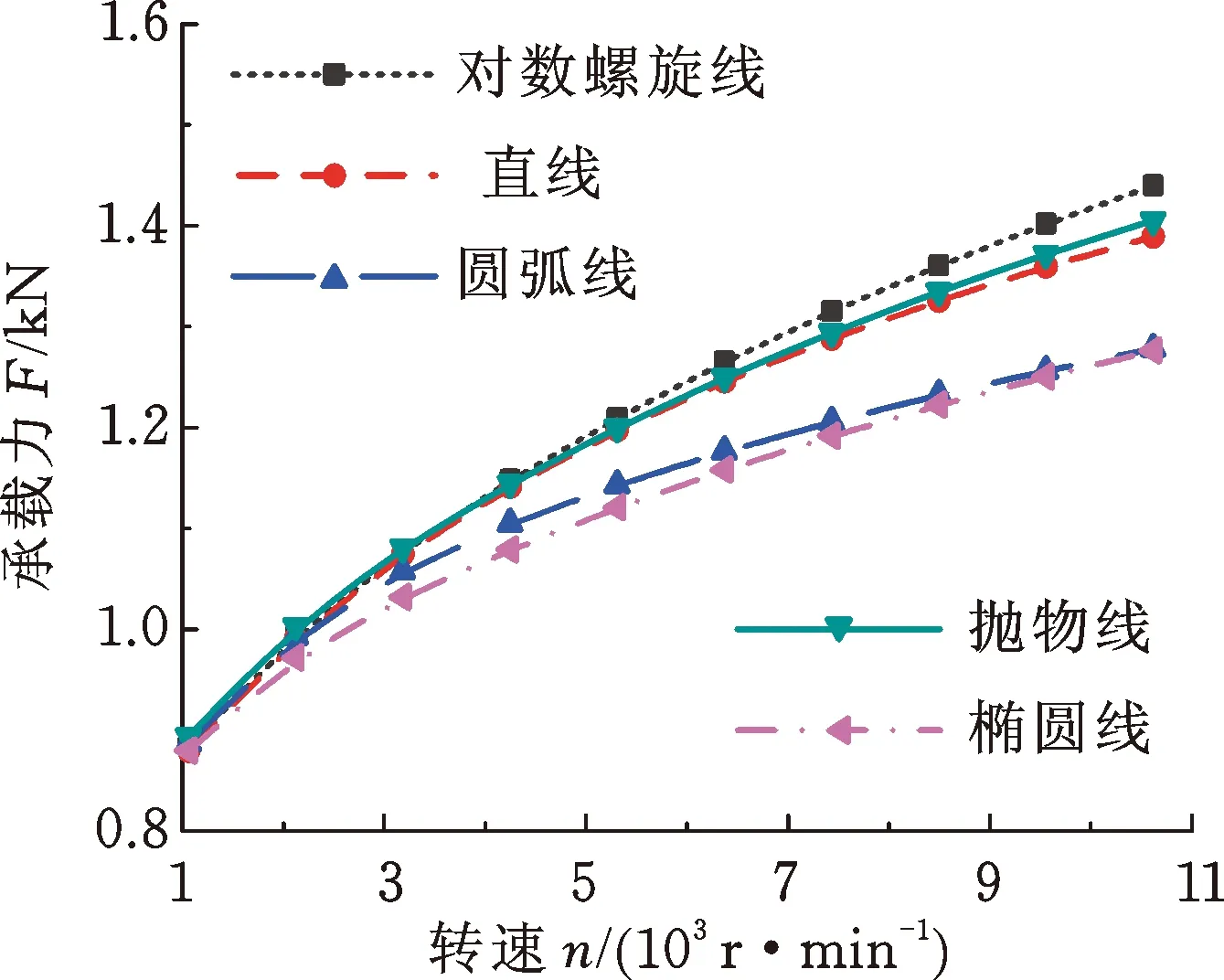
(a) 承載力

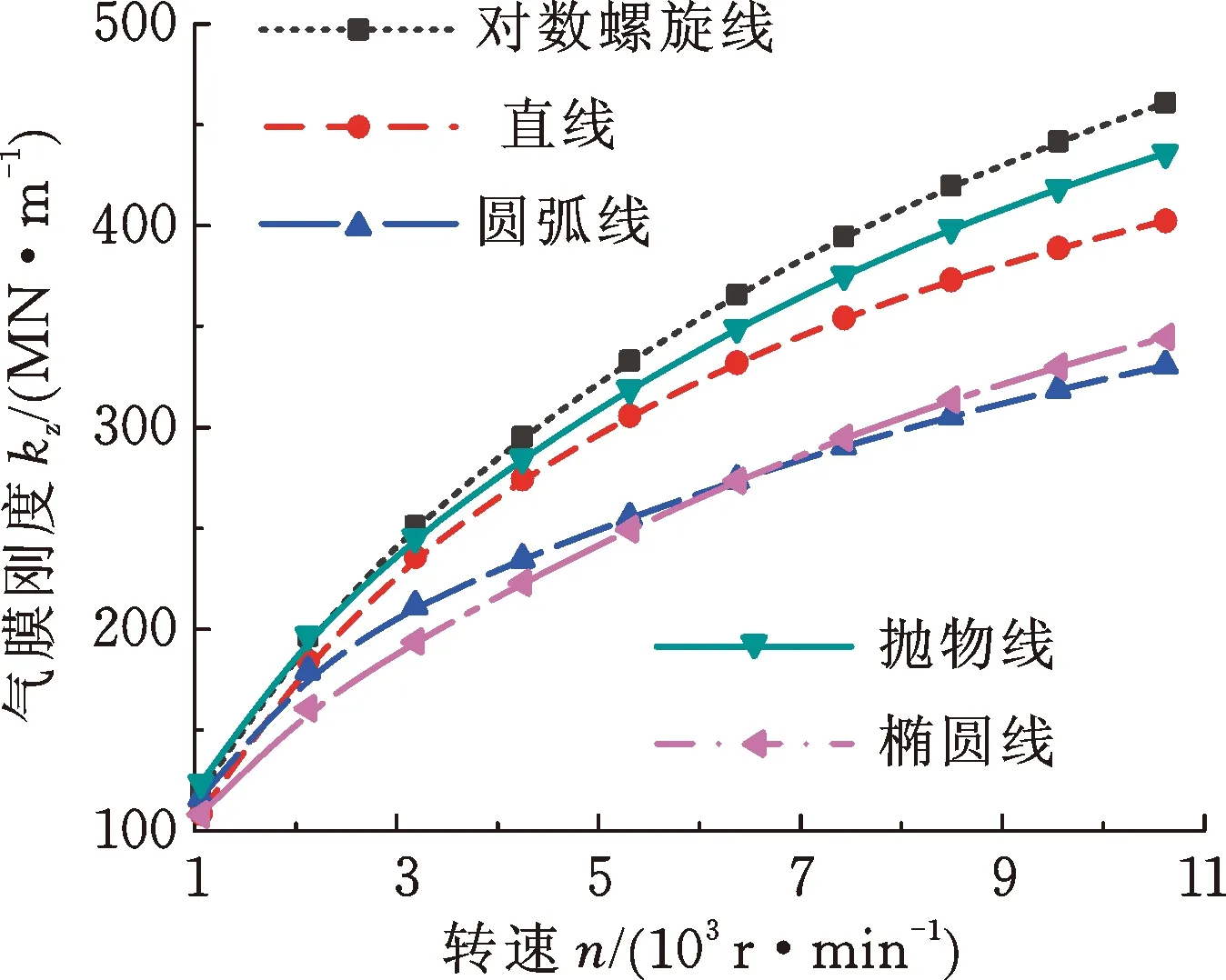
(b) 氣膜剛度圖5 轉速對軸承承載力和氣膜剛度的影響Fig.5 Influence of rotating speed on load-carrying capacity and film stiffness of grooved bearing

2.2 廣義螺旋角分布對軸承性能的影響

從上述經典型線的廣義螺旋角分布可看出，一般型線的廣義螺旋角并非定值，而是沿著周向呈現出一定規律的分布。圖6所示為廣義螺旋角β(θ)沿周向從θn(外徑側)至θ0(內徑側)的變化規律，其中，β1、β2、βav、Δβ分別為廣義螺旋角的最小值、最大值、平均值和變化幅值，θ0、θn、θav分別為廣義對數螺旋線的起始點、終止點和周向等分點的周向角度，圖1b所示的廣義對數螺旋線中，起始角度θ0=0，終止角度θn=α。

β(θ)=aθ+b時，式(5)可寫成：

(9)

表2所示為4種典型β(θ)分布的系數a和b，其中，γ=εβav/(θ0-θn)。

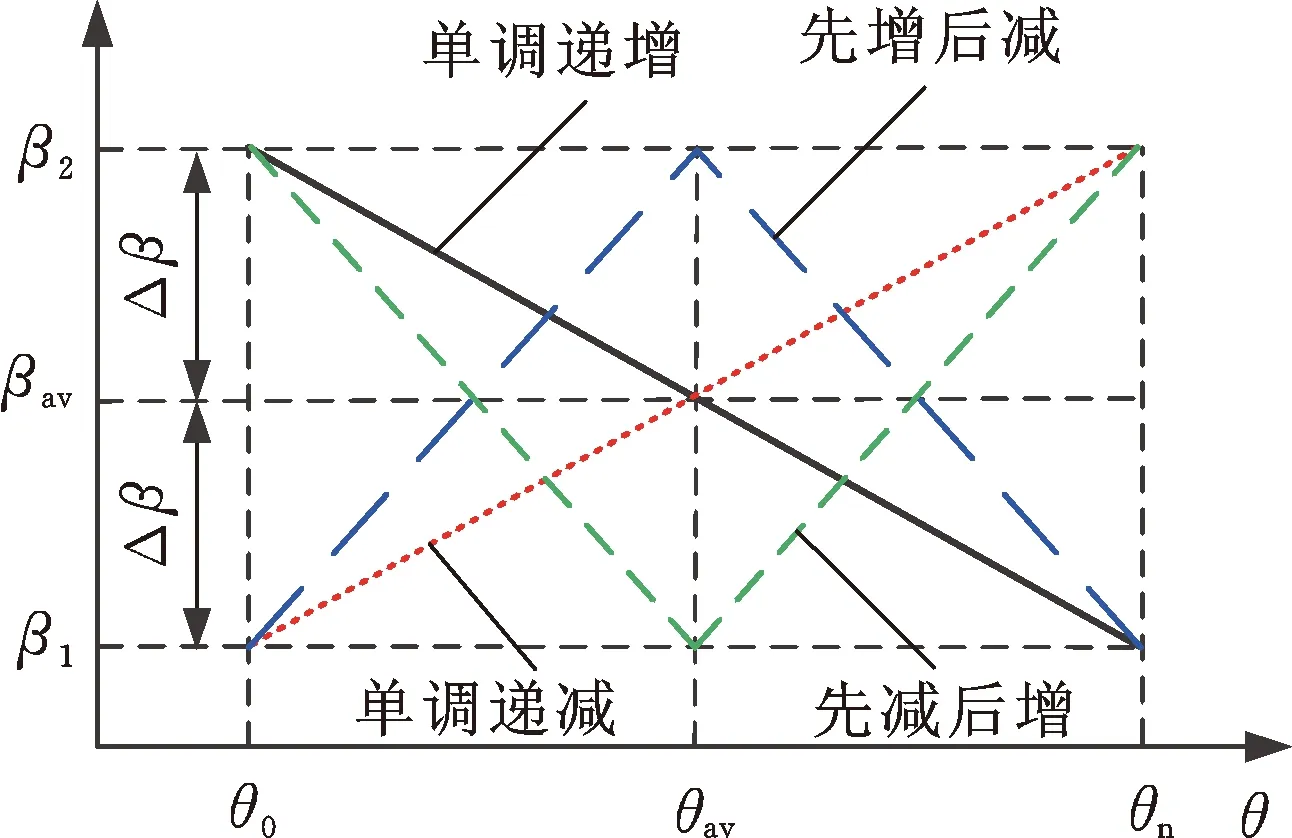
(a)線性分布規律

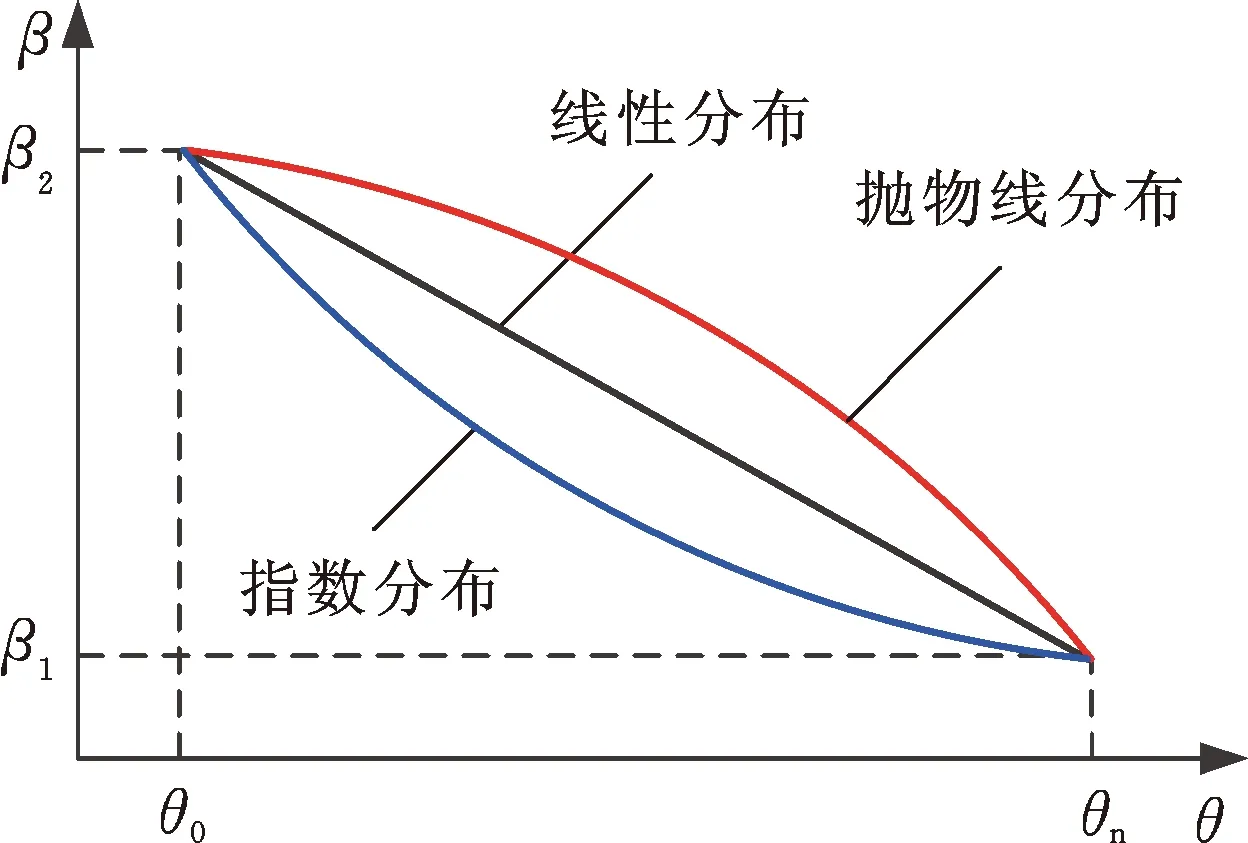
(b)不同分布規律圖6 典型廣義對數螺旋線的廣義螺旋角分布Fig.6 Generalized spiral angle distribution of typical generalized logarithm helix

表2 典型β(θ)分布對應的系數a和b Tab.2 Coefficients a and b for typical distribution of β(θ)

圖7所示為螺旋角變化幅值比ε不同時， 4種典型β(θ)分布的廣義對數螺旋線及其對應的廣義對數螺旋槽。從外徑至內徑側，廣義螺旋角單調遞增時，廣義對數螺旋線對應的型槽流道逐漸變寬，由其作為側壁型線的廣義對數螺旋槽為“流道漸擴槽”(圖7a)；廣義螺旋角單調遞減時，廣義對數螺旋線對應的型槽流道逐漸變窄，由其作為側壁型線的廣義對數螺旋槽為“流道漸縮槽”(圖7b)；當廣義螺旋角先減后增和先增后減時，由其作為側壁型線的廣義對數螺旋槽分別為“先縮后擴槽”(圖7c)和“先擴后縮槽”(圖7d)。螺旋角變化幅值比ε越大，廣義對數螺旋線偏離經典對數螺旋線越遠。由此可見，相較于直線、圓弧線和拋物線等經典幾何型線，廣義對數螺旋線具有更強的型線表征能力，通過改變螺旋角變化幅值比ε和平均廣義螺旋角βav，可實現廣義對數螺旋線向其他經典幾何型線的轉變。

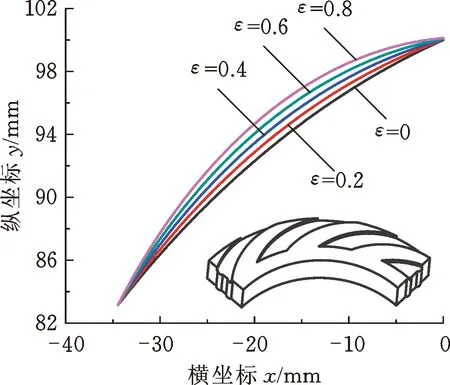
(a) 單調遞增

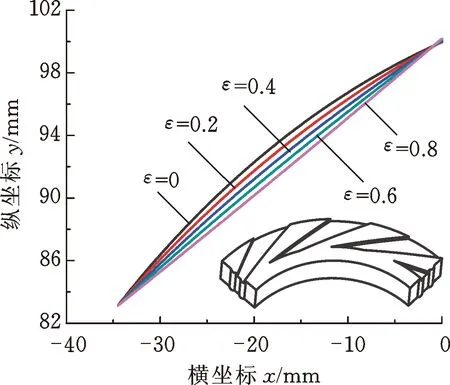
(b) 單調遞減

(c) 先減后增

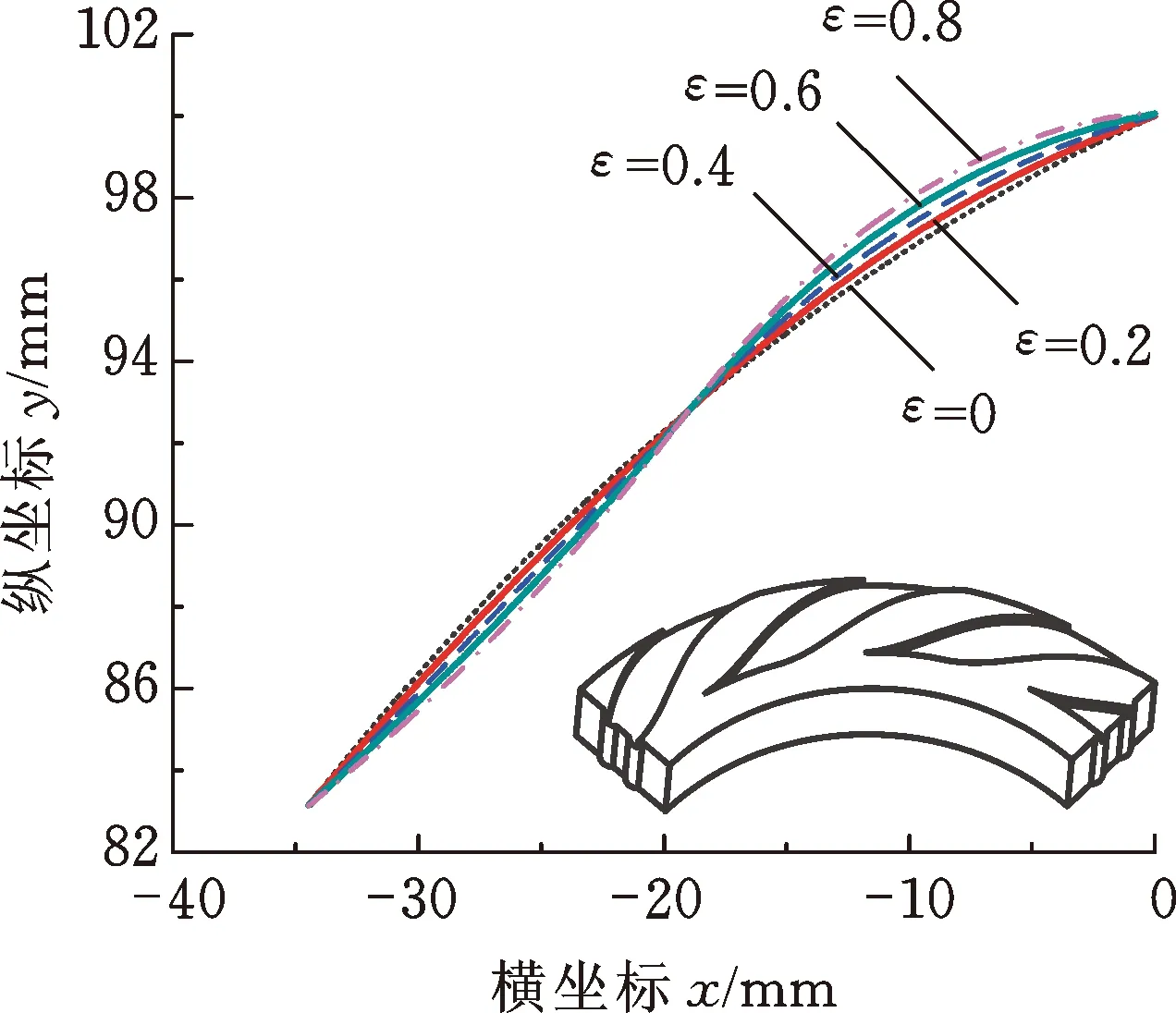
(d) 先增后減圖7 不同ε的4種典型廣義對數螺旋線Fig.7 4 typical generalized logarithm helixes at different ε

圖8所示為4種典型螺旋角分布的廣義對數螺旋槽推力軸承的承載力和氣膜剛度隨幅值比ε的變化規律，其中，ε=0對應經典對數螺旋槽。由圖8可知，隨ε的增大，流道漸擴槽(β(θ)單調遞增)和先縮后擴槽(β(θ)先減后增)推力軸承的承載力和氣膜剛度都先小幅增加、后迅速減小；流道漸縮槽(β(θ)單調遞減)和先擴后縮槽(β(θ)先增后減)推力軸承的承載力和氣膜剛度都迅速下降。從承載力來看，β(θ)沿周向非定值的廣義對數螺旋槽與經典對數螺旋槽相比，并無明顯優勢；從氣膜剛度來看，0.2≤ε≤0.4時的流道漸擴槽推力軸承相較于經典對數螺旋槽略有提高。

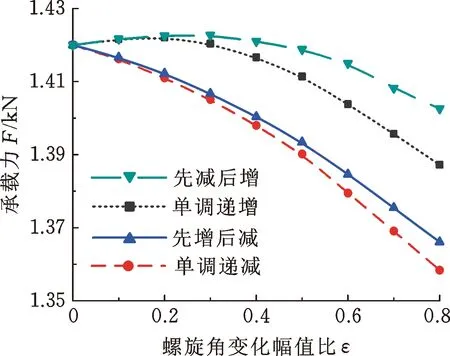
(a) 承載力

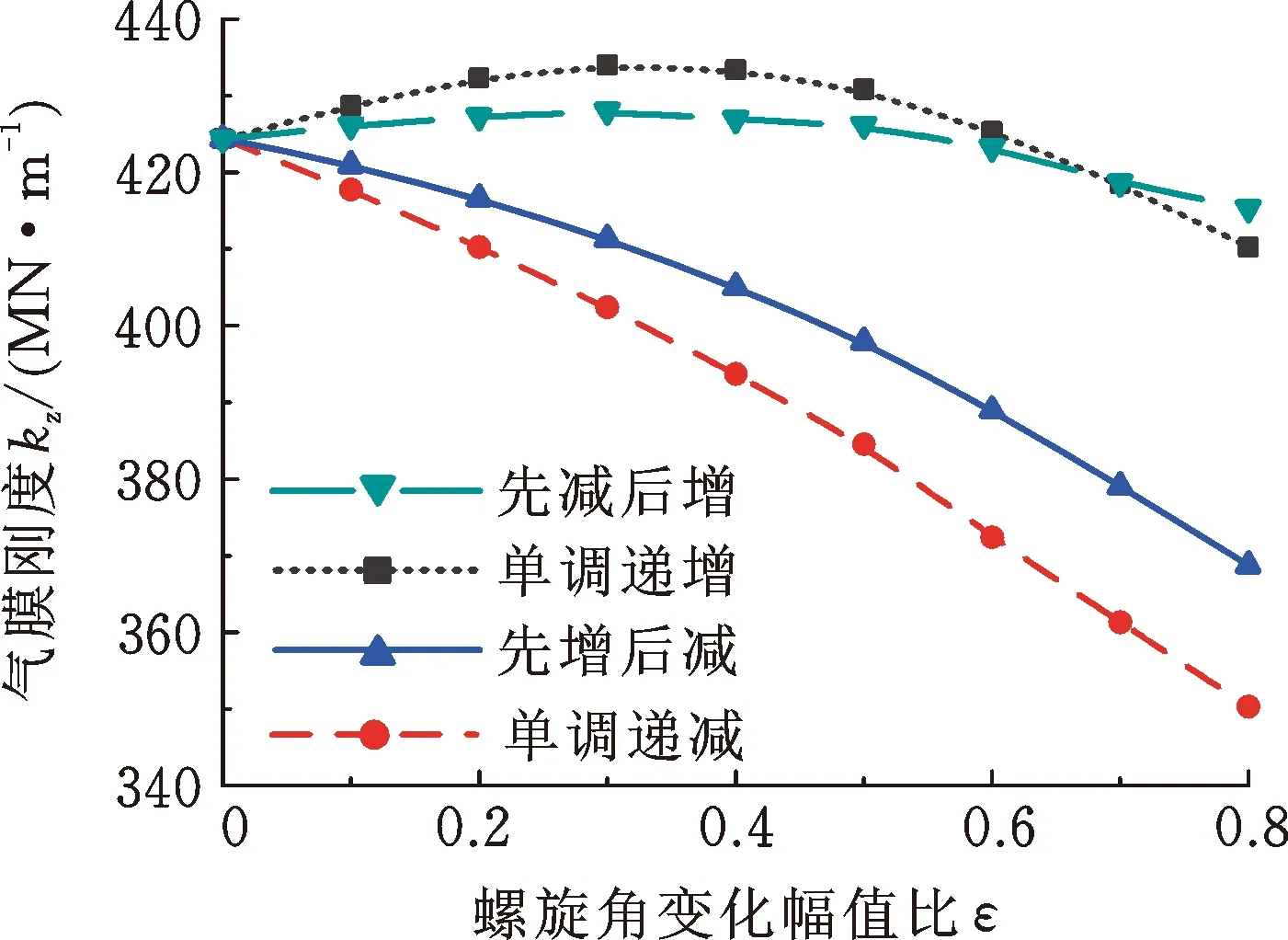
(b) 氣膜剛度圖8 不同ε下螺旋角分布規律對承載力和剛度的影響Fig.8 Influence of spiral angle distribution on load-carrying capacity and film stiffness at different values of ε

為進一步研究β(θ)為單調遞增分布(流道漸擴槽)時，β(θ)對廣義對數螺旋槽推力軸承性能的影響，對比分析了β(θ)分別為線性分布、拋物線分布和指數分布的廣義對數螺旋槽與經典對數螺旋槽推力軸承的承載力和氣膜剛度。由圖9可看出，在靠近外徑側區域，3種不同β(θ)分布的廣義對數螺旋線基本重合；在靠近起始半徑處，指數分布的廣義對數螺旋線在相同周向角度下的極徑最大，線性分布次之，拋物線分布最小。

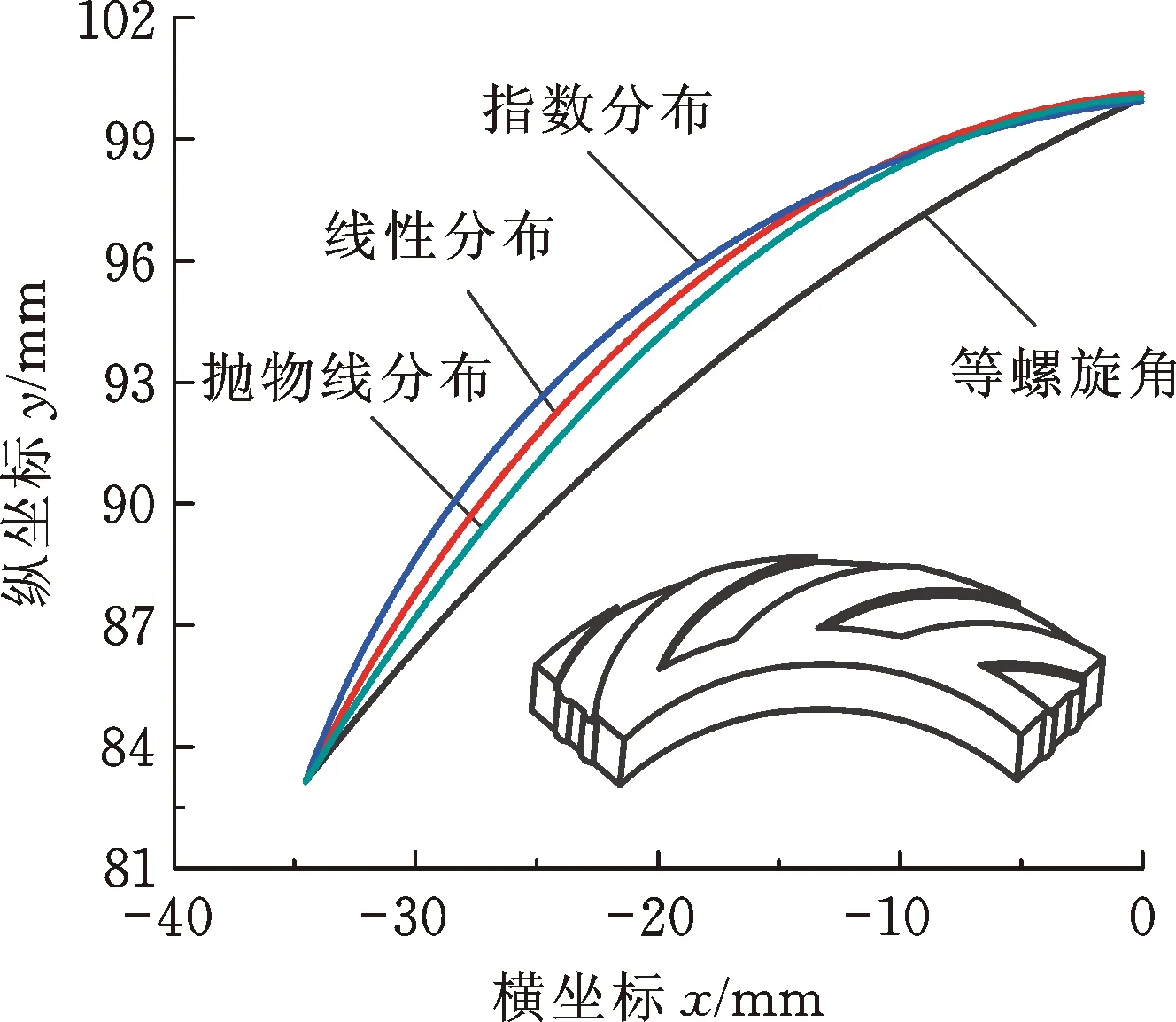
圖9 典型螺旋角分布的廣義對數螺旋線Fig.9 Generalized logarithm helix with typical spiral angle distribution

圖10所示為3種不同β(θ)分布下，廣義對數螺旋槽推力軸承的承載力和氣膜剛度隨ε的變化規律。由圖10可知，隨著ε的增大，廣義對數螺旋槽推力軸承的氣膜剛度呈現出先增大、后減小的變化趨勢，0.2≤ε≤0.5時獲得最大值，不過增幅很小，這也說明廣義螺旋角沿周向的遞增或遞減趨勢一旦確定后，具體的變化規律(線性變化、拋物線變化抑或指數變化)對氣體推力軸承的穩態性能影響較弱。指數分布的廣義對數螺旋槽推力軸承氣膜剛度最大，線性分布次之，拋物線分布最小。這是因為在高速條件下，周向剪切流占主導作用。β(θ)呈指數分布時，廣義對數螺旋槽入口處較小的螺旋角有利于將密封腔內的氣體介質泵入到密封端面之間，產生更強的流體動壓效應。

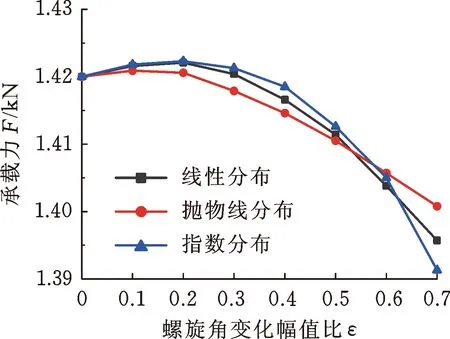
(a) 承載力

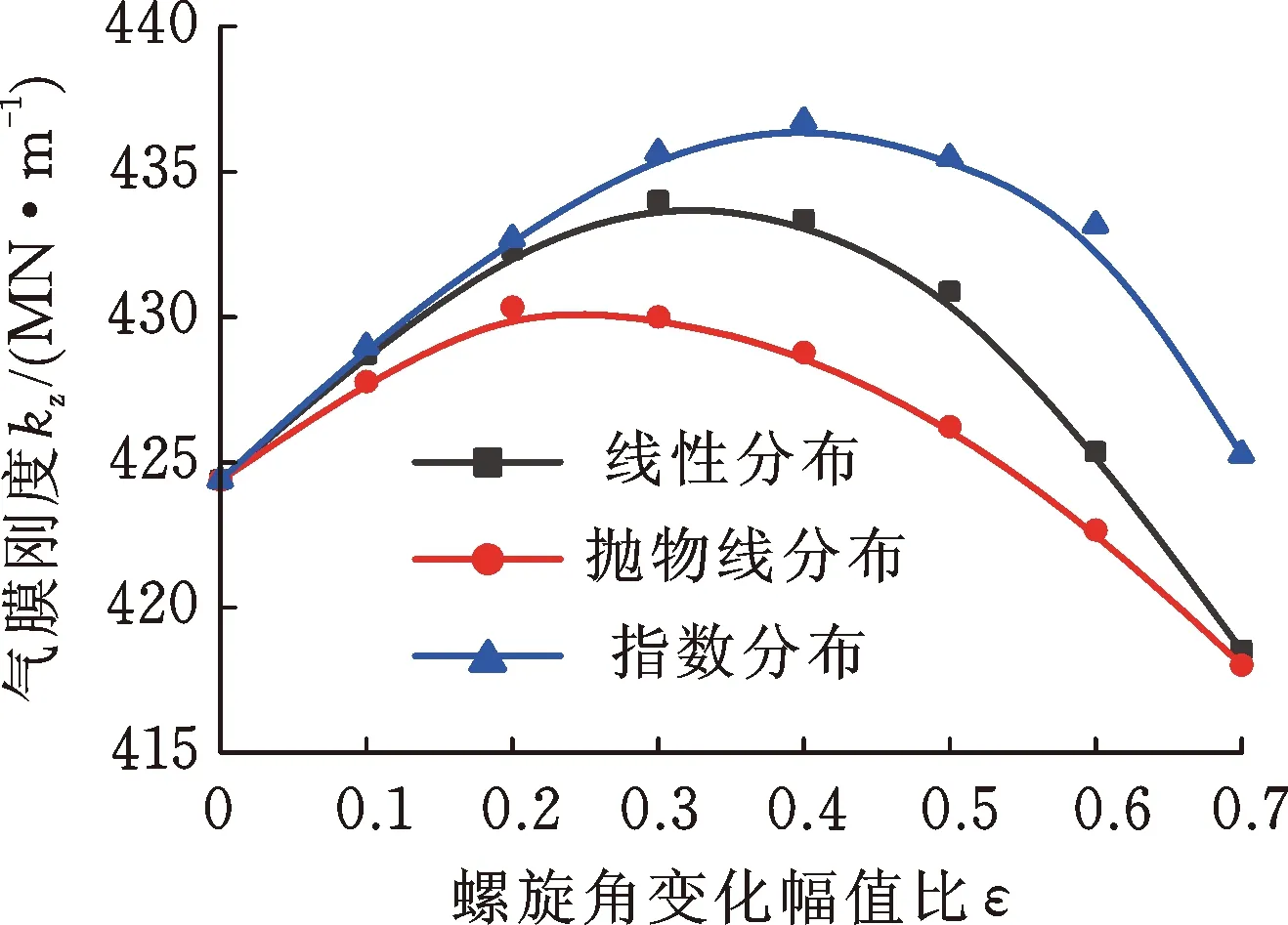
(b) 氣膜剛度圖10 β(θ)分布規律對推力軸承承載力和氣膜剛度的影響Fig.10 Influence of β(θ) distribution on load-carrying capacity and film stiffness of thrust bearings

3 結論

(1)針對經典幾何型線受其固定數學模型固有特性的限制，基于對數螺旋線方程，推導出廣義對數螺旋線的極坐標方程，它相較于經典的直線、圓弧線、拋物線和橢圓線具有更強的幾何表征能力。

(2)經典對數螺旋槽推力軸承的承載力和氣膜剛度都優于將直線、圓弧線、橢圓線和拋物線作為側壁型線的廣義對數螺旋槽推力軸承，對數螺旋槽是一種能產生較強流體動壓效應的端面結構。

(3)在高速條件下，相較于對數螺旋槽推力軸承，從外徑至內徑型槽流道漸擴的廣義對數螺旋槽推力軸承具有更大的氣膜剛度，其中，以廣義螺旋角呈指數遞增分布為最佳。