從手工研磨咖啡的決策來談人工智能教學中的取舍

陳凱

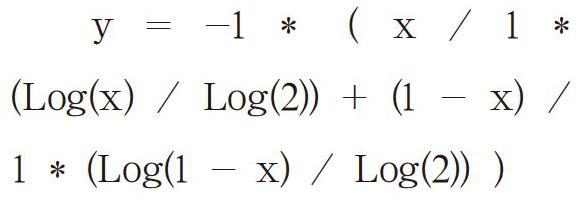
小馨同學每天早晨上學和傍晚放學時，都要到街邊的醇香咖啡屋里坐上那么一會兒，她有時會點上一杯手工研磨的咖啡，有時候喝橙汁。

小嚴同學正在做一份關于飲用咖啡習慣的社會調查，小馨同學是他的研究對象。

小嚴同學統計后發現，小馨同學走進咖啡屋六次，有三次喝了咖啡，還有三次沒有喝。（對于真正的科學統計來說，這點樣本數顯然太少了，本文的重點不在于統計學，所以只取了非常少的所謂樣本）這個數據最多說明，小馨同學喝咖啡的比例是否為五比五，除此之外似乎沒有其他什么用處。然而，小嚴是個細心的同學，他注意到，那是一家奇怪的咖啡屋，它提供的咖啡，要么是甜咖啡，要么就是清咖啡，在某一時刻，兩種口味中只有一種;還有，它提供的要么是熱咖啡，要么是冰咖啡，在某一時刻，兩種溫度中只有一種。經過記錄后，小嚴同學所觀察到的小馨同學的行為是這樣的：

溫度? 味道? 時間? 是否喝咖啡

熱? ?甜? ? 早? ?喝

熱? ?甜? ? 晚? ?不喝

熱? ?淡? ? 早? ?喝

熱? ?淡? ? 晚? ?不喝

冰? ?甜? ? 晚? ?不喝

冰? ?淡? ? 早? ?喝

看了這樣一份記錄表，小嚴同學心中產生出一個疑問：如果小馨同學晚上走進咖啡屋，那里只提供冰的淡咖啡，那么她更有可能喝咖啡，還是不喝？畢竟，冰、淡、晚這三個屬性的組合，在已有的記錄表中并沒有出現過。

這篇文章中的例子，是要從信息熵的角度，來說明機器將如何根據已有的數據，對未來的行為做出預測;同時，通過這個例子，我們可以討論在基礎教育階段，在人工智能教學過程中某些環節所涉及的知識和技能超出學生當前水平的情況下，應該如何做出取舍。

● 事件概率均等時的信息熵計算

人工智能教學中的許多內容，是和信息技術教學基礎（必修）模塊中的內容緊密聯系在一起的，人工智能中常見的分類問題的實施過程，其實也正是從混亂走向秩序的過程。信息技術教學中一般都會提到信息論中信息的概念，認為信息是用來消除（隨機）不確定性的東西，這里的“消除”，更多指的是機器按特定算法所做的不確定性的消除，而不是直接以人力消除。隨機不確定性的程度能夠用以比特為單位的信息熵來描述。

然而，在基礎教育階段，不確定性被“消除”的實際工作過程，往往在教學過程中被忽略了。比如，通過計算信息增益來實施分類，是以決策樹的方法實現分類的理論基礎，但在信息技術教學的基礎模塊部分，當提及信息概念時，并沒有再進一步提及信息增益相關內容，于是，就錯失了通向人工智能中決策樹分類問題的一個重要的引導性內容。何以如此？筆者猜測，恐怕是因為信息論中的數學公式的推導和計算會對學生的理解造成比較大的困難。但經過研究和實際教學驗證，筆者發現，還是存在可行的教學方案，在人工智能教學中回避較為艱深的數學公式的推導和計算過程，而將重點放在不確定性消除過程中數學公式的應用上。

考慮小馨喝咖啡的例子，假設未來的事件只有兩類，即“喝”與“不喝”，如果小馨總是選擇“喝”，那么就根本不存在不確定性，則信息熵為0，如果小馨總是選擇“不喝”，信息熵同樣為0。假如“喝”與“不喝”的決策是一半對一半，則信息熵是1（至少需要一位二進制數字來存儲兩類不同的決定）。考慮一下，若小馨的選擇有四種情況，即“不喝”“喝一杯”“喝兩杯”“喝三杯”，則信息熵是2（至少需要兩位二進制數字來存儲四類不同的決定）。如果可選擇的類別是N，而以比特為單位的信息熵是X，則2的X次方等于N，換成對數公式就是X=log2N。這是整個教學過程中很關鍵（也可能是唯一）的數學公式，這個公式也是高中數學中會學習到的內容，學生理解起來難度并不大。

如圖1所示，將小馨是否喝咖啡的兩選一決策與信息熵的關系標注到坐標上，可發現三處特別的位置。三個坐標點處在非零即一的整數位上，然而這就引出了一個新的問題：如果兩類決定出現概率不均等，那么應該如何計算信息熵呢？直觀上就可以猜測出，經過三個整數點的函數圖形最可能是一條弧線，并且函數圖形必然與對數函數密切相關。

● 事件概率不均等時的信息熵計算

就算是只考慮“喝”與“不喝”兩類決定，但若是這兩類決定出現概率不均等，那么應該如何計算信息熵呢？在這里，混雜了概率計算的信息熵公式必然會成為教學過程中較難逾越的深塹。但要記住的是，在信息技術教學中，數學公式是應用工具，在分析不確定性的消除的整個過程中，這個工具很好地展現了運算的結果，而公式本身的推導和計算過程并不是教學重點。

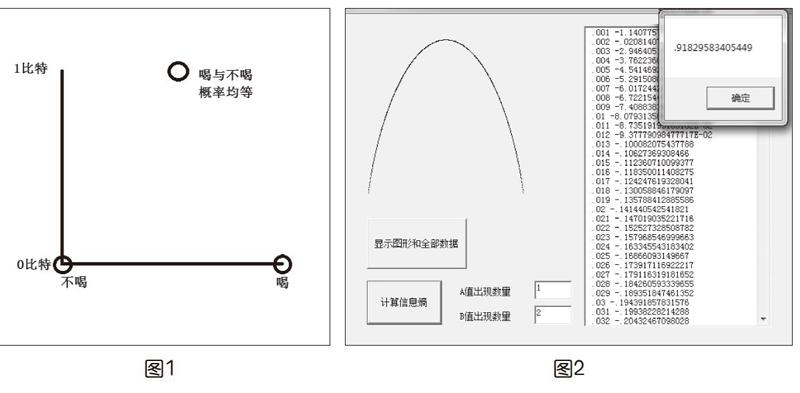
筆者制作了一個簡單的小程序，對于小馨喝咖啡的行為，只要將“喝”與“不喝”兩類選擇各自的次數輸入到程序中（為了使教學過程簡潔明了，這里只考慮兩類決策，而不考慮更多類決策的情況），即可得到該情況所對應的信息熵的值。學生還可以用二分類的信息熵圖表，直觀地感受到信息熵的變化規律，如圖2所示。

實現繪圖的關鍵公式是：

y = -1 * （ x / 1 * （Log（x） / Log（2）） + （1 - x） / 1 * （Log（1 - x） / Log（2）） ）

當X取值為1/2的時候（即兩類不同決定概率均等），則計算結果為1;公式不能將X取值為0或1，但可以無限接近0或1。

在教學中，可告知學生計算結果由此公式而來，但公式的推導過程，則是數學課的任務了。學生在后續的學習過程中，可以直接調用公式，或者使用內置公式的小程序來進行計算。

● 手工決策過程

回到一開始的問題：如果小馨同學晚上走進咖啡屋，那里只提供冰的淡咖啡，那么她更有可能喝咖啡，還是不喝？這個問題并沒有一定的答案，因為小馨的行為完全是自由的。問題的關鍵是，機器應該以什么樣的方式去做出一個合理的預測。如果從信息熵的角度出發，這個問題就轉換為：當以哪一個屬性作為分類依據時，可以使得不確定性（信息熵）減少的程度最大？這個問題便和信息增益有關。

若以溫度作為分類依據，那么可列表如下：

溫度? 是否喝咖啡

1）

熱? ? 喝

熱? ? 喝

熱? ? 不喝

熱? ? 不喝

2）

冰? ? 不喝

冰? ? 喝

供應熱咖啡時，不同決定的比例是對半開，選擇冰咖啡時，不同決定的比例還是對半開，即便不進行計算，也可以直觀地知道，信息熵沒有減少。

若以味道作為分類依據，那么可列表如下：

味道? 是否喝咖啡

1）

甜? ? 喝

甜? ? 不喝

甜? ? 不喝

2）

淡? ? 喝

淡? ? 不喝

淡? ? 喝

無論是對甜咖啡還是淡咖啡，不同決定的比例都是1比2，或2比1，這兩種情況，計算出的信息熵結果都是0.918，這個數字可直接查閱二分類信息熵圖表或二分類信息熵小程序獲得。

若以時間為分類依據，那么可列表如下：

時間? 是否喝咖啡

1）

早? ? 喝

早? ? 喝

早? ? 喝

2）

晚? ? 不喝

晚? ? 不喝

晚? ? 不喝

早上的決定完全一致，晚上的決定也完全一致，則說明信息熵為0。到這里，即便不查表就已經很清楚了，是否喝咖啡，時間可能是最重要的決策依據。機器便可以此為依據，做出判斷，認為小馨不會在晚上喝冰的淡咖啡。

本文提供的數據很簡單，沒有考慮到采樣不平衡的情況，比如，小嚴同學更多是在早上做記錄，而比較少在晚上做記錄;或者咖啡店更多提供的是熱咖啡，而較少提供冰咖啡。使用加權平均，就可以方便地解決此問題，如對于以下記錄數據：

時間? 是否喝咖啡

1）

早? ? 喝

早? ? 喝

早? ? 喝

早? ? 不喝

2）

晚? ? 喝

晚? ? 不喝

晚? ? 不喝

信息熵的計算公式就是：4/7*（1比3情況的信息熵）+3/7*（1比2情況的信息熵）;查對二分類信息熵圖表可知信息熵為：4/7*0.918+3/7*0.811。這一部分工作可由學生親自手工進行，一方面由此了解到機器根據信息熵的計算而進行分類的過程，另一方面也可讓學生在學習過程中增加參與感。

關于小馨喝咖啡的例子分析到這里時，信息增益和決策樹的概念已經呼之欲出了，人工智能教學中的許多內容和信息技術教學基礎模塊中的內容，是有著緊密的聯系的。在基礎模塊的教學中，部分內容只要再稍微深入一點，就可以和人工智能的教學內容無縫對接。筆者認為，在課時及學生知識技能水平有限的情況下，教師在進行人工智能教學時，優先選擇的教學內容應該具有這樣的特點：在教學過程中涉及的知識和技能，最好在信息技術教學基礎模塊或算法模塊中已有所鋪墊;在通向某個具體人工智能教學目標的過程中，能夠找出一條任務需求明確、進階平緩、邏輯清晰連貫的路徑;在教學過程中，既要能回避艱深的數學推導證明過程，又要能彰顯出數學工具在解決問題中的作用。