基于穩健特征點的平穩小波域數字水印算法

牛盼盼，楊思宇，王麗，楊紅穎，李麗，王向陽

（1.遼寧師范大學計算機與信息技術學院，遼寧 大連 116029；2.大連理工大學電子信息與電氣工程學部，遼寧 大連 116023）

1 引言

數字水印是一種可以在開放的網絡環境下保護版權和認證來源及完整性的新技術，目前已成為網絡與信息安全領域的一個研究熱點。不可感知性、穩健性及水印容量是數字水印系統必須滿足的基本要求，也是近年來數字水印領域的主要研究內容[1]。用于版權保護的數字水印系統必須具有高度穩健性。現有大多數穩健音頻水印算法能夠抵抗簡單的常規音頻信號處理攻擊（如疊加噪聲、重新量化、重新采樣、MP3壓縮等），尚無法有效抵抗破壞性較強的去同步攻擊（desynchronization attack）[2-3]。去同步攻擊能夠改變水印信號嵌入位置，即破壞水印信號分量的同步性，使水印檢測器找不到有效的水印信號[4]。數字音頻水印系統中的去同步攻擊可以分為2類：簡單的全局去同步攻擊和復雜的局部去同步攻擊。其中，全局去同步攻擊是針對整段音頻信號的攻擊方式，如時間縮放、幅度伸縮、音調伸縮、DA/AD 轉換等，即對音頻整體內容進行了破壞；局部去同步攻擊是針對局部音頻信號的攻擊方式，如隨機剪切、局部變調、抖動攻擊等，即對音頻信號的一部分內容進行了破壞[5]。

到目前為止，人們主要采納5種策略解決數字音頻水印領域的去同步攻擊問題，包括窮舉搜索、構造同步不變特征、擴頻水印擴頻碼相結合、同步碼、利用音頻重要特征等。

1)基于窮舉搜索的穩健音頻水印

窮舉搜索是數字音頻信號遭受時域去同步攻擊后恢復水印信息的最簡單方法[6]。該類水印算法存在2個致命問題，一是對數字水印檢測器的多次操作會顯著增加虛警率；二是計算復雜度太高，其計算量將隨著搜索空間的擴大而迅速膨脹。因此該類方法只適用于小數據量水印檢測，且無法有效抵抗諸如時間縮放、隨機剪切、抖動等去同步攻擊。

2)基于同步不變特征的穩健音頻水印

同步不變特征方案以其原理簡單、性能穩定等優點而受到人們普遍重視。該類水印方案的基本思想是將水印信息隱藏在原始載體音頻信號具有同步不變性的量中，而目前所使用的同步不變量主要包括二進小波變換（DYWT,dyadic wavelet transform）、幾何不變矩、直方圖、奇異值、向量范數等[7-9]。在含水印音頻遭受各種攻擊后，同步不變量由于具有同步不變特性不會發生變化，因此隱藏于其中的數字水印信號得以保存。但目前該類水印方案僅僅能夠抵抗輕微的全局音調伸縮和整體時間縮放，尚不能有效抵抗諸如抖動、局部變調、隨機剪切等較復雜的局部去同步攻擊。

3)基于擴頻水印擴頻碼相結合的穩健音頻水印

擴頻數字水印技術往往先利用糾錯編碼技術，對水印信號進行編碼預處理；然后利用正交頻分復用、相移鍵控、移頻鍵控等調制方法，對數字水印信號進行頻譜擴展；最后在原始載體音頻的變換系數中疊加擴頻水印信號[10-11]。擴頻水印擴頻碼相結合算法的優勢在于不需要額外同步信號，且能夠有效抵抗諸如幅度伸縮等輕微全局去同步攻擊。但其仍然存在2個問題，一是由于其缺乏必要的同步保護機制，故普遍難以抵抗局部變調、隨機剪切、抖動等破壞性較強的局部去同步攻擊；二是無法實現數字水印信號的盲檢測，不利于應用。

4)基于同步碼的穩健音頻水印

基于同步碼的音頻水印方案需同時嵌入數字水印信號和同步碼信息。進行水印檢測時，首先檢測到同步碼信息，然后再根據同步碼信息確定出水印信號的嵌入位置。顯然，這類數字音頻水印方法的穩健性和安全性主要依賴于同步碼信息。總體說來，基于同步碼的音頻水印方案具有一定的抵抗諸如整體時間縮放等輕微去同步攻擊能力，但其無法有效抵御諸如局部變調、隨機剪切等局部去同步攻擊，且數字水印容量受到一定限制。此外，同步碼音頻水印算法還會產生2個嚴重問題，一是安全性問題，二是虛警問題。原因是當一個同步標記被用于一系列不同數字音頻作品時，其很容易被敵人發現和去除[12-13]。

5)基于音頻重要特征的穩健音頻水印

基于載體內容局部特征的數字水印方案，其基本思想為，利用相對穩定的載體特征點（也稱顯著點，salient point）來標識水印嵌入位置并確定相對應的特征區域用以嵌入水印信息。在檢測含水印音頻信號時，同樣利用載體特征點進行定位和提取水印信息，從而有效抵御破壞性較強的去同步攻擊。Wang 等[14]結合人類聽覺掩蔽特性，提出了一種基于載體音頻內容的新能量特征點提取方法。該算法具有一定的抵抗噪聲干擾等常規攻擊能力及輕微剪切攻擊能力，但無法有效抵抗時間縮放、音調伸縮、DA/AD 轉換等去同步攻擊能力。Li 等[15]首先提取出原始載體音頻包絡的峰值點，然后以此作為音頻特征點并從原始載體中選取4096個局部音頻片段用于水印信號嵌入，最后利用FFT 在每個局部音頻片段內獨立嵌入數字水印信號。該算法可抵抗輕微的時間縮放、隨機剪切等去同步攻擊，但對高通濾波等常規音頻處理比較敏感，而且無法有效抵御聯合攻擊。Ma 等[16]結合獨立分量分析理論，選取數字音頻能量峰值點作為特征標識并依此確定數字水印嵌入位置，而數字水印信號被嵌入子采樣后的音頻載體內，該算法對噪聲添加、重新采樣等常規音頻處理非常敏感。鮑德旺等[17]首先利用非下采樣小波分解所得的低頻信息重構出新載體數字音頻，然后根據數字音頻的局部能量特征，從新載體中提取出穩定的音頻特征點，并以音頻特征點為標識提取出長度固定的局部音頻段，最后利用量化調制方法將水印信息嵌入局部音頻段內。該算法具有較好的抗噪聲干擾能力，但其抵抗時間縮放、音調伸縮、DA/AD 轉換等攻擊能力較弱。Pun 等[18]提出了一種自同步小波域數字音頻水印方案，該方案利用音頻載體信號的局部方差不變特性來定位水印嵌入位置，具有較好的抵抗常規音頻信號處理及輕微剪切攻擊能力，但對DA/AD 轉換、音調伸縮、時間縮放等比較敏感。Pun 等[19]提出了一種基于穩健不變音頻特征點的檢測方法，利用SWT（stationary wavelet transform）系數的平移不變性、不可感知性和穩健性嵌入水印信息。該算法在空域內提取特征點，與頻域相比抵抗攻擊能力較差，并且該算法是選取特征點周圍的固定長度作為待嵌入水印特征區域，而不是根據特征點周圍的局部特征從而自適應確定待嵌入水印特征區域大小，水印容量與其他算法相比也相對較小。Yuan 等[20]首先在空間域內提取出載體音頻的局部能量峰值點，并將其作為穩定的數字音頻特征點，然后以音頻特征點為標識，確定固定尺寸的局部音頻段，最后對局部音頻段進行小波變換，并利用量化調制技術將水印信息嵌入低頻子帶內，該方法計算簡單、容易實現，但其抵抗噪聲干擾、時間縮放、音調伸縮等攻擊能力均較差。Xiang 等[21]提出了一種基于DCT（discrete cosine transform）域的大容量穩健水印檢測方法，利用DCT 系數的不可感知性和穩健性嵌入正交PN 序列作為水印信息，該算法在提高算法穩健性的同時，保證了較高的水印負載能力。

此外，近年來已有學者將深度學習方法應用到數字水印技術中，對基于深度學習的水印方法進行了深入的研究，以尋求不可感知性及同時抵抗常規信號處理操作和去同步攻擊的穩健性之間的平衡為優化目標，利用粒子群優化等技術設計音頻水印優化過程，自動確定水印算法的最優水印參數和搜索最合適的嵌入位置等，為所設計的水印系統提供了更大的靈活性[22-23]。

綜上所述，窮舉搜索、構造同步不變特征、擴頻水印擴頻碼相結合、同步碼等方案難以有效解決諸如抖動、局部變調、隨機剪切等較復雜的局部去同步攻擊問題，而基于音頻重要特征的數字音頻水印方案為去同步攻擊問題提供了一些可行而有效的解決方向，但現有該類方案普遍存在諸如特征點穩定性差且分布極不均勻、計算量偏大、時間復雜度較高等一系列問題，從而嚴重影響了數字水印的穩健性和不可感知性，大大降低了整個數字音頻水印系統的工作性能。鑒于此，本文提出了一種基于穩健特征點的平穩小波域音頻水印算法。該算法首先利用高斯濾波技術計算出平穩小波域低頻子帶的一階平滑梯度響應，并結合平滑梯度響應分布確定基準閾值，進而提取出分布均勻且性能穩定的音頻特征點；然后以音頻特征點為標識，結合短時能量[24]自適應確定適合于水印嵌入的局部特征音頻段；最后利用擴展抖動調制方法[25]將水印信息嵌入局部特征音頻段中。實驗結果驗證了該算法不僅不可感知性良好，并且對常規音頻信號處理和局部去同步攻擊均具有較好的穩健性。

2 平穩小波變換簡介

與DWT 相比，平穩小波變換（SWT,stationary wavelet transform）[26]具有平移不變性和冗余性等特性，可以對連續小波變換做出更加近似的估計。在音頻信號進行分解時，DWT 采用下采樣抽樣，并采用差值補0的方法對音頻信號進行重構；而SWT在進行音頻信號分解時采用非下采樣抽樣，將信號分解成一系列與原信號長度相同的近似系數和細節系數，同時在每2個濾波器系數之間插入零值以實現濾波器的延拓，從而避免在音頻信號進行重構時產生Gibbs 震蕩現象。

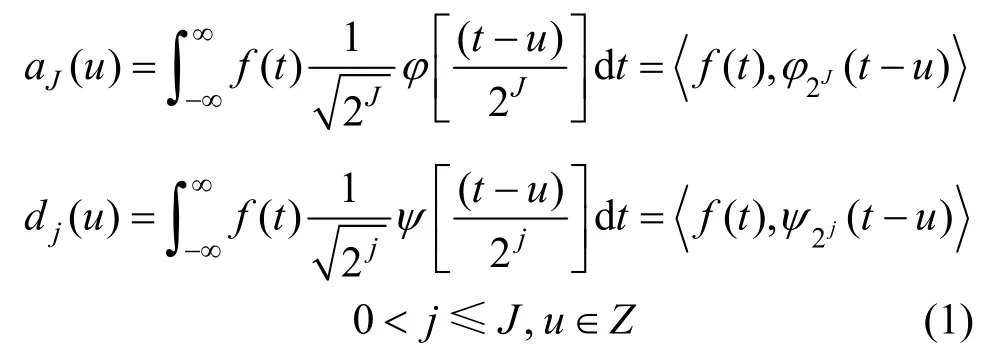
其中，a J(u)為近似系數或低頻系數，d j(u)為細節系數或高頻系數。對于j≥0，則有

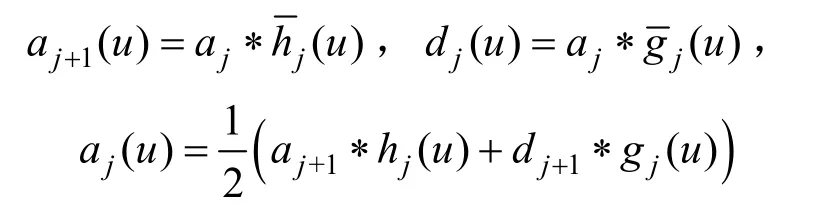
其中，h(n)、g(n)為小波函數ψ(t)對應的共軛鏡像濾波器組，hj(n)為在h(n)相鄰兩項之間插入2j-1個0得到的擴展濾波器。不同于DWT，SWT 并未將每個分級得到的近似系數和細節系數納入到下采樣范圍中，故變換后的近似系數和細節系數能夠保持與原始信號相同的長度。進行SWT 操作可以得到每個分級的低通和高通濾波系數，此操作相當于擴頻操作。隨著分級層數的增加，SWT 系數的分辨率隨之下降，利用濾波器，可以均勻地進行下采樣操作并進一步分級低通系數（二次分級）。SWT的結構如圖1所示。

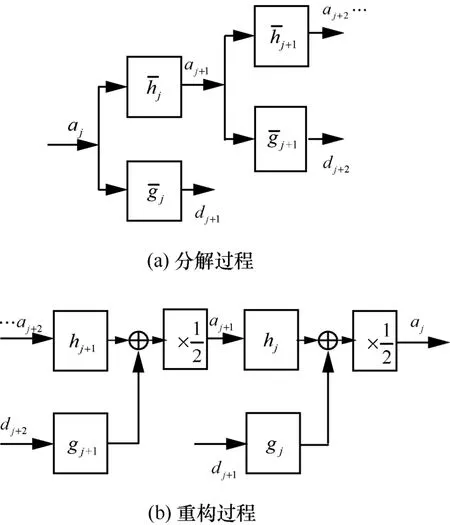
圖1 SWT 的結構

為證明SWT 的有效性，圖2給出了數字音頻的3級SWT 分解/重構示意。其中，圖2(a)為原始音頻，圖2(b)為3級小波分解的低頻子帶，圖2(c)～圖2(e)分別為3級小波分解的尺度3、尺度2和尺度1高頻子帶，圖2(f)為小波重構音頻，圖2(g)為小波重構音頻與原始音頻的差值。

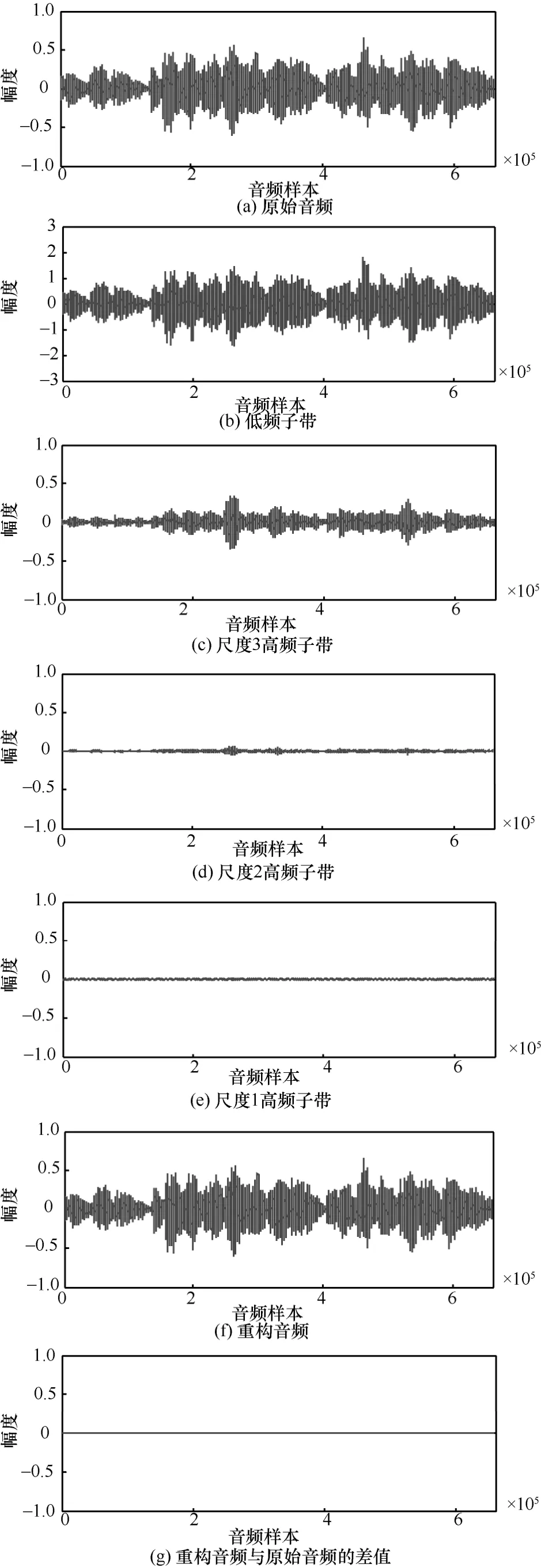
圖2 數字音頻的3級非下采樣小波分解/重構示意

觀察圖2可以看出，數字音頻經過3級SWT 分解后再重構，重構波形與原始音頻波形基本保持一致。

3 基于平滑梯度的音頻特征點提取

特征點提取是基于載體內容局部特征的數字音頻水印方案的關鍵環節之一。目前，可應用于數字音頻水印領域的音頻特征點檢測算子包括樣本峰值法、包絡峰值法[14-22]。然而，以上音頻特征點檢測算子均直接采用音頻樣本值刻畫局部數字音頻性質，其不可避免存在2個方面的問題：一方面，特征點檢測算子對音程跳躍幅度較大的“高”音調區很敏感，會在“高”音調區域檢測出很多“噪聲”特征點；另一方面，特征點過于集中在高頻泛音充分的“尖”音色區。也就是說，利用現有檢測算子所提取出的音頻特征點，普遍存在穩定性差且分布極不均勻的問題，嚴重影響數字音頻水印對DA/AD 轉換、隨機剪切、抖動等攻擊的抵抗能力。盡管Dessein 等[27]結合最大似然參數估計理論，提出了一種基于廣義似然比極值的數字音頻特征點檢測算法，但由于其所采納的樣本指數分布假設并不適合大多數實際音頻，故該算法的音頻特征點檢測性能較低。此外，該特征點檢測算法的時間復雜度較高，不利于實際應用。

本文將利用描述能力強且性能穩定的平滑梯度刻畫局部數字音頻性質，進而提出一種基于平滑梯度的平穩小波域音頻特征點提取方法，可以很好地滿足音頻水印的要求。

假設A={a(x),1≤x≤L}表示原始數字音頻信號，其中L為音頻的樣本數，a(x)∈{0,1,2,…,(2p-1)}表示每個樣本的幅值，p表示每個樣本的量化位數，則基于平滑梯度的音頻特征點提取方法如下。

步驟1SW 變換。對原始載體音頻A進行3級SWT 分解，以得到一個低頻子帶F和若干個高頻子帶。本文選取抗噪能力較強的低頻子帶提取音頻特征點。

步驟2音頻梯度計算。利用式(2)，計算出低頻子帶F(x)={f1,f2,…,fx,…,fL}的一階梯度其中，音頻梯度值

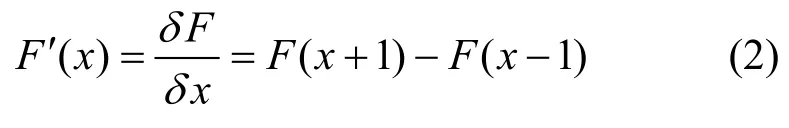
步驟3平滑處理。利用式(3)，對一階音頻梯度進行高斯濾波處理，以得到性能穩定的一階平滑梯度

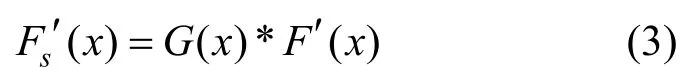
步驟4響應計算。利用一階平滑梯度幅值，計算出原始音頻樣本a(x)的響應值R(x)，并以此刻畫局部數字音頻性質。音頻樣本a(x)的局部響應值R(x)為

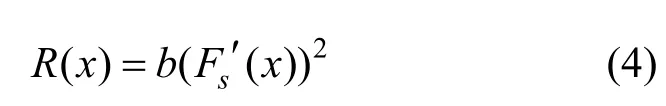
這里，b為任意常量，實驗中b=0.5。

步驟5特征點提取。對音頻樣本響應值R(x)={r1,r2,…,rx,…,rL}進行降序排列得到PR={Pr_L,Pr_L-1,···,Pr_1}，濾掉位于首尾兩端的音頻樣本，確保有足夠的空間可以嵌入完整水印信息，即不滿足

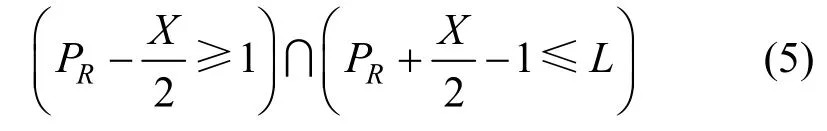
其中，X代表相鄰特征點之間的基本間距，本實驗中，X=1.5×104。

以最高響應值Pr-x為基準設置閾值，濾掉與其相鄰過近的特征點，從而確保提取出的特征點分布均勻，即不滿足

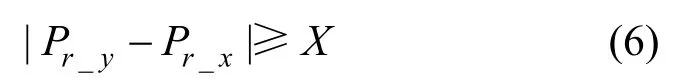
其中，Pr_y∈{Pr_x-1,Pr_x-2,···,Pr_1}，選取前Y個點Pr∈{P1,P2,···,PY}作為本方法的音頻特征點即同步標記，本實驗中，Y=13。

圖3給出了本文特征點提取方法抵抗常規信號處理和去同步攻擊的部分實驗結果。其中，“○”表示正確提取，“●”表示錯誤提取（本實驗中，特征點位置偏移5個樣本以上即視為錯誤點）。

4 數字水印嵌入與檢測算法

4.1 數字水印的嵌入

本文采用冗余嵌入策略，提出了一種基于穩健特征點的平穩小波域數字音頻水印算法，水印嵌入的關鍵步驟可描述如下。

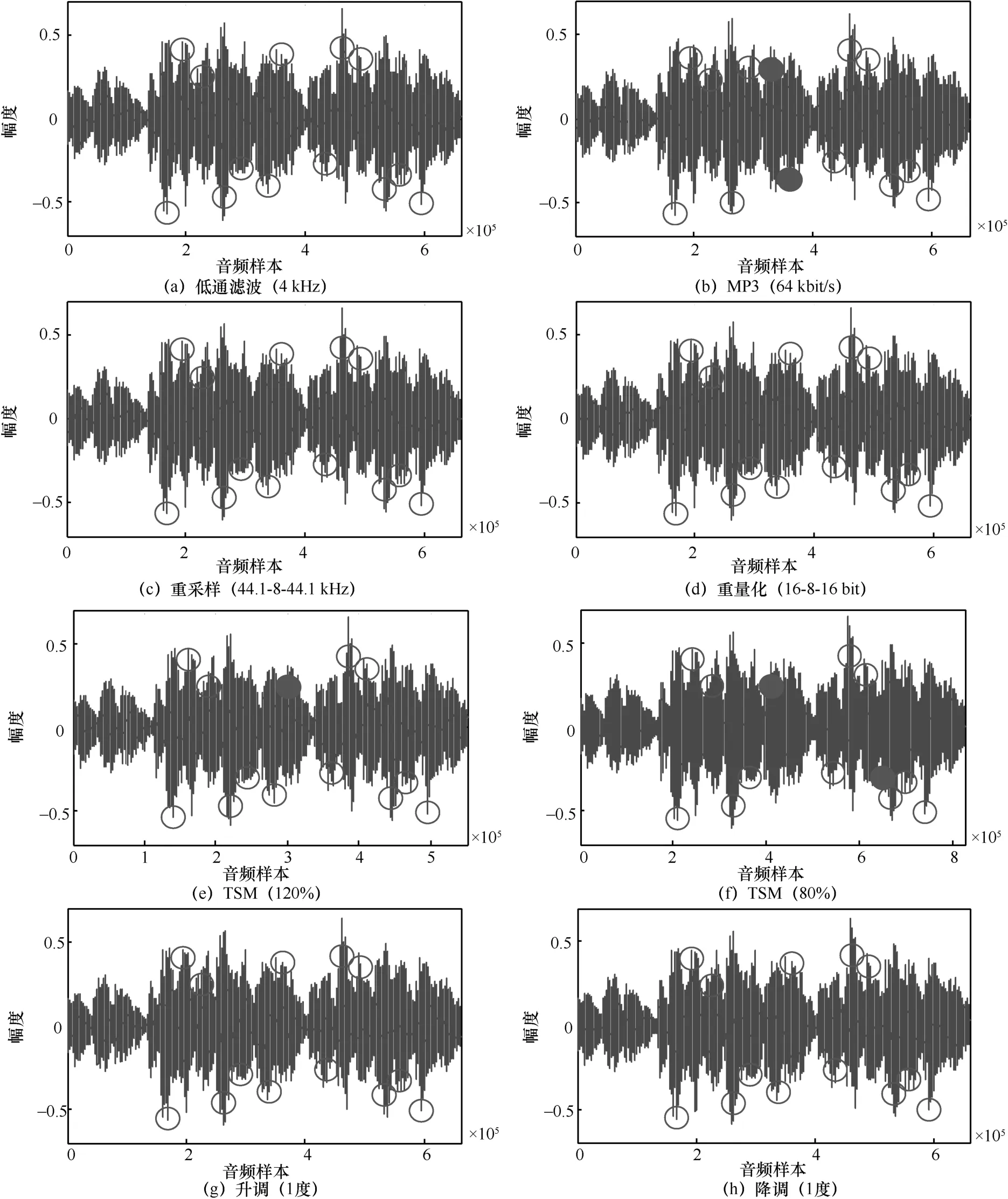
圖3 各種攻擊下的音頻特征點提取

步驟1數字水印產生。由密鑰K產生一個偽隨機序列C={c(i),i=1,···,s}作為數字水印信息，其中，s為水印大小，c(i)∈{0,1}。

步驟2音頻特征點提取。利用基于平滑梯度的平穩小波域音頻特征點檢測算子，從原始音頻載體A中提取音頻特征點，以得到音頻特征點集Pr∈{P1,P2,···,PY}。

步驟3局部特征音頻段構造。所謂局部特征音頻段，是指以數字音頻特征點為標識，從原始載體音頻中分割出的一部分子音頻，以其作為水印信號的嵌入和檢測區域。本文局部特征音頻段的具體構造過程如下。

1)將載體音頻信號A進行降序排列，得到載體音頻數據最大值Amax與最小值Amin，并歸一化到[-1,1]的范圍，具體計算式為

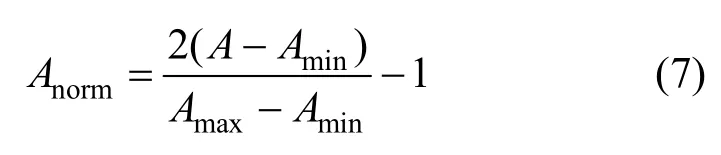
其中，Anorm是歸一化后的音頻信號。

2)對Anorm進行3級SWT 分解，以得到一個低頻子帶F1和若干個高頻子帶。

3)在低頻子帶F1下，以特征點Pr為標識，循環統計每個特征點Pr左右窗口長度為M范圍內的能量和，用以代表特征點周圍音頻短時能量。于是，短時能量可表示為[24]

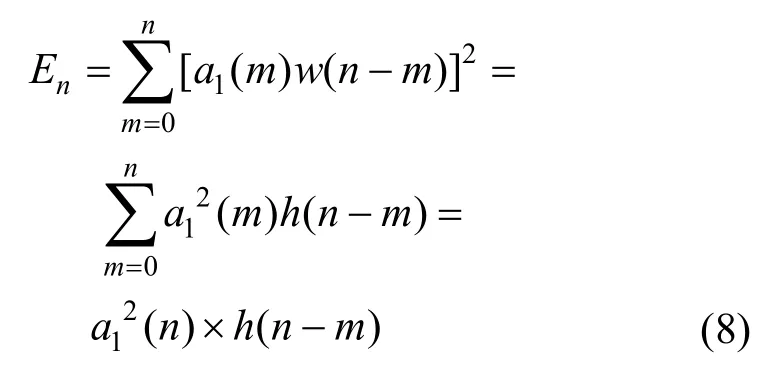
其中，En表示n時刻音頻信號a1(n)的短時能量，w(n-m)表示窗函數，h(n)=w2(n)，n=1+2M。本文選取的窗函數為漢寧窗w(n)，即

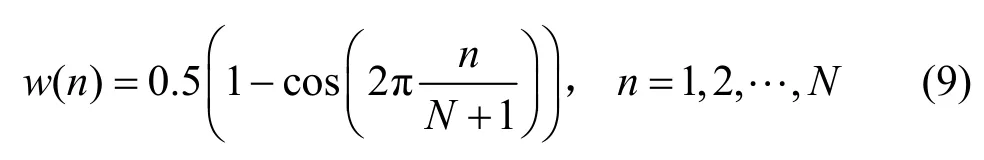
其中，N表示窗長，特征點Pr周圍的音頻信號集可表示為

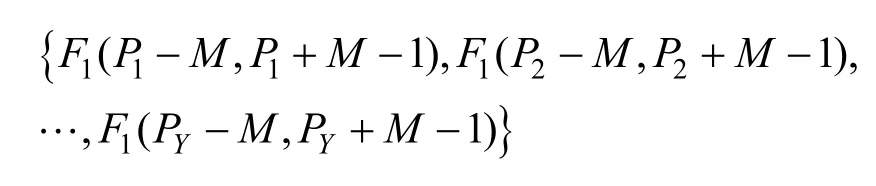
4)利用特征點短時能量集E∈{E1,E2,…,EY}再次計算

5）計算自適應局部特征音頻段，其中，待嵌入水印音頻段長度Dr=E1sK,s為水印大小，K為常數，Dr∈{D1,D2,···,DY}。于是，得到用于水印嵌入的局部特征音頻段集為

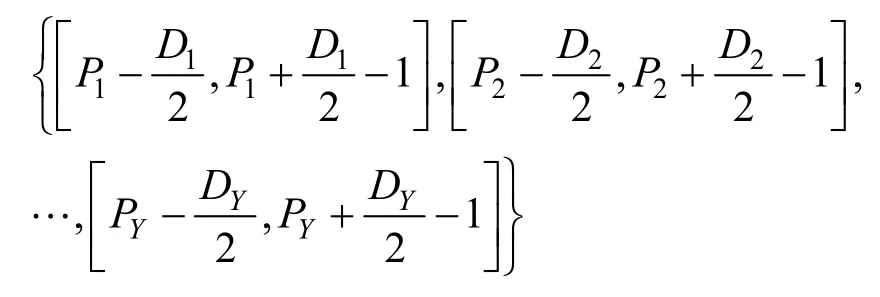
步驟4數字水印嵌入。本文采用量化調制方法，數字水印的具體嵌入過程如下。

1)對載體音頻信號A進行3級SWT 分解，以得到一個低頻子帶F和若干個高頻子帶。本文選取性能穩定的SWT 域低頻子帶嵌入水印信息。

2)在低頻子帶F內，依據特征點Pr和待嵌入水印音頻段長度Dr找到對應的特征區域，并根據水印位的長度s對待嵌入水印的局部特征音頻段進行分段，每段長度為可得到音頻子段

3)量化調制音頻子段a2內的t1個低頻系數，每個音頻子段嵌入一個水印位。首先根據水印信息的值，使用2種不同的抖動量化[25]，自適應確定水印嵌入強度。

①當C=0時，抖動量化Q0為

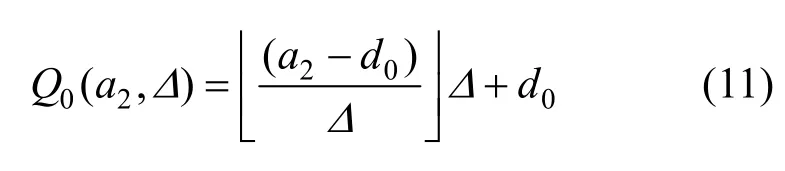
②當C=1時，抖動量化Q1為

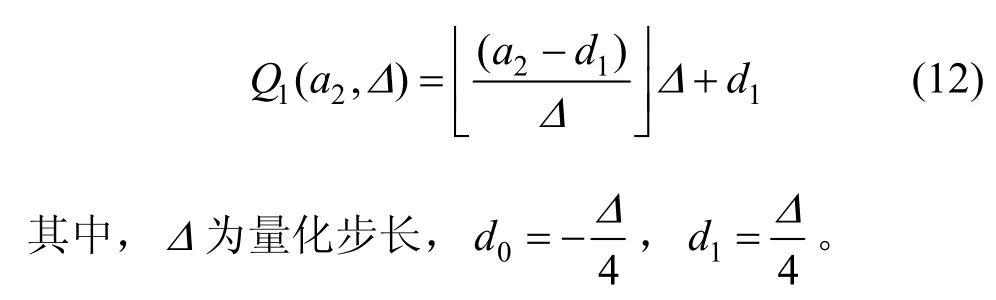
然后將水印信息利用STDM（spread transform dither modulation）量化方法嵌入音頻子段，量化調制方法為[25]

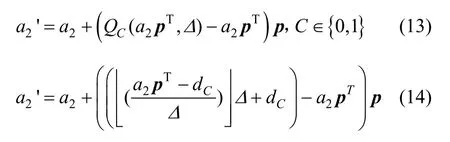
其中，p為投影向量，為嵌入水印后的音頻段。

4)用含水印音頻子段內的低頻系數代替原低頻系數，并進行逆SWT，即可得到含水印局部特征音頻段。

步驟5含水印音頻獲得。重復步驟1～步驟4，直到所有局部特征音頻段都按照上述步驟處理完畢。最后，用含水印局部特征音頻段替換原始的局部特征音頻段，得到含水印數字音頻Aw信號。

4.2 數字水印的檢測

步驟1使用與嵌入過程相同的密鑰K產生原始數字水印序列C={c(i),i=1,···,s}。

步驟2利用基于平滑梯度的平穩小波域音頻特征點檢測算子，從含水印數字音頻Aw中提取音頻特征點，以得到音頻特征點集Prw∈{P1,P2,···,PYw}。

步驟3以所提取的音頻特征點為標識，利用本文局部特征音頻段構造方法，計算出短時能量E2，并根據E2計算出含水印特征音頻段長度Drw=E2sK，s為水印大小，K為常數，Drw∈{D1,D2,···,DYw}，從而得到用于水印提取的局部特征音頻段集為

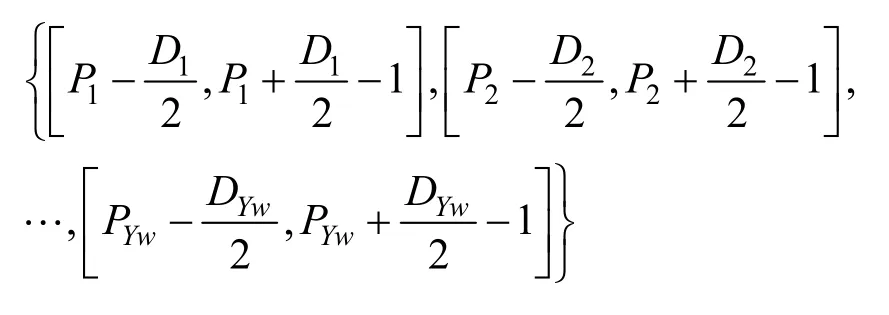
步驟4對含水印數字音頻Aw進行3級SWT分解，并按照如下過程提取水印信息。

1)在低頻子帶Fw內，依據特征點Prw和含水印特征音頻段長度Drw找到對應的特征區域，并根據水印位的長度s對待提取水印的局部特征音頻段進行分段，每段長度為，得到音頻子段∈（每個音頻子段提取一個水印位）。

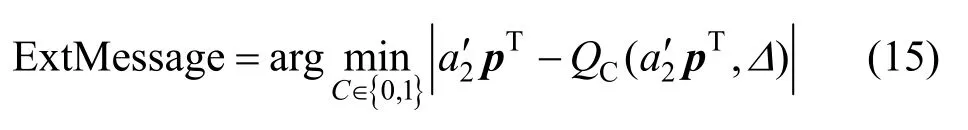
3)重復上述步驟，即可檢測出局部特征音頻段內所隱藏的數字水印序列為

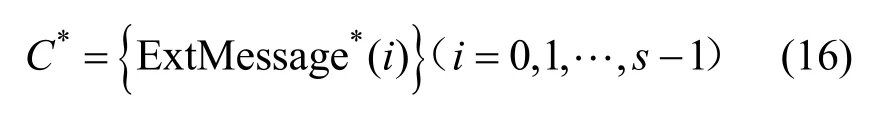
重復步驟4，直到檢測完所有局部特征音頻段。只要有2個以上的局部特征音頻段能夠成功檢測到水印信號，即可認為數字水印檢測成功；否則，水印檢測失敗。

5 仿真實驗與結論

本節分別給出了檢測性能測試以及抗攻擊能力測試的仿真實驗結果。實驗中，選用采樣頻率為44.1 kHz、量化精度為16 bit、長度為15 s 的單聲道數字音頻信號作為原始載體，數字水印采用了128位的偽隨機序列。另外，量化步長Δ=73，檢測閾值Ts=24（即虛警率PF-A ≈5×10-4）。

5.1 不可感知性測試

圖4給出了本文算法的不可感知性能測試結果，包括原始音頻、含水印音頻、差值音頻。從圖4(a)與圖4(b)中可以明顯看出，原始音頻與含水印音頻的波形區別很小，而差值圖4(c)也充分證明了這一觀點。另外，本文算法的PSNR 值為39.8312 dB，客觀結果充分證明了本文算法的不可感知性良好。

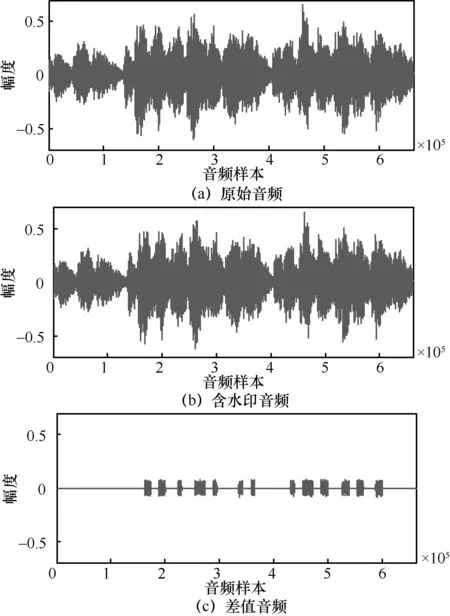
圖4 數字音頻水印的不可感知性能測試結果

5.2 穩健性測試

為了驗證本文數字音頻水印算法的穩健性能，仿真實驗分別對本文算法和文獻[19-21]算法的含水印音頻進行了一系列攻擊。其中，文獻[19-20]算法均是利用了平滑梯度刻畫了局部數字音頻性質，針對如何有效解決數字音頻水印算法的局部去同步攻擊問題展開研究，因此本文首先與文獻[19-20]算法進行了性能比較。文獻[21]算法為較新的具有代表性的基于擴頻水印擴頻碼相結合的數字音頻水印方法。圖5和圖6分別給出了本文算法抵抗常規信號處理和去同步攻擊的實驗結果。其中，分子表示從攻擊后含水印數字音頻中成功檢測到水印信號的局部特征音頻段數目，分母表示原始載體音頻中嵌有水印信號的局部特征音頻段數目。這里，定義每個完整水印信息正確提取位數多于，即視為該自適應特征音頻段的水印被正確提取。本實驗中，利用RCES（the ratio of correctly extracted segment）表示自適應特征音頻段水印的正確提取率，正確提取的含水印局部特征音頻段選用淺色填充“”，錯誤提取的含水印局部特征音頻段選用深色填充“”。表1和表2、圖7和圖8給出了本文算法和文獻[19-21]算法的穩健性能對比。

表1和表2給出了各種攻擊下本文算法與文獻[19-20]的對比結果，圖7和圖8顯示了本文算法與文獻[21]算法在相同原始音頻載體條件下，抵抗常規攻擊和去同步攻擊的對比結果。從對比結果可以看出，本文算法實驗結果整體好于文獻[19-21]，進一步證明了本文算法具有良好的穩健性。

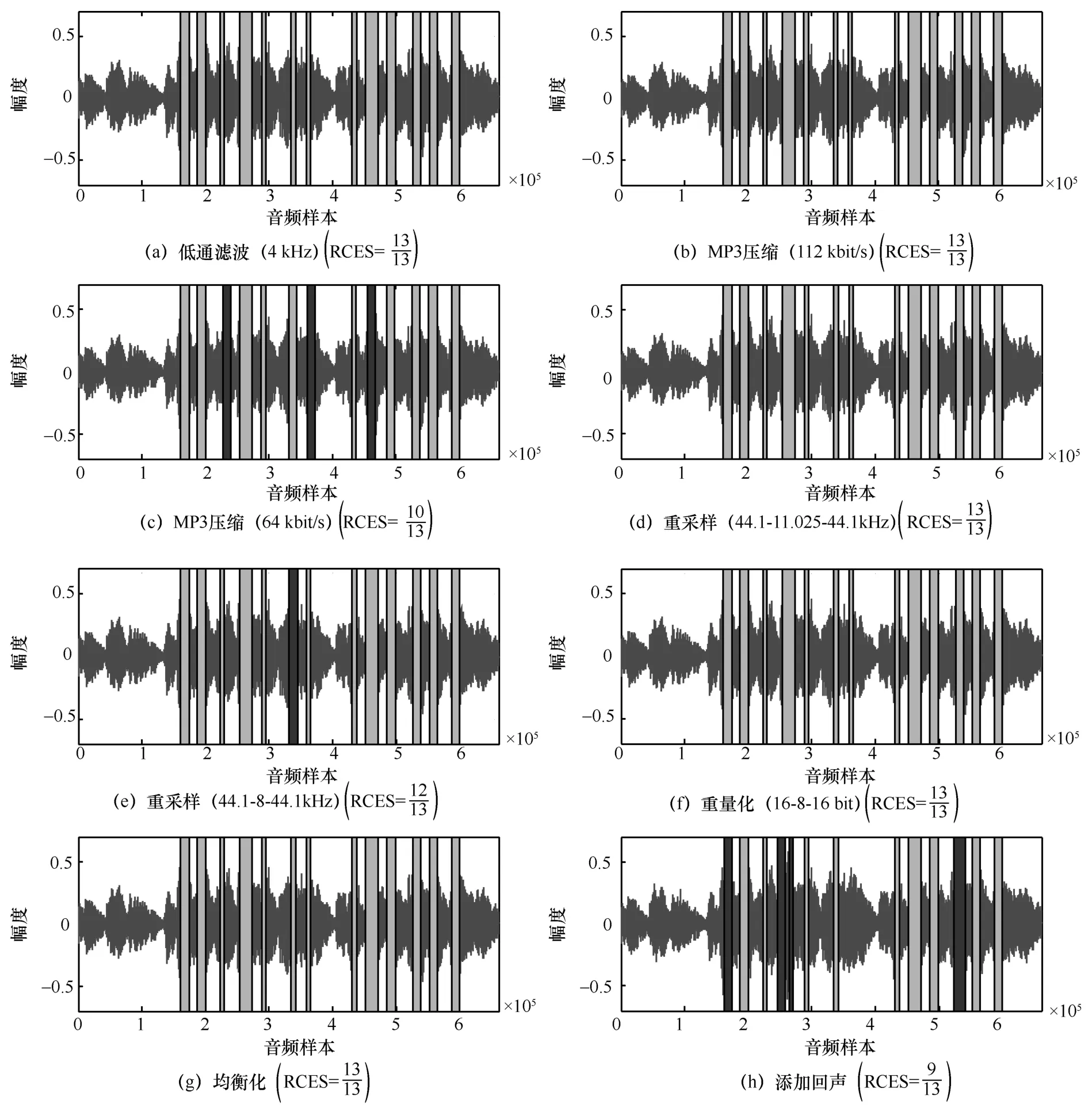
圖5 本文算法抵抗常規音頻信號處理的實驗結果

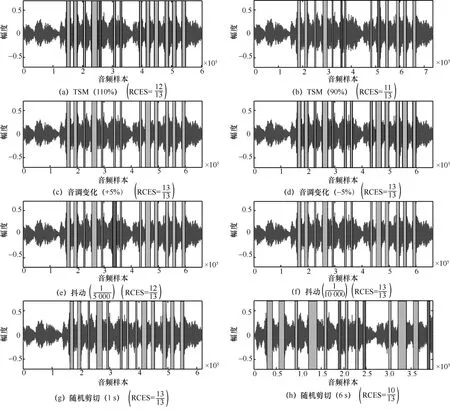
圖6 本文算法抵抗去同步攻擊的實驗結果

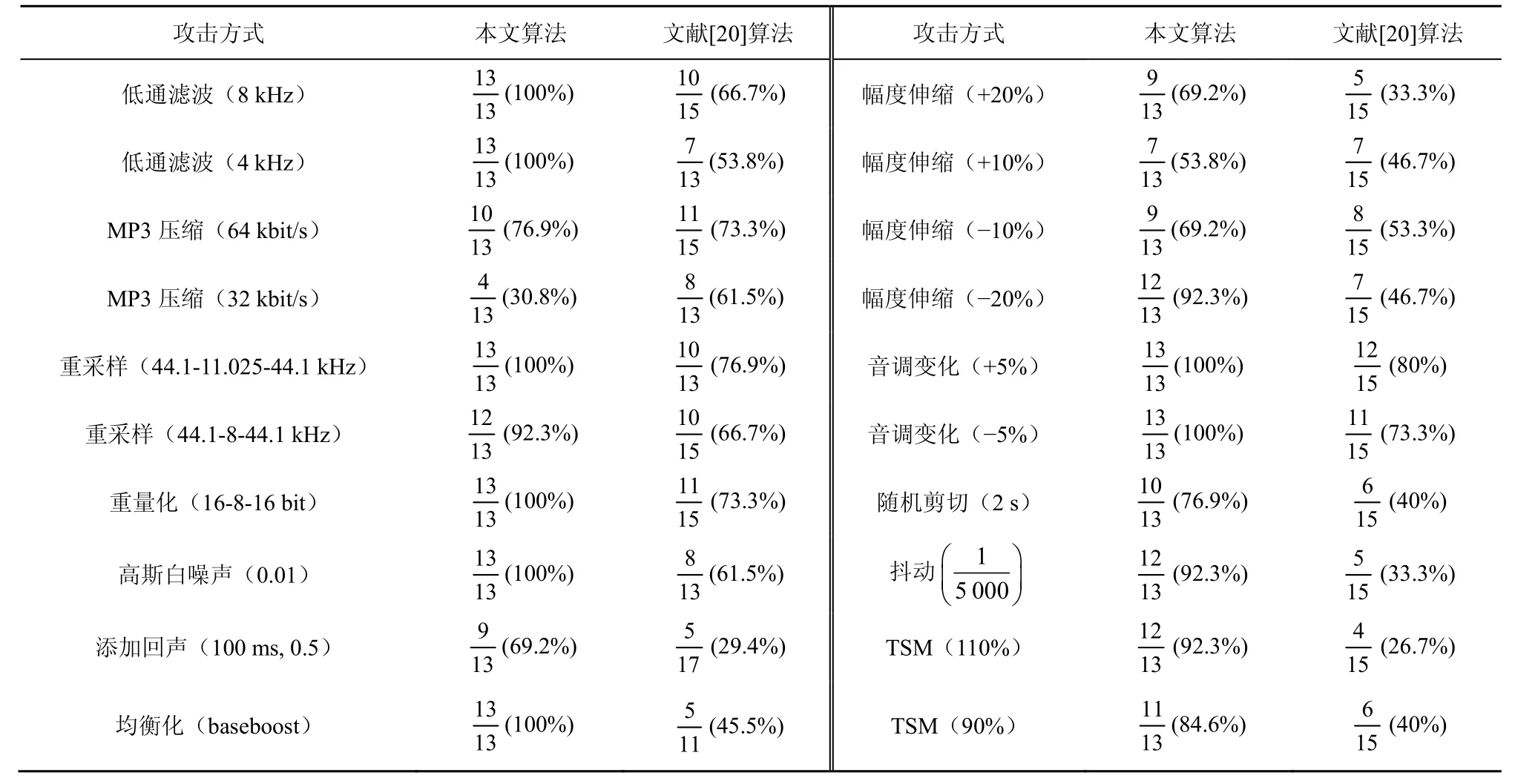
表1 本文算法和文獻[20]算法的穩健性能對比結果

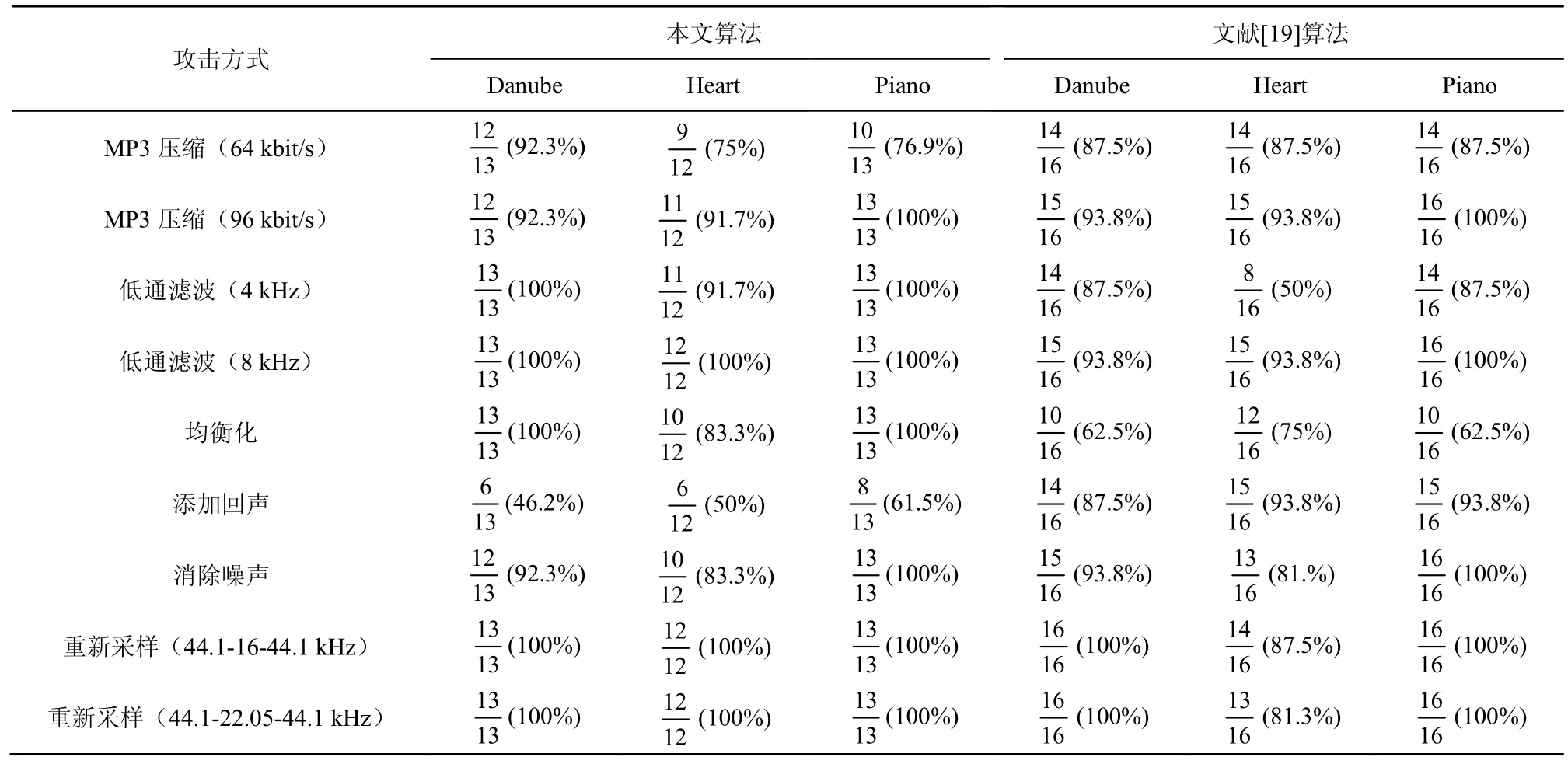
表2 本文算法和文獻[19]算法的穩健性能對比結果

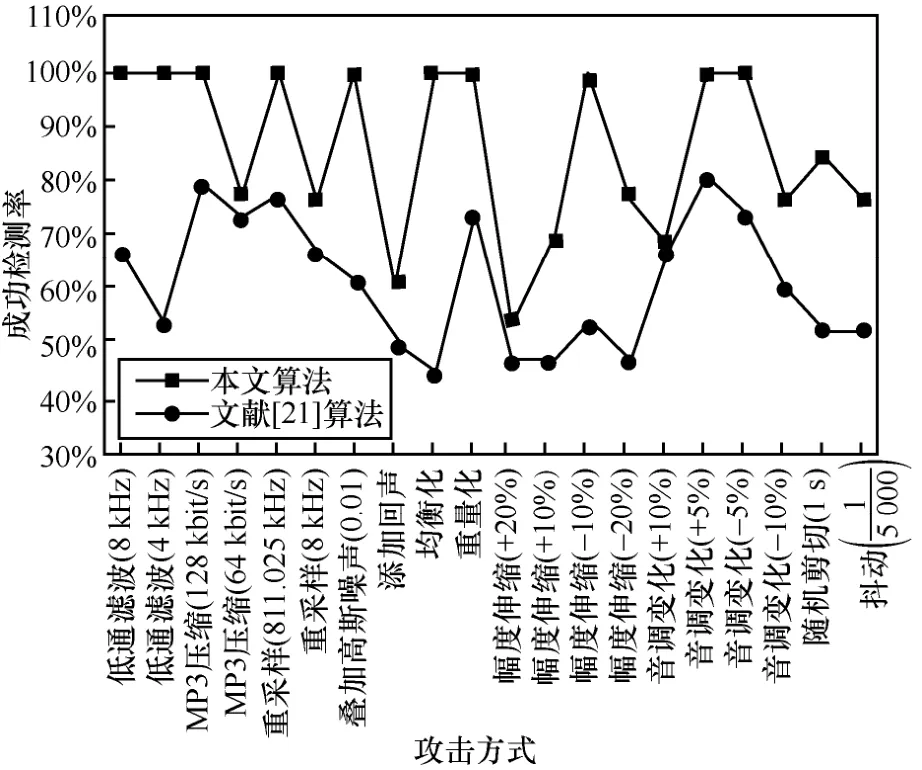
圖7 本文算法和文獻[21]算法的穩健性能對比結果（’Piano.wav’）

6 結束語

數字水印是解決數字作品版權保護與內容認證的有效辦法之一，穩健性是數字水印算法的重要性能指標之一。但現有絕大多數音頻水印在經受去同步攻擊后難以生存。因此，研究可有效抵抗去同步攻擊的強穩健數字音頻水印理論與方法仍是一項富有挑戰性的工作。本文提出了一種基于穩健特征點的平穩小波域音頻水印算法，實驗結果表明，本文數字音頻水印算法不僅具有較好的不可感知性，而且對常規音頻信號處理（包括重采樣、重量化、MP3壓縮、均衡化等）和去同步攻擊（包括隨機剪切、幅度伸縮、局部變調、抖動等）均具有較好的穩健性。

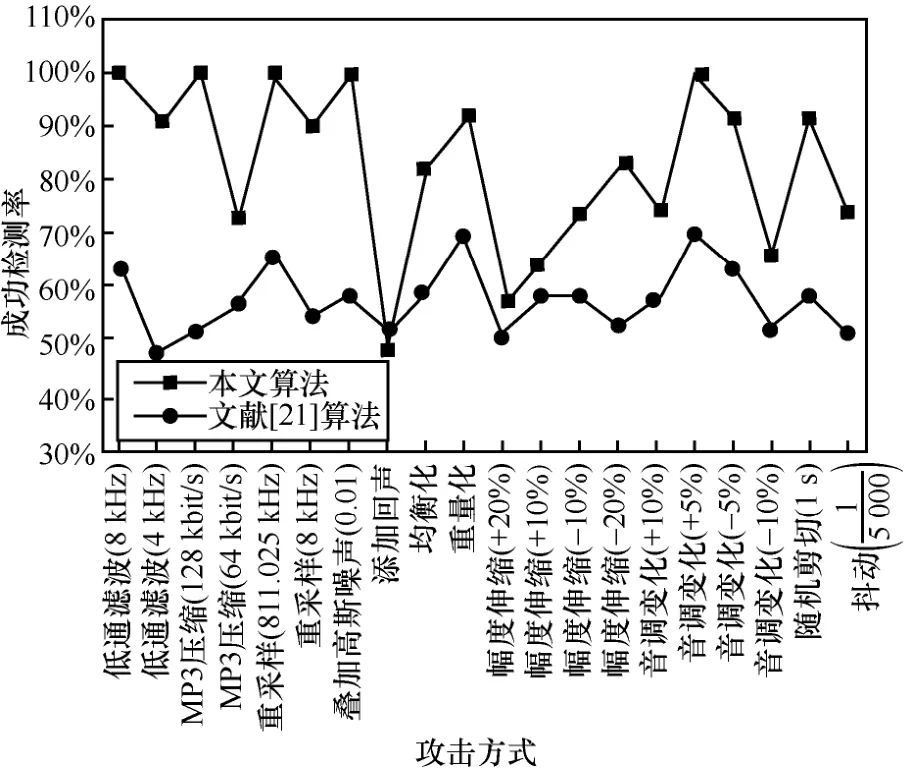
圖8 本文算法和文獻[21]算法的穩健性能對比結果（’Heart.wav’）