高考全國卷立體幾何命題動向分析

■廣東省汕頭市澄海華僑中學 潘敬貞

一、近三年試題特點分析

題型上,近三年高考全國卷對立體幾何的考查題型有選擇題、填空題及解答題。題量上,多數以 “兩小一大”為主,偶有 “一小一大”,如2018年全國Ⅰ卷有 “三小一大”共27分,而2019 年全國Ⅰ卷才“一大一小”共17分,所以說題量并不是固定的,有時有微調。

知識點分布上,小題主要考查點線面的位置關系與數量關系,求體積、面積等知識,部分試題滲透數學文化、實際背景及知識交匯處命題,突出試題的思想性和知識點的實際應用價值,主要考查同學們的直觀想象、邏輯推理、數學運算、數學抽象等核心素養。另外2019年全國9套試卷均未考查三視圖,這與新課改中要求刪除三視圖有一定關系,但2020 年高考的命題仍按老課標與老教材進行命題,沒有任何信息表明2020年高考不考三視圖,因此在備考時一定要注意。立體幾何解答題一般位于17～20題的位置,題型比較常規,第一小題重點考查線線、線面、面面的位置關系的證明,第二小題理科主要考查空間角,文科主要考查求錐體的體積、表面積等問題,要求同學們對基本概念的掌握要清晰,并且具備一定的運算能力。

難度上,小題以容易題和中檔題為主,也有壓軸小題,比如2018年全國Ⅰ卷理科第12題,2019年全國Ⅰ卷理科第12題,2017年全國Ⅰ卷理科第16題。解答題基本上是以中檔題為主。

二、考查問題分析

高考全國卷立體幾何的小題主要考查以下幾個方面的問題:(1)幾何體中的線面位置關系、數量關系,主要情形有:①已知一個球及其內接或外切的幾何圖形求其中的數量關系;②已知一個多面體中的位置或數量關系求其他的數量關系。(2)根據某幾何體的三視圖猜想其幾何特征并求該幾何體的某個數量關系,主要情形有:①給出幾何體的三視圖,通過看圖、想圖和畫圖得到其直觀圖,以此確定其幾何特征并求其有關數量;②根據三視圖的條件確定直觀圖所表示的幾何體的幾何特征,計算難度很低,一般是求能反映幾何體本身特征的量,并且只要求代公式直接求值。

解答題常考查證明和求解其他線面位置關系和數量關系,主要情形有:①根據幾何體的部分線面位置關系及數量關系,通過轉化、推理、計算,從而證明和求解其他線面位置關系和數量關系,具體呈現為:證明異面直線垂直、線面垂直、面面垂直、線面平行、面面平行,求幾何體的體積、表面積,點到面的距離等;②通過建立空間坐標系,利用向量運算求幾何體中的空間數量關系。

三、高考動向透視

隨著新課標的頒布,高考命題也發生了微妙的變化,試題凸顯以基本知識為載體,考查同學們的核心素養。主要是以立體幾何的基本概念、基本知識、基本幾何體為載體,通過想圖、畫圖、用圖的過程考查同學們的直觀想象與數學抽象;通過判斷或證明點、線、面的位置關系考查同學們的邏輯推理;通過求線面的數量關系考查同學們的數學運算等核心素養。選擇題與填空題由于不給幾何圖形,同學們必須通過想圖、畫圖、用圖等一系列過程方可順利解決有關問題,這樣更好地考查同學們的直觀想象與數學抽象等核心素養。由于受到已知圖形的限制,因此解答題更側重于考查同學們的邏輯推理、數學運算與數學建模等核心素養。當然,有些試題具有較強的綜合性,同一道試題既考查數學抽象又考查邏輯推理,還考查數學運算。

1.分析幾何體中的位置關系

例1(2019年全國Ⅱ卷文理7)設α,β為兩個平面,則α∥β的充要條件是( )。

A.α內有無數條直線與β平行

B.α內有兩條相交直線與β平行

C.α,β平行于同一條直線

D.α,β垂直于同一平面

答案:B。

評注:本題結合充要條件考查線面位置關系,由于沒有已知圖形,也不需要運算,考生全憑自己掌握的立體幾何基本知識通過想象解決問題,主要檢測考生運用直觀感知、操作確認、推理論證解決立體幾何問題的關鍵能力,這類題有一定的難度,要注意掌握好基礎知識,提升自己解決問題的能力。

2.分析幾何體中的幾何關系并求其中的數量關系

(1)已知一個球及其內接或外切的幾何圖形求其中的數量關系。

例2(2018年新課標Ⅲ卷文12理10)設A,B,C,D是同一個半徑為4的球的球面上四點,△ABC為等邊三角形且其面積為9則三棱錐體積的最大值為( )。

答案:B。

評注:解答本題,首先是想圖和畫圖,再分析體積表達式中不變的量是三棱錐底面的面積,變量只有三棱錐的高,即三棱錐高的最大值是球心到底面的距離加上球的半徑,進而將問題轉化為求球心到截面的距離,構造直角三角形易得其解。主要考查直觀想象、數學抽象、數學建模、數學運算等核心素養。

(2)已知一個多面體中的位置或數量關系求其他的數量關系。

例3(2018年全國Ⅰ卷文10)在長方體ABCD-A1B1C1D1中,AB=BC=2,AC1與平面BB1C1C所成的角為30°,則該長方體的體積為( )。

答案:C。

評注:本題以長方體為載體,考查線面夾角的概念,建立關于線面夾角的數學模型,求出長方體的棱長,從而求出長方體的體積。主要考查直觀想象、數學建模、數學運算等核心素養。

例4(2017年新課標Ⅰ卷理16)如圖1,圓形紙片的圓心為O,半徑為5 cm,該紙片上的等邊△ABC的中心為O。D,E,F為 圓O上 的 點,△DBC,△ECA,△FAB分別是以BC,CA,AB為底邊的等腰三角形。沿虛線剪開后,分別以BC,CA,AB為折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱錐。當△ABC的邊長變化時,則所得三棱錐體積(單位:cm3)的最大值為____。

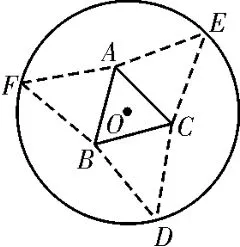
圖1

評注:本題主要結合導數工具求三棱錐體積的最大值,首先要分析數量關系,建立關于體積的數學模型,再利用導數工具進行解決。本題具有一定的綜合性、靈活性、創新性,主要考查直觀想象、數學抽象、數學建模、數學運算等核心素養。

3.根據某幾何體的三視圖猜想其幾何特征并求該幾何體的某個數量關系

例5(2017 年新課標Ⅱ卷文6 理4)如圖2,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分后所得,則該幾何體的體積為( )。

圖2

A.90π B.63π C.42π D.36π

答案:B。

評注:給出幾何體的三視圖,通過看圖、想圖、畫圖得到其直觀圖,以此確定其幾何特征并求其有關數量。 這類問題主要考查由三視圖得到直觀圖的空間想象能力;其次是根據三視圖的條件確定直觀圖所表示的幾何體的幾何特征;計算難度比較低,一般是求能反映幾何體本身特征的量,并且只要求代公式直接求值。 主要以考查簡單組合體與殘缺體為主。

4.證明和求解其他線面位置關系和數量關系

(1)根據幾何體的部分線面位置關系及數量關系,通過轉化、推理、計算,從而證明和求解其他線面位置關系和數量關系。

例6(2017 年新課標Ⅰ卷文18)如圖3,在四棱 錐P-ABCD中,AB∥CD,且 ∠BAP= ∠CDP=90°。

圖3

(1)證明:平面PAB⊥平面PAD;

(2)若PA=PD=AB=DC,∠APD=90°,且四棱錐P-ABCD的體積為,求該四棱錐的側面積。

評注:本題主要考查空間幾何體的面面垂直的證明、求四棱錐的側面積等知識,意在考查考生的空間想象能力、化歸轉化能力、運算求解能力。第一問欲證平面PAB⊥平面PAD,只需要證明AB⊥平面PAD,即在平面PAD內尋找兩條相交直線與AB垂直,利用已知條件,即可得證。第二問,利用第一問的結論,可快速求出四棱錐的高,再利用四棱錐P-ABCD的體積為,即 可 求 出AB的長,從而可以求出該四棱錐的側面積。

(2)通過建立空間坐標系,利用向量運算求幾何體中的空間數量關系。

例7(2019年全國Ⅱ卷理17)如圖4,長方體ABCD-A1B1C1D1的底面ABCD是正方形,點E在棱AA1上,BE⊥EC1。

圖4

(1)證 明:BE⊥ 平 面EB1C1;

(2)若AE=A1E,求二面角B-EC-C1的正弦值。

評注:第一問證明線面垂直,主要考查同學們對點線面位置關系的理解、應用及語言表達,屬于同學們較為熟悉的問題。第二問求解二面角的正弦值,屬于常規問題,題目入口寬有利于同學們的解答,注重考查四基與四能,若能用好空間直角坐標系,還可以給試題的解答賦予更優化的方法,關鍵看同學們如何選擇使用。建立空間直角坐標系常用的三條途徑:①利用圖形中現成的垂直關系建立坐標系,當圖形中有兩兩垂直且交于一點的三條直線時,可以利用這三條直線直接建系;②利用圖形中的對稱關系建系,圖形中雖沒有兩兩垂直且交于一點的三條直線,但有一定的對稱關系,利用圖形中的對稱關系可建立空間直角坐標系,這是建立空間直角坐標系解決立體幾何有關問題的關鍵;③利用面面垂直的性質建立坐標系,圖形中有兩個互相垂直的平面,可以利用面面垂直的性質定理作出兩兩垂直且交于一點的三條直線,從而建立坐標系。

四、復習建議

在復習過程中,一要重視基本概念本質的理解,了解概念、公式的來龍去脈。二要正確理解數學符號并規范使用數學符號,包括文字語言、符號語言、圖形語言,要做到三種語言的熟練轉化。對課本上的定理、公理能夠用三種語言表示,對平行、垂直判定方法進行梳理總結,形成系統,用三種語言表示。多多練習命題真假判斷問題,一方面,加深對定理的理解;另一方面,通過畫圖、想圖,培養將文字語言、符號語言轉化為圖形語言的能力。三要有意識地提升畫圖能力,高考中立體幾何小題一般都不給圖,而大題中所給的圖又往往需要添加輔助元素,所以從某種意義上說,作出一個好圖等于題目解決了一半,因此,在復習中注重畫圖能力的提升,訓練中要做到:(1)會畫——根據題設條件畫出適合題意的圖形或畫出自己想作的輔助線(面),作出的圖形要直觀,虛實要分明。(2)會看——根據題目給出的圖形,想象出幾何體的形狀和有關線面的位置關系。(3)會用——對圖形進行必要的分解、組合,或對其某部分進行平移、翻折、旋轉、展開或割補等。四要規范表述,基礎知識、基本技能、基本方法、基礎練習要到位,解題步驟要規范,注重通性通法,體現 “大眾化”。從歷年備考立體幾何解答題的情況來看,很多考生出現“會而不對,對而不全”的問題比較嚴重,很值得引起我們的重視。因此,在平時的訓練中,要養成規范答題的良好習慣,把典型問題的解法總結成程序化的步驟。比如用空間向量解決立體幾何問題的步驟為:合理建系——正確寫出坐標——寫出相關向量——經過向量運算——向量結論——幾何結論。