空間幾何知識結構與拓展

■安徽省利辛高級中學 胡 彬

一、知識結構框架

二、結構分析

立體幾何研究現實世界中物體的形狀、大小與位置關系。通過對立體幾何初步的學習,可以幫助同學們以長方體為載體,認識和理解空間點、直線、平面的位置關系;用數學語言表述有關平行、垂直的性質與判定,并對某些結論進行論證;了解一些簡單幾何體的表面積與體積的計算方法;運用直觀感知、操作確認、推理論證、度量計算等認識和探索空間圖形的性質,建立空間觀念。通過對空間向量與立體幾何的學習,可以幫助同學們在平面幾何的基礎上,運用向量的方法研究基本圖形的位置關系和度量關系,體會向量方法和綜合幾何方法的共性和差異;運用向量方法解決簡單的數學問題和實際問題,感悟向量是研究幾何問題的有效工具。

本部分一直是高考的重點、難點與熱點。一般以基本圖形為載體,利用其定義、性質進行判定、計算,或利用空間向量有效研究立體幾何相關問題。本部分涉及的數學思想主要為函數與方程思想、轉化與化歸思想、分類討論思想。較好地培養了同學們的空間想象能力、推理能力和運算求解能力。考查的核心素養是直觀想象、邏輯推理和數學運算。

三、經典例題

典例1(2019 年浙江卷)祖暅是我國南北朝時期的偉大科學家,他提出的 “冪勢既同,則積不容異”成為祖暅原理,利用該原理可以得到柱體的體積公式V柱體=Sh,其中S是柱體的底面積,h是柱體的高,若某柱體的三視圖如圖1 所示(單位:cm),則該柱體的體積(單 位:cm3)是( )。

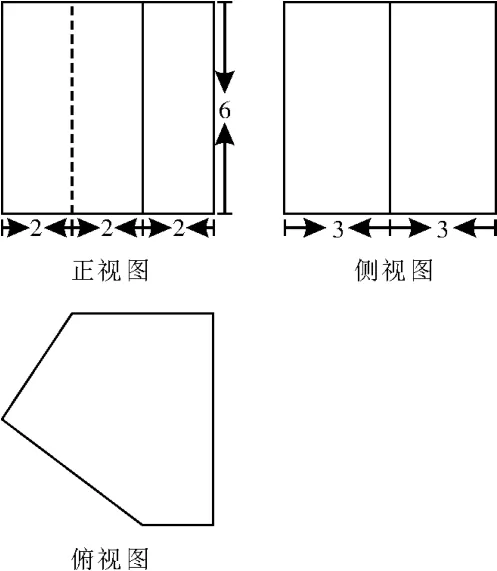
圖1

A.158

B.162

C.182

D.324

解析:由三視圖可知,該幾何體是一個直五棱柱,由正視圖與側視圖可知俯視圖(五邊形)的參數,即3+2×3+6×6)=27(cm2)。又柱體的高為6 cm,所 以 其 體 積V=Sh= 27 × 6 =162(cm3)。故選B。

點評:三視圖問題的常見類型及解題策略:(1)由幾何體的三視圖還原幾何體的形狀,要熟悉柱、錐、臺、球的三視圖,明確三視圖的形成原理,結合空間想象將三視圖還原為實物圖。(2)由幾何體的直觀圖求三視圖。注意正視圖、側視圖和俯視圖的觀察方向,注意看到的部分用實線表示,不能看到的部分用虛線表示。(3)由幾何體的部分視圖畫出剩余的部分視圖。先根據已知的一部分三視圖,還原、推測直觀圖的可能形式,然后再找其剩下部分三視圖的可能形式。

典例2(2019年洛陽第二次統考)在四面體ABCD中,AD⊥平面ABC,AB=,BC=2,若四面體ABCD的外接球的表面積為則四面體ABCD的體積為( )。

A.24 B.12 C.8 D.4

解析:如圖2,因為四面體ABCD的外接球的表面積為所以球的半徑為又AB=AC=BC=2,所以cos∠BAC所以sin∠BAC=所以△ABC的外接圓的直徑為所以O1A=所以球心O到平面ABC的距離OO1=4。又AD⊥平面ABC,所以AD=2OO1=8,所以四面體ABCD的體積為故選C。

圖2

點評:(1)解決與球有關的內切或外接的問題時,關鍵是確定球心的位置,若求內切問題,則球心到各面的距離相等且都為球的半徑;若求外接問題,則球心到各個頂點的距離相等且都為球的半徑,同時要構造出球心到截面圓的垂線段,小圓的半徑和球半徑組成的直角三角形,從而利用解直角三角形求出待求量。(2)熟記正方體、長方體、正四面體的內切(外接)球的半徑對解答客觀題是有很大幫助的。

典例3(2018年全國Ⅰ卷)如圖3,四邊形ABCD為正方形,E,F分別為AD,BC的 中 點,以DF為折痕把△DFC折起,使點C到達點P的位置,且PF⊥BF。

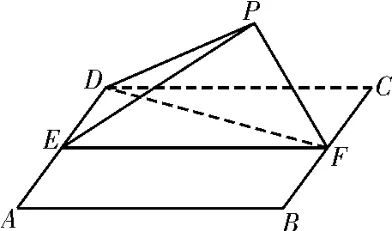
圖3

(1)證明:平面PEF⊥平面ABFD;

(2)求DP與平面ABFD所成角的正弦值。

解析:(1)由已知可得,BF⊥PF,BF⊥EF,所 以BF⊥ 平 面PEF。 又BF? 平 面ABFD,所以平面PEF⊥平面ABFD。

圖4

(2)作PH⊥EF,垂足為H,由(1)得,PH⊥平面ABFD,以H為 坐 標 原 點的方向為y軸正方向,為單位長,建立如圖4 所示的空間直角坐標系H-xyz。由(1)可得,DE⊥PE,又DP=2,DE=1,所以又PF=1,EF=2,故PE⊥PF,可得則H(0,0,0),為平面ABFD的法向量。設DP與平面ABFD所成角為θ,則所以DP與平面ABFD所成角的正弦值為

點評:(1)平行、垂直關系的證明問題是以空間幾何體(主要以柱體和錐體)為載體,通過空間平行、垂直關系的證明進行命題,主要考查公理4及線面(面面)間的平行與垂直的判定或性質定理,常與平面圖形的有關性質進行交匯考查。(2)求線面角時,應注意點的坐標的求解的準確性及公式中角的范圍為

典例4(2019 年全國Ⅲ卷)圖5 是由矩形ADEB、Rt△ABC和菱形BFGC組成的一個平面圖形,其中AB=1,BE=BF=2,∠FBC=60°,將其沿AB,BC折起使得BE與BF重合,連接DG,如圖6。

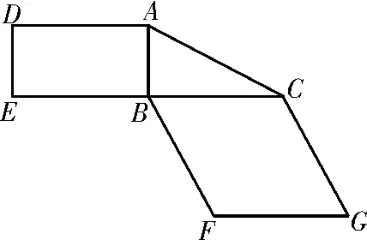
圖5

(1)證明:圖6 中的A,C,G,D四點共面,且平面ABC⊥平面BCGE;

圖6

(2)求圖6中的二面角B-CG-A的大小。

解析:(1)由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG確定一個平面,從而A,C,G,D四點共面。 由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE。又因為AB?平面ABC,所以平面ABC⊥平面BCGE。

(2)作EH⊥BC,垂足為H,因為EH?平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC。由已知得菱形BCGE的邊長為2,∠EBC=60°,可求得BH=1,EH=以H為坐標原點的方向為x軸正方向,建立如圖7所示的空間直角坐標系H-xyz,則A(-1,1,0),C(1,0,0),G設平面ACGD的法向量為n= (x,y,z),則即所以可取n=(3,6,-又平面BCGE的法向量可取為m=(0,1,0),所以因此二面角B-CG-A的大小為30°。

圖7

點評:(1)對于折疊問題,關鍵是理清折疊前后變與不變的數量關系及位置關系,特別是隱含著的垂直關系。(2)建系時,無明顯的垂直關系需要給予證明。

典例5(2019年濟南市高三模擬)如圖8,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥底面ABCD,PA=AB=2,M為 棱PC的中點,E,F分別為棱AB,BC上的動點(E,F與 所在棱的端點不重合),且滿足BE=BF。

圖8

(1)證明:平面PEF⊥平面MBD;

(2)當三棱錐F-PEC的體積最大時,求二面角C-MF-E的余弦值。

解析:(1)連接AC交BD于N,連接MN。因為底面ABCD為正方形,所以AC⊥BD,AN=CN。又PM=MC,所以MN∥PA。又PA⊥底面ABCD,所以MN⊥底面ABCD。又AC?底面ABCD,所以AC⊥MN。又BD∩MN=N,BD,MN?平面MBD,所以AC⊥平面MBD。 因為BE=BF,BA=BC,所以即EF∥AC,所以EF⊥平面MBD。又EF?平面PEF,所以平面PEF⊥平面MBD。

(2)設BE=BF=x,由題意知,S△CEF=又PA=2,所 以V三棱錐F-PEC=易知當三棱錐F-PEC的體積最大時,x=1,即此時E,F分別為棱AB,BC的中點。

以A為坐標原點,的方向為x軸正方向,建立如圖9 所示的空間直角坐標系A-xyz,則C(2,2,0),F(2,1,0),E(1,0,0),M(1,1,1設n=(x1,y1,z1)是平面MEF的法向量,則可取n=(1,-1,1)。設m=(x2,y2,z2)是平面MCF的法向量,則即可取m= (1,0,1),則由圖知所求二面角為鈍二面角,所以二面角C-MF-E的余弦值為

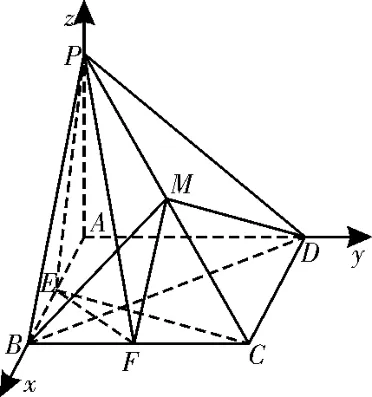
圖9

點評:二面角的求解策略:(1)向量法,又有兩種求法:①分別求出二面角的兩個半平面所在平面的法向量,利用其法向量的夾角并結合實際圖形或法向量的方向確定其二面角的大小。②分別在二面角的兩個半平面內找到與棱垂直且以垂足為起點的兩個向量,顯然這兩個向量的夾角的大小就是二面角的大小。(2)綜合法,根據定義,在圖中指(作)出,并給予證明,然后將其納入可解三角形中求解。